David Saxton
Analysing Mathematical Reasoning Abilities of Neural Models
Apr 02, 2019



Abstract:Mathematical reasoning---a core ability within human intelligence---presents some unique challenges as a domain: we do not come to understand and solve mathematical problems primarily on the back of experience and evidence, but on the basis of inferring, learning, and exploiting laws, axioms, and symbol manipulation rules. In this paper, we present a new challenge for the evaluation (and eventually the design) of neural architectures and similar system, developing a task suite of mathematics problems involving sequential questions and answers in a free-form textual input/output format. The structured nature of the mathematics domain, covering arithmetic, algebra, probability and calculus, enables the construction of training and test splits designed to clearly illuminate the capabilities and failure-modes of different architectures, as well as evaluate their ability to compose and relate knowledge and learned processes. Having described the data generation process and its potential future expansions, we conduct a comprehensive analysis of models from two broad classes of the most powerful sequence-to-sequence architectures and find notable differences in their ability to resolve mathematical problems and generalize their knowledge.
Meta-Learning surrogate models for sequential decision making
Mar 28, 2019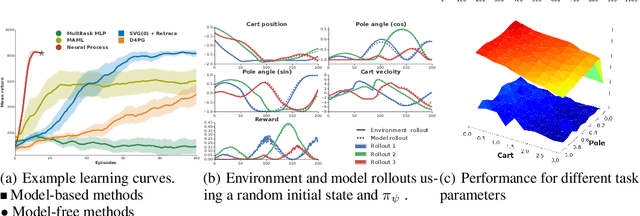

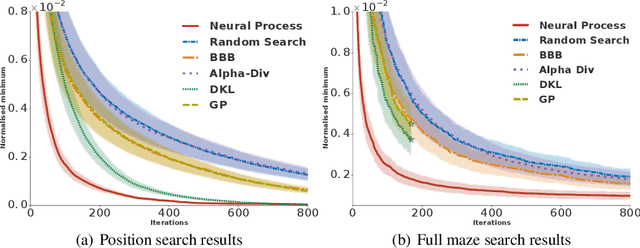
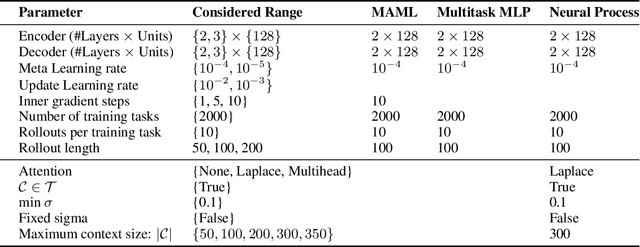
Abstract:Meta-learning methods leverage past experience to learn data-driven inductive biases from related problems, increasing learning efficiency on new tasks. This ability renders them particularly suitable for sequential decision making with limited experience. Within this problem family, we argue for the use of such approaches in the study of model-based approaches to Bayesian Optimisation, contextual bandits and Reinforcement Learning. We approach the problem by learning distributions over functions using Neural Processes (NPs), a recently introduced probabilistic meta-learning method. This allows the treatment of model uncertainty to tackle the exploration/exploitation dilemma. We show that NPs are suitable for sequential decision making on a diverse set of domains, including adversarial task search, recommender systems and model-based reinforcement learning.
Conditional Neural Processes
Jul 04, 2018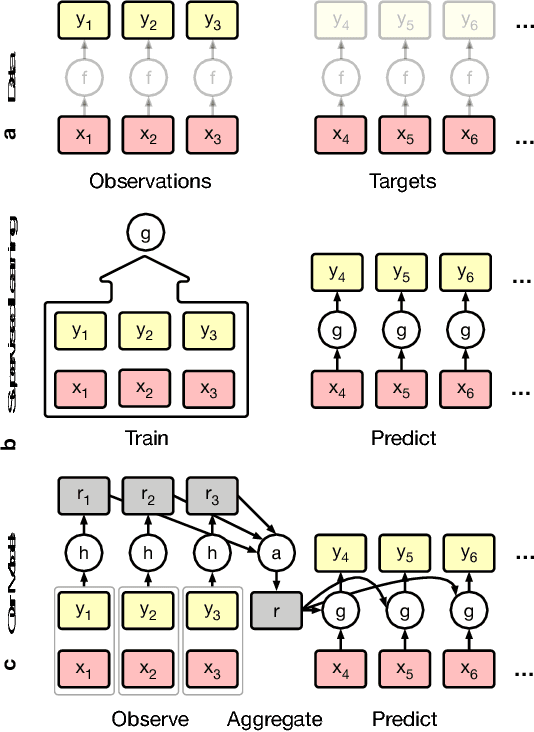
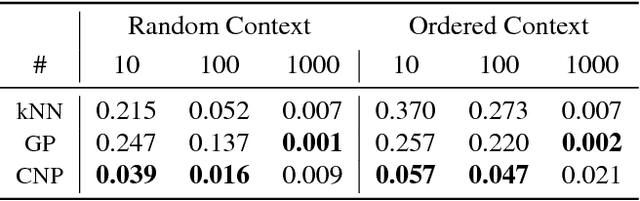
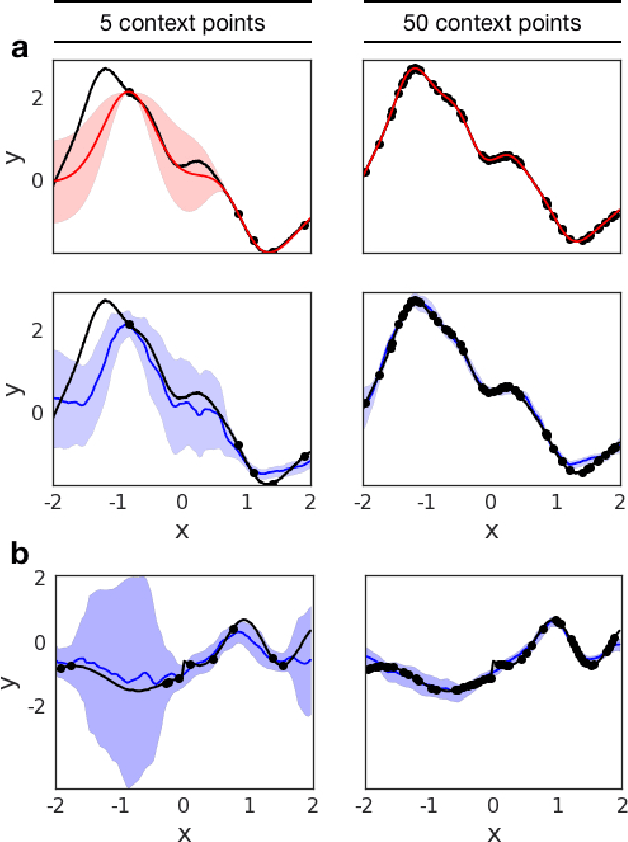
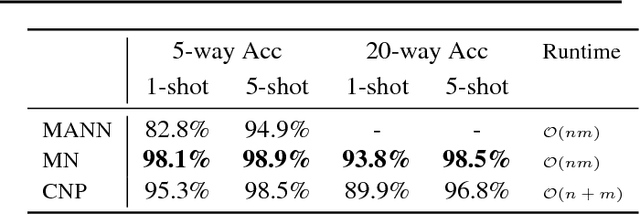
Abstract:Deep neural networks excel at function approximation, yet they are typically trained from scratch for each new function. On the other hand, Bayesian methods, such as Gaussian Processes (GPs), exploit prior knowledge to quickly infer the shape of a new function at test time. Yet GPs are computationally expensive, and it can be hard to design appropriate priors. In this paper we propose a family of neural models, Conditional Neural Processes (CNPs), that combine the benefits of both. CNPs are inspired by the flexibility of stochastic processes such as GPs, but are structured as neural networks and trained via gradient descent. CNPs make accurate predictions after observing only a handful of training data points, yet scale to complex functions and large datasets. We demonstrate the performance and versatility of the approach on a range of canonical machine learning tasks, including regression, classification and image completion.
Unsupervised Predictive Memory in a Goal-Directed Agent
Mar 28, 2018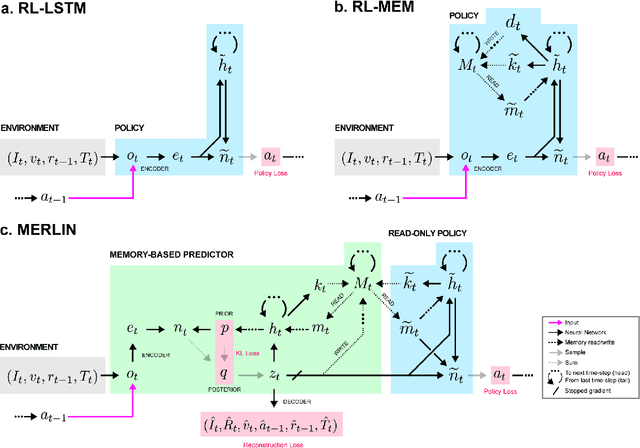
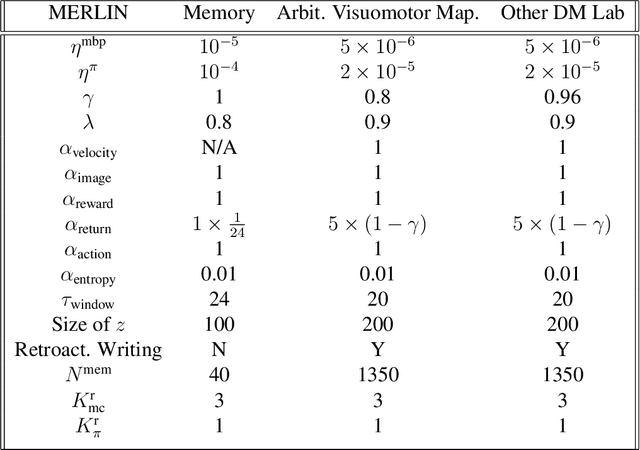
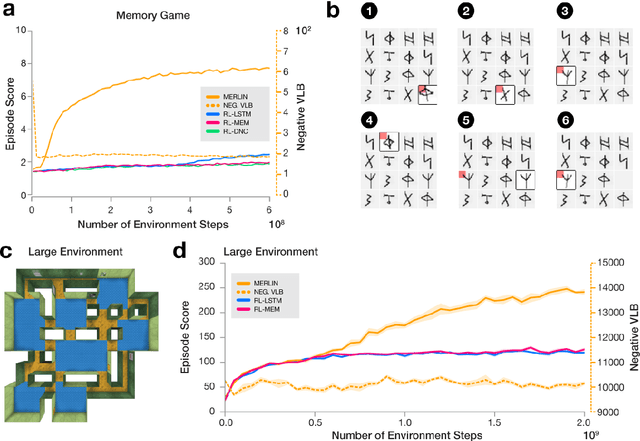

Abstract:Animals execute goal-directed behaviours despite the limited range and scope of their sensors. To cope, they explore environments and store memories maintaining estimates of important information that is not presently available. Recently, progress has been made with artificial intelligence (AI) agents that learn to perform tasks from sensory input, even at a human level, by merging reinforcement learning (RL) algorithms with deep neural networks, and the excitement surrounding these results has led to the pursuit of related ideas as explanations of non-human animal learning. However, we demonstrate that contemporary RL algorithms struggle to solve simple tasks when enough information is concealed from the sensors of the agent, a property called "partial observability". An obvious requirement for handling partially observed tasks is access to extensive memory, but we show memory is not enough; it is critical that the right information be stored in the right format. We develop a model, the Memory, RL, and Inference Network (MERLIN), in which memory formation is guided by a process of predictive modeling. MERLIN facilitates the solution of tasks in 3D virtual reality environments for which partial observability is severe and memories must be maintained over long durations. Our model demonstrates a single learning agent architecture that can solve canonical behavioural tasks in psychology and neurobiology without strong simplifying assumptions about the dimensionality of sensory input or the duration of experiences.
Can Neural Networks Understand Logical Entailment?
Feb 23, 2018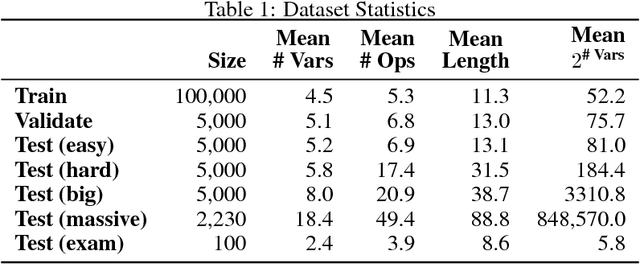
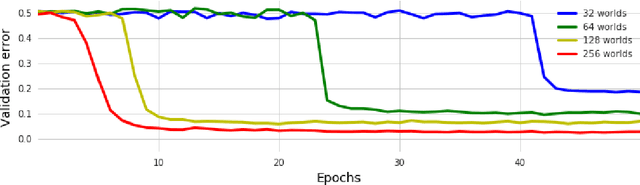
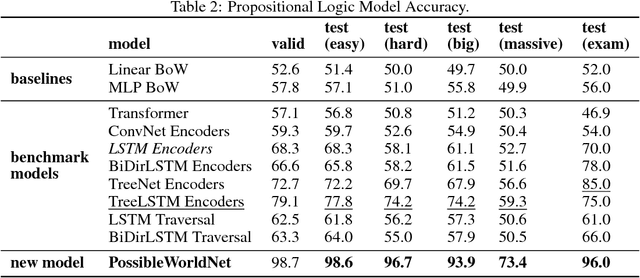
Abstract:We introduce a new dataset of logical entailments for the purpose of measuring models' ability to capture and exploit the structure of logical expressions against an entailment prediction task. We use this task to compare a series of architectures which are ubiquitous in the sequence-processing literature, in addition to a new model class---PossibleWorldNets---which computes entailment as a "convolution over possible worlds". Results show that convolutional networks present the wrong inductive bias for this class of problems relative to LSTM RNNs, tree-structured neural networks outperform LSTM RNNs due to their enhanced ability to exploit the syntax of logic, and PossibleWorldNets outperform all benchmarks.
Programmable Agents
Jun 20, 2017



Abstract:We build deep RL agents that execute declarative programs expressed in formal language. The agents learn to ground the terms in this language in their environment, and can generalize their behavior at test time to execute new programs that refer to objects that were not referenced during training. The agents develop disentangled interpretable representations that allow them to generalize to a wide variety of zero-shot semantic tasks.
Unifying Count-Based Exploration and Intrinsic Motivation
Nov 07, 2016



Abstract:We consider an agent's uncertainty about its environment and the problem of generalizing this uncertainty across observations. Specifically, we focus on the problem of exploration in non-tabular reinforcement learning. Drawing inspiration from the intrinsic motivation literature, we use density models to measure uncertainty, and propose a novel algorithm for deriving a pseudo-count from an arbitrary density model. This technique enables us to generalize count-based exploration algorithms to the non-tabular case. We apply our ideas to Atari 2600 games, providing sensible pseudo-counts from raw pixels. We transform these pseudo-counts into intrinsic rewards and obtain significantly improved exploration in a number of hard games, including the infamously difficult Montezuma's Revenge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge