Bad Students Make Great Teachers: Active Learning Accelerates Large-Scale Visual Understanding

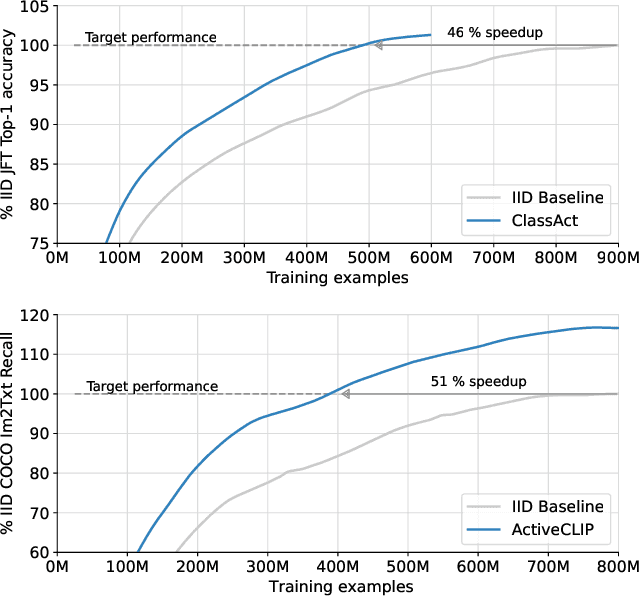
We propose a method for accelerating large-scale pre-training with online data selection policies. For the first time, we demonstrate that model-based data selection can reduce the total computation needed to reach the performance of models trained with uniform sampling. The key insight which enables this "compute-positive" regime is that small models provide good proxies for the loss of much larger models, such that computation spent on scoring data can be drastically scaled down but still significantly accelerate training of the learner.. These data selection policies also strongly generalize across datasets and tasks, opening an avenue for further amortizing the overhead of data scoring by re-using off-the-shelf models and training sequences. Our methods, ClassAct and ActiveCLIP, require 46% and 51% fewer training updates and up to 25% less total computation when training visual classifiers on JFT and multimodal models on ALIGN, respectively. Finally, our paradigm seamlessly applies to the curation of large-scale image-text datasets, yielding a new state-of-the-art in several multimodal transfer tasks and pre-training regimes.

Quantum State Assignment Flows

This paper introduces assignment flows for density matrices as state spaces for representing and analyzing data associated with vertices of an underlying weighted graph. Determining an assignment flow by geometric integration of the defining dynamical system causes an interaction of the non-commuting states across the graph, and the assignment of a pure (rank-one) state to each vertex after convergence. Adopting the Riemannian Bogoliubov-Kubo-Mori metric from information geometry leads to closed-form local expressions which can be computed efficiently and implemented in a fine-grained parallel manner. Restriction to the submanifold of commuting density matrices recovers the assignment flows for categorial probability distributions, which merely assign labels from a finite set to each data point. As shown for these flows in our prior work, the novel class of quantum state assignment flows can also be characterized as Riemannian gradient flows with respect to a non-local non-convex potential, after proper reparametrization and under mild conditions on the underlying weight function. This weight function generates the parameters of the layers of a neural network, corresponding to and generated by each step of the geometric integration scheme. Numerical results indicates and illustrate the potential of the novel approach for data representation and analysis, including the representation of correlations of data across the graph by entanglement and tensorization.

Powerpropagation: A sparsity inducing weight reparameterisation

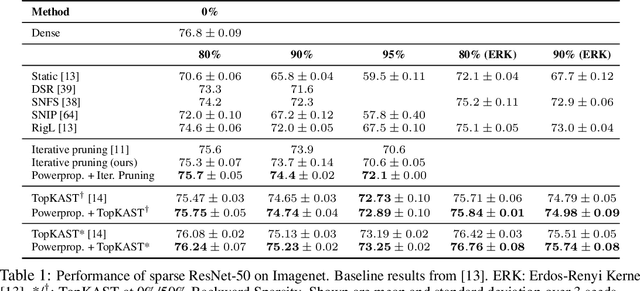
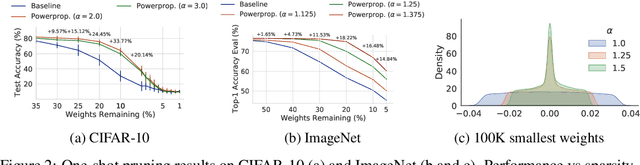
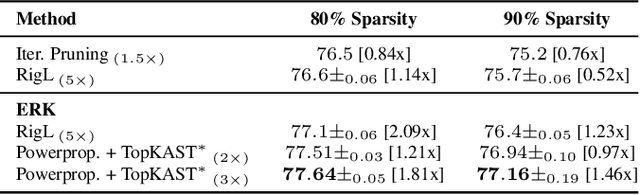
The training of sparse neural networks is becoming an increasingly important tool for reducing the computational footprint of models at training and evaluation, as well enabling the effective scaling up of models. Whereas much work over the years has been dedicated to specialised pruning techniques, little attention has been paid to the inherent effect of gradient based training on model sparsity. In this work, we introduce Powerpropagation, a new weight-parameterisation for neural networks that leads to inherently sparse models. Exploiting the behaviour of gradient descent, our method gives rise to weight updates exhibiting a "rich get richer" dynamic, leaving low-magnitude parameters largely unaffected by learning. Models trained in this manner exhibit similar performance, but have a distribution with markedly higher density at zero, allowing more parameters to be pruned safely. Powerpropagation is general, intuitive, cheap and straight-forward to implement and can readily be combined with various other techniques. To highlight its versatility, we explore it in two very different settings: Firstly, following a recent line of work, we investigate its effect on sparse training for resource-constrained settings. Here, we combine Powerpropagation with a traditional weight-pruning technique as well as recent state-of-the-art sparse-to-sparse algorithms, showing superior performance on the ImageNet benchmark. Secondly, we advocate the use of sparsity in overcoming catastrophic forgetting, where compressed representations allow accommodating a large number of tasks at fixed model capacity. In all cases our reparameterisation considerably increases the efficacy of the off-the-shelf methods.

Behavior Priors for Efficient Reinforcement Learning

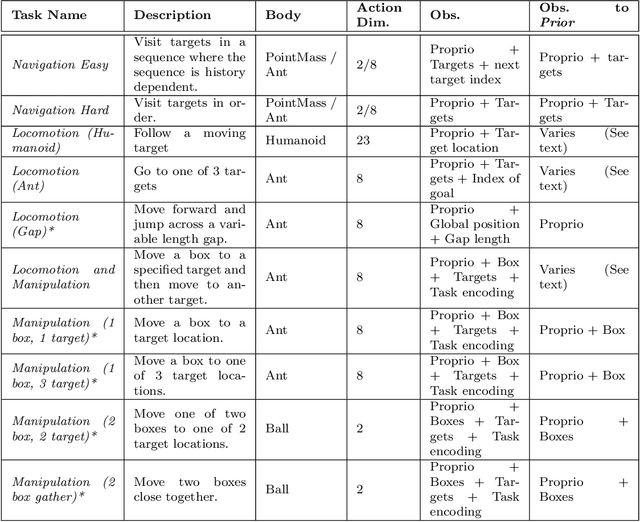
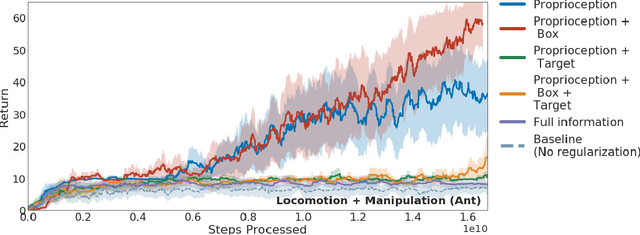
As we deploy reinforcement learning agents to solve increasingly challenging problems, methods that allow us to inject prior knowledge about the structure of the world and effective solution strategies becomes increasingly important. In this work we consider how information and architectural constraints can be combined with ideas from the probabilistic modeling literature to learn behavior priors that capture the common movement and interaction patterns that are shared across a set of related tasks or contexts. For example the day-to day behavior of humans comprises distinctive locomotion and manipulation patterns that recur across many different situations and goals. We discuss how such behavior patterns can be captured using probabilistic trajectory models and how these can be integrated effectively into reinforcement learning schemes, e.g.\ to facilitate multi-task and transfer learning. We then extend these ideas to latent variable models and consider a formulation to learn hierarchical priors that capture different aspects of the behavior in reusable modules. We discuss how such latent variable formulations connect to related work on hierarchical reinforcement learning (HRL) and mutual information and curiosity based objectives, thereby offering an alternative perspective on existing ideas. We demonstrate the effectiveness of our framework by applying it to a range of simulated continuous control domains.

Information asymmetry in KL-regularized RL

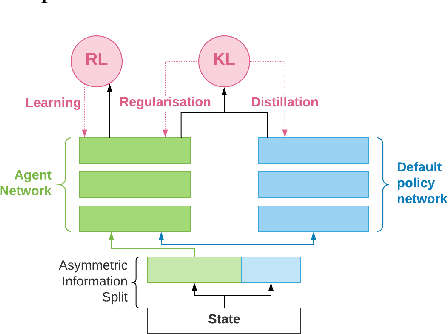
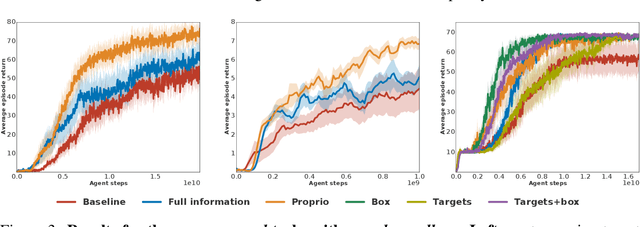
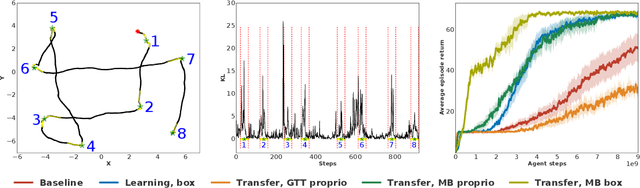
Many real world tasks exhibit rich structure that is repeated across different parts of the state space or in time. In this work we study the possibility of leveraging such repeated structure to speed up and regularize learning. We start from the KL regularized expected reward objective which introduces an additional component, a default policy. Instead of relying on a fixed default policy, we learn it from data. But crucially, we restrict the amount of information the default policy receives, forcing it to learn reusable behaviors that help the policy learn faster. We formalize this strategy and discuss connections to information bottleneck approaches and to the variational EM algorithm. We present empirical results in both discrete and continuous action domains and demonstrate that, for certain tasks, learning a default policy alongside the policy can significantly speed up and improve learning.

Meta-Learning surrogate models for sequential decision making

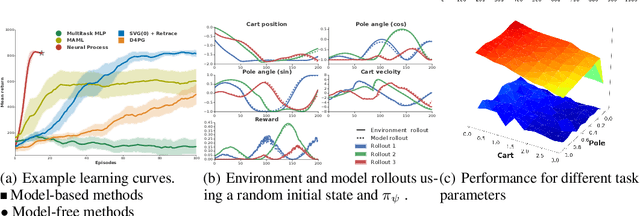
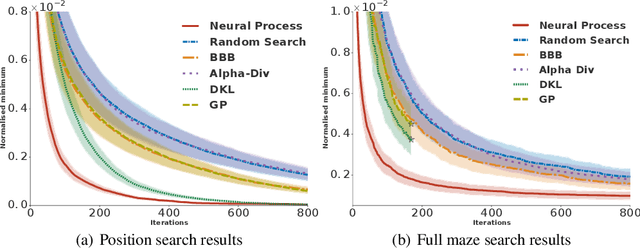
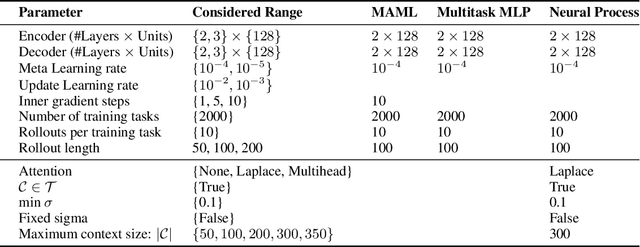
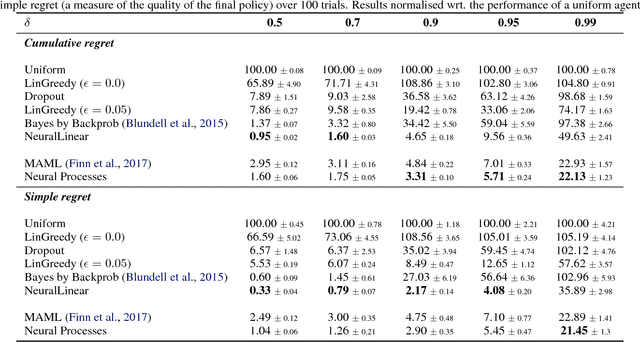
Meta-learning methods leverage past experience to learn data-driven inductive biases from related problems, increasing learning efficiency on new tasks. This ability renders them particularly suitable for sequential decision making with limited experience. Within this problem family, we argue for the use of such approaches in the study of model-based approaches to Bayesian Optimisation, contextual bandits and Reinforcement Learning. We approach the problem by learning distributions over functions using Neural Processes (NPs), a recently introduced probabilistic meta-learning method. This allows the treatment of model uncertainty to tackle the exploration/exploitation dilemma. We show that NPs are suitable for sequential decision making on a diverse set of domains, including adversarial task search, recommender systems and model-based reinforcement learning.

Functional Regularisation for Continual Learning using Gaussian Processes

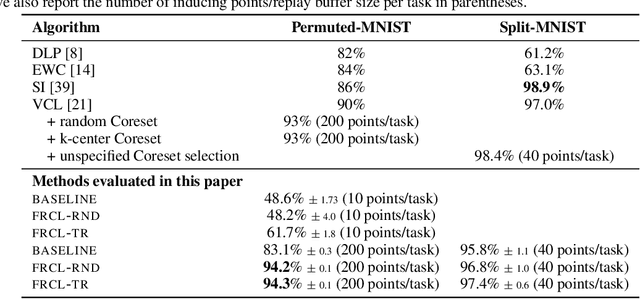
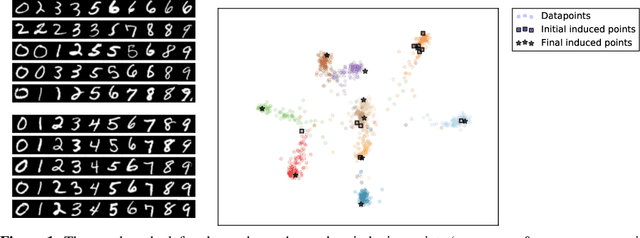
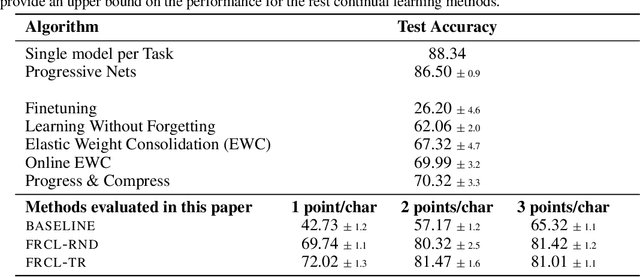
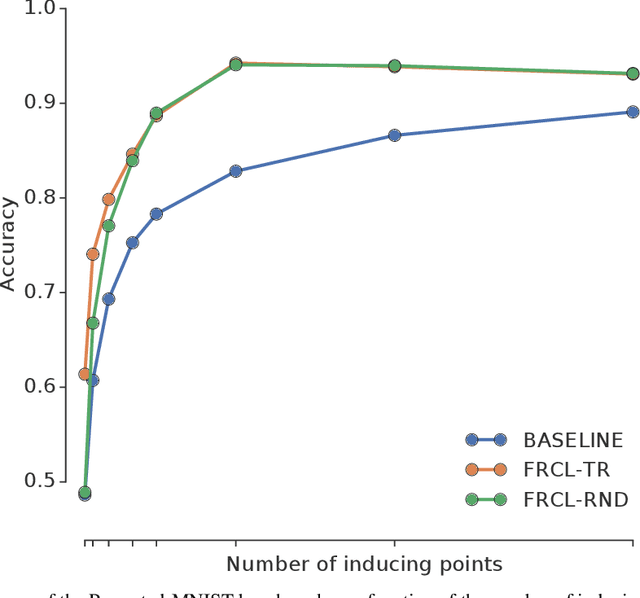
We introduce a novel approach for supervised continual learning based on approximate Bayesian inference over function space rather than the parameters of a deep neural network. We use a Gaussian process obtained by treating the weights of the last layer of a neural network as random and Gaussian distributed. Functional regularisation for continual learning naturally arises by applying the variational sparse GP inference method in a sequential fashion as new tasks are encountered. At each step of the process, a summary is constructed for the current task that consists of (i) inducing inputs and (ii) a posterior distribution over the function values at these inputs. This summary then regularises learning of future tasks, through Kullback-Leibler regularisation terms that appear in the variational lower bound, and reduces the effects of catastrophic forgetting. We fully develop the theory of the method and we demonstrate its effectiveness in classification datasets, such as Split-MNIST, Permuted-MNIST and Omniglot.

Attentive Neural Processes

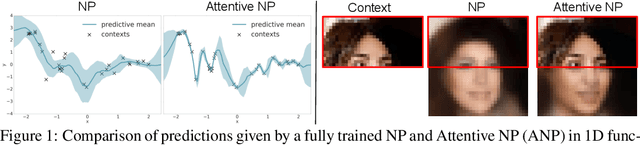
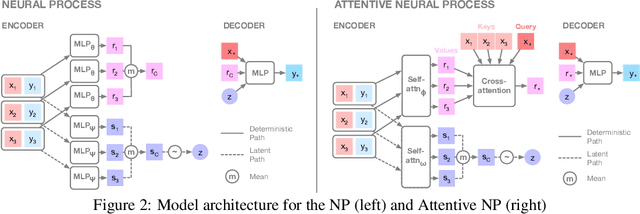
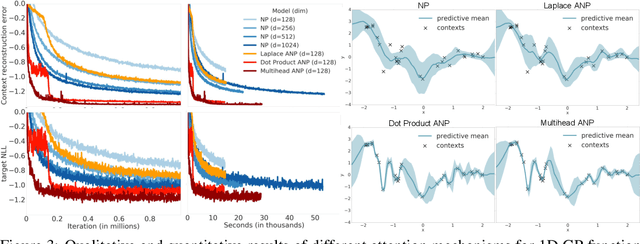
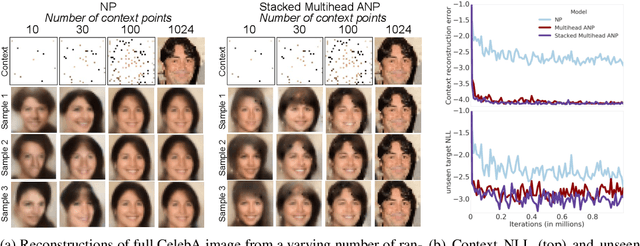
Neural Processes (NPs) (Garnelo et al 2018a;b) approach regression by learning to map a context set of observed input-output pairs to a distribution over regression functions. Each function models the distribution of the output given an input, conditioned on the context. NPs have the benefit of fitting observed data efficiently with linear complexity in the number of context input-output pairs, and can learn a wide family of conditional distributions; they learn predictive distributions conditioned on context sets of arbitrary size. Nonetheless, we show that NPs suffer a fundamental drawback of underfitting, giving inaccurate predictions at the inputs of the observed data they condition on. We address this issue by incorporating attention into NPs, allowing each input location to attend to the relevant context points for the prediction. We show that this greatly improves the accuracy of predictions, results in noticeably faster training, and expands the range of functions that can be modelled.

Experience Replay for Continual Learning

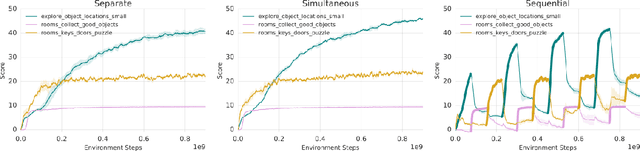
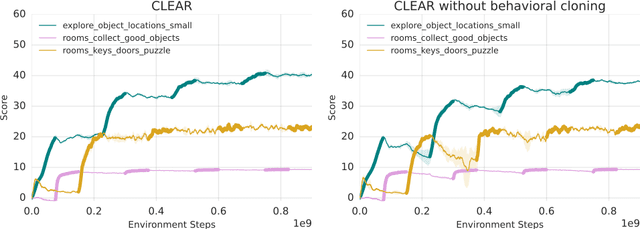
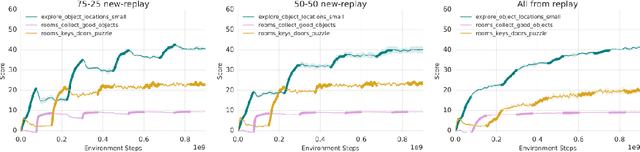
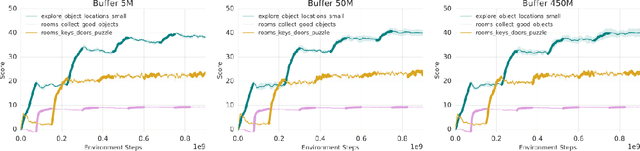
Continual learning is the problem of learning new tasks or knowledge while protecting old knowledge and ideally generalizing from old experience to learn new tasks faster. Neural networks trained by stochastic gradient descent often degrade on old tasks when trained successively on new tasks with different data distributions. This phenomenon, referred to as catastrophic forgetting, is considered a major hurdle to learning with non-stationary data or sequences of new tasks, and prevents networks from continually accumulating knowledge and skills. We examine this issue in the context of reinforcement learning, in a setting where an agent is exposed to tasks in a sequence. Unlike most other work, we do not provide an explicit indication to the model of task boundaries, which is the most general circumstance for a learning agent exposed to continuous experience. While various methods to counteract catastrophic forgetting have recently been proposed, we explore a straightforward, general, and seemingly overlooked solution - that of using experience replay buffers for all past events - with a mixture of on- and off-policy learning, leveraging behavioral cloning. We show that this strategy can still learn new tasks quickly yet can substantially reduce catastrophic forgetting in both Atari and DMLab domains, even matching the performance of methods that require task identities. When buffer storage is constrained, we confirm that a simple mechanism for randomly discarding data allows a limited size buffer to perform almost as well as an unbounded one.

Neural Processes

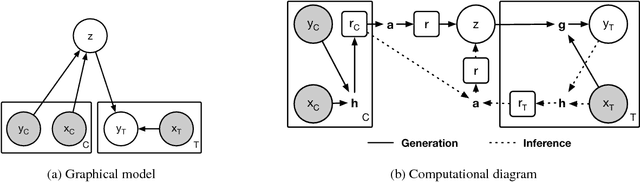
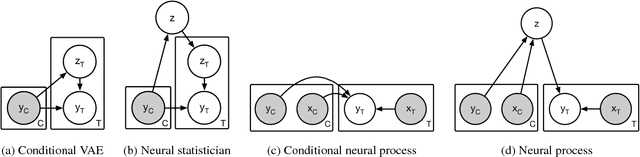
A neural network (NN) is a parameterised function that can be tuned via gradient descent to approximate a labelled collection of data with high precision. A Gaussian process (GP), on the other hand, is a probabilistic model that defines a distribution over possible functions, and is updated in light of data via the rules of probabilistic inference. GPs are probabilistic, data-efficient and flexible, however they are also computationally intensive and thus limited in their applicability. We introduce a class of neural latent variable models which we call Neural Processes (NPs), combining the best of both worlds. Like GPs, NPs define distributions over functions, are capable of rapid adaptation to new observations, and can estimate the uncertainty in their predictions. Like NNs, NPs are computationally efficient during training and evaluation but also learn to adapt their priors to data. We demonstrate the performance of NPs on a range of learning tasks, including regression and optimisation, and compare and contrast with related models in the literature.