Optimal Learning Rate Schedule for Balancing Effort and Performance

Learning how to learn efficiently is a fundamental challenge for biological agents and a growing concern for artificial ones. To learn effectively, an agent must regulate its learning speed, balancing the benefits of rapid improvement against the costs of effort, instability, or resource use. We introduce a normative framework that formalizes this problem as an optimal control process in which the agent maximizes cumulative performance while incurring a cost of learning. From this objective, we derive a closed-form solution for the optimal learning rate, which has the form of a closed-loop controller that depends only on the agent's current and expected future performance. Under mild assumptions, this solution generalizes across tasks and architectures and reproduces numerically optimized schedules in simulations. In simple learning models, we can mathematically analyze how agent and task parameters shape learning-rate scheduling as an open-loop control solution. Because the optimal policy depends on expectations of future performance, the framework predicts how overconfidence or underconfidence influence engagement and persistence, linking the control of learning speed to theories of self-regulated learning. We further show how a simple episodic memory mechanism can approximate the required performance expectations by recalling similar past learning experiences, providing a biologically plausible route to near-optimal behaviour. Together, these results provide a normative and biologically plausible account of learning speed control, linking self-regulated learning, effort allocation, and episodic memory estimation within a unified and tractable mathematical framework.

Saddle-to-Saddle Dynamics Explains A Simplicity Bias Across Neural Network Architectures

Neural networks trained with gradient descent often learn solutions of increasing complexity over time, a phenomenon known as simplicity bias. Despite being widely observed across architectures, existing theoretical treatments lack a unifying framework. We present a theoretical framework that explains a simplicity bias arising from saddle-to-saddle learning dynamics for a general class of neural networks, incorporating fully-connected, convolutional, and attention-based architectures. Here, simple means expressible with few hidden units, i.e., hidden neurons, convolutional kernels, or attention heads. Specifically, we show that linear networks learn solutions of increasing rank, ReLU networks learn solutions with an increasing number of kinks, convolutional networks learn solutions with an increasing number of convolutional kernels, and self-attention models learn solutions with an increasing number of attention heads. By analyzing fixed points, invariant manifolds, and dynamics of gradient descent learning, we show that saddle-to-saddle dynamics operates by iteratively evolving near an invariant manifold, approaching a saddle, and switching to another invariant manifold. Our analysis also illuminates the effects of data distribution and weight initialization on the duration and number of plateaus in learning, dissociating previously confounding factors. Overall, our theory offers a framework for understanding when and why gradient descent progressively learns increasingly complex solutions.

Training Dynamics of In-Context Learning in Linear Attention

While attention-based models have demonstrated the remarkable ability of in-context learning, the theoretical understanding of how these models acquired this ability through gradient descent training is still preliminary. Towards answering this question, we study the gradient descent dynamics of multi-head linear self-attention trained for in-context linear regression. We examine two parametrizations of linear self-attention: one with the key and query weights merged as a single matrix (common in theoretical studies), and one with separate key and query matrices (closer to practical settings). For the merged parametrization, we show the training dynamics has two fixed points and the loss trajectory exhibits a single, abrupt drop. We derive an analytical time-course solution for a certain class of datasets and initialization. For the separate parametrization, we show the training dynamics has exponentially many fixed points and the loss exhibits saddle-to-saddle dynamics, which we reduce to scalar ordinary differential equations. During training, the model implements principal component regression in context with the number of principal components increasing over training time. Overall, we characterize how in-context learning abilities evolve during gradient descent training of linear attention, revealing dynamics of abrupt acquisition versus progressive improvements in models with different parametrizations.

When Are Bias-Free ReLU Networks Like Linear Networks?

We investigate the expressivity and learning dynamics of bias-free ReLU networks. We firstly show that two-layer bias-free ReLU networks have limited expressivity: the only odd function two-layer bias-free ReLU networks can express is a linear one. We then show that, under symmetry conditions on the data, these networks have the same learning dynamics as linear networks. This allows us to give closed-form time-course solutions to certain two-layer bias-free ReLU networks, which has not been done for nonlinear networks outside the lazy learning regime. While deep bias-free ReLU networks are more expressive than their two-layer counterparts, they still share a number of similarities with deep linear networks. These similarities enable us to leverage insights from linear networks, leading to a novel understanding of bias-free ReLU networks. Overall, our results show that some properties established for bias-free ReLU networks arise due to equivalence to linear networks, and suggest that including bias or considering asymmetric data are avenues to engage with nonlinear behaviors.

A Theory of Unimodal Bias in Multimodal Learning

Using multiple input streams simultaneously in training multimodal neural networks is intuitively advantageous, but practically challenging. A key challenge is unimodal bias, where a network overly relies on one modality and ignores others during joint training. While unimodal bias is well-documented empirically, our theoretical understanding of how architecture and data statistics influence this bias remains incomplete. Here we develop a theory of unimodal bias with deep multimodal linear networks. We calculate the duration of the unimodal phase in learning as a function of the depth at which modalities are fused within the network, dataset statistics, and initialization. We find that the deeper the layer at which fusion occurs, the longer the unimodal phase. A long unimodal phase can lead to a generalization deficit and permanent unimodal bias in the overparametrized regime. In addition, our theory reveals the modality learned first is not necessarily the modality that contributes more to the output. Our results, derived for multimodal linear networks, extend to ReLU networks in certain settings. Taken together, this work illuminates pathologies of multimodal learning under joint training, showing that late and intermediate fusion architectures can give rise to long unimodal phases and permanent unimodal bias.

Powerpropagation: A sparsity inducing weight reparameterisation

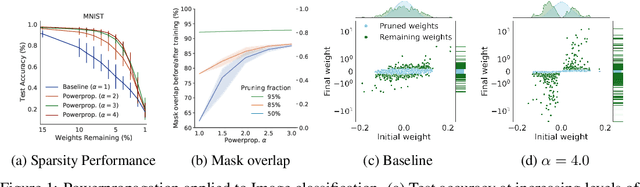
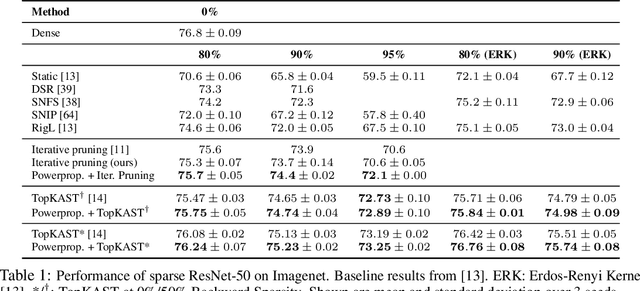
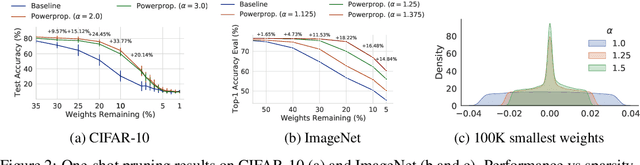
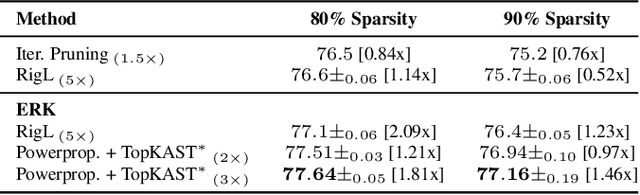
The training of sparse neural networks is becoming an increasingly important tool for reducing the computational footprint of models at training and evaluation, as well enabling the effective scaling up of models. Whereas much work over the years has been dedicated to specialised pruning techniques, little attention has been paid to the inherent effect of gradient based training on model sparsity. In this work, we introduce Powerpropagation, a new weight-parameterisation for neural networks that leads to inherently sparse models. Exploiting the behaviour of gradient descent, our method gives rise to weight updates exhibiting a "rich get richer" dynamic, leaving low-magnitude parameters largely unaffected by learning. Models trained in this manner exhibit similar performance, but have a distribution with markedly higher density at zero, allowing more parameters to be pruned safely. Powerpropagation is general, intuitive, cheap and straight-forward to implement and can readily be combined with various other techniques. To highlight its versatility, we explore it in two very different settings: Firstly, following a recent line of work, we investigate its effect on sparse training for resource-constrained settings. Here, we combine Powerpropagation with a traditional weight-pruning technique as well as recent state-of-the-art sparse-to-sparse algorithms, showing superior performance on the ImageNet benchmark. Secondly, we advocate the use of sparsity in overcoming catastrophic forgetting, where compressed representations allow accommodating a large number of tasks at fixed model capacity. In all cases our reparameterisation considerably increases the efficacy of the off-the-shelf methods.

Towards Biologically Plausible Convolutional Networks

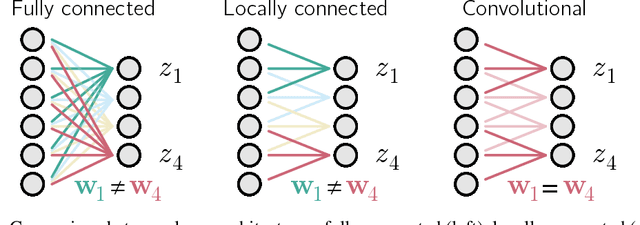
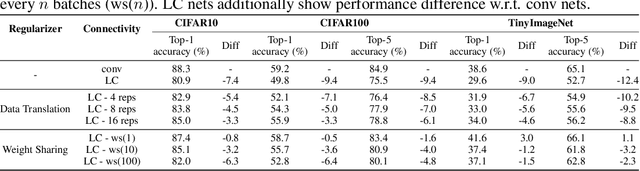
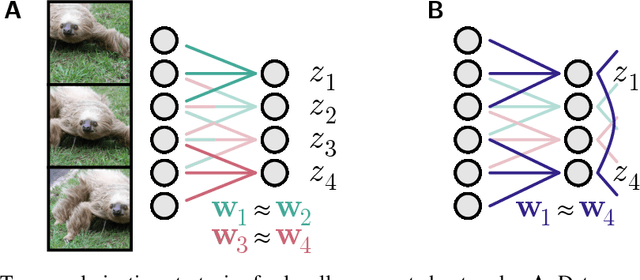
Convolutional networks are ubiquitous in deep learning. They are particularly useful for images, as they reduce the number of parameters, reduce training time, and increase accuracy. However, as a model of the brain they are seriously problematic, since they require weight sharing - something real neurons simply cannot do. Consequently, while neurons in the brain can be locally connected (one of the features of convolutional networks), they cannot be convolutional. Locally connected but non-convolutional networks, however, significantly underperform convolutional ones. This is troublesome for studies that use convolutional networks to explain activity in the visual system. Here we study plausible alternatives to weight sharing that aim at the same regularization principle, which is to make each neuron within a pool react similarly to identical inputs. The most natural way to do that is by showing the network multiple translations of the same image, akin to saccades in animal vision. However, this approach requires many translations, and doesn't remove the performance gap. We propose instead to add lateral connectivity to a locally connected network, and allow learning via Hebbian plasticity. This requires the network to pause occasionally for a sleep-like phase of "weight sharing". This method enables locally connected networks to achieve nearly convolutional performance on ImageNet, thus supporting convolutional networks as a model of the visual stream.

Kernelized information bottleneck leads to biologically plausible 3-factor Hebbian learning in deep networks

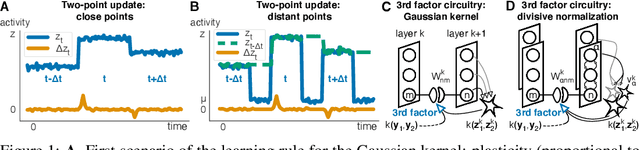
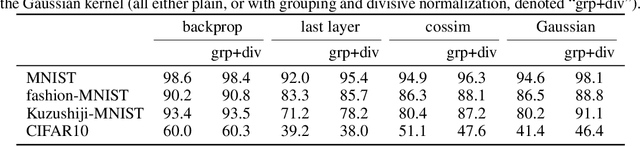
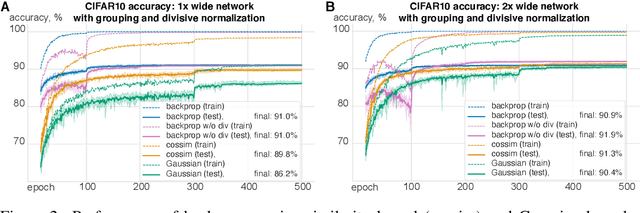
The state-of-the art machine learning approach to training deep neural networks, backpropagation, is implausible for real neural networks: neurons need to know their outgoing weights; training alternates between a forward pass (computation) and a backward pass (learning); and the algorithm needs a large amount of labeled data. Biologically plausible approximations to backpropagation, such as feedback alignment, solve the weight transport problem, but not the other two. Thus, fully biologically plausible learning rules have so far remained elusive. Here we present a family of learning rules that does not suffer from any of these problems. It is motivated by the information bottleneck principle (extended with kernel methods), in which networks learn to squeeze as much information as possible out of the input without sacrificing prediction of the output. The resulting rules have a 3-factor Hebbian structure: they require pre- and post-synaptic firing rates and a global error signal - the third factor - that can be supplied by a neuromodulator. Moreover, they do not require precise labels; instead, they rely on the similarity between the desired outputs. They thus solve all three implausibility issues of backpropagation. Moreover, to obtain good performance on hard problems and retain biologically plausible learning rules, our rules need divisive normalization - a known feature of biological networks. Finally, simulations show that our rule performs nearly as well as backpropagation on image classification tasks.