Kernelized information bottleneck leads to biologically plausible 3-factor Hebbian learning in deep networks

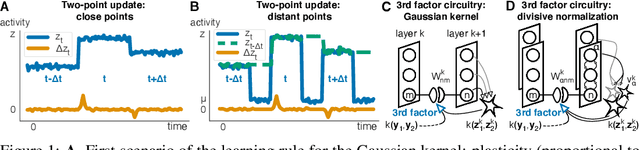
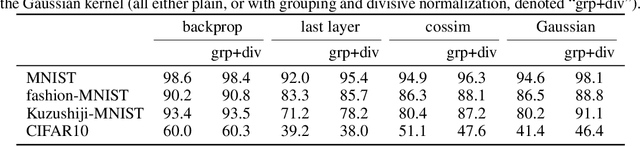
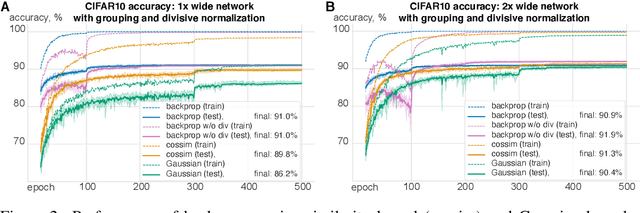
The state-of-the art machine learning approach to training deep neural networks, backpropagation, is implausible for real neural networks: neurons need to know their outgoing weights; training alternates between a forward pass (computation) and a backward pass (learning); and the algorithm needs a large amount of labeled data. Biologically plausible approximations to backpropagation, such as feedback alignment, solve the weight transport problem, but not the other two. Thus, fully biologically plausible learning rules have so far remained elusive. Here we present a family of learning rules that does not suffer from any of these problems. It is motivated by the information bottleneck principle (extended with kernel methods), in which networks learn to squeeze as much information as possible out of the input without sacrificing prediction of the output. The resulting rules have a 3-factor Hebbian structure: they require pre- and post-synaptic firing rates and a global error signal - the third factor - that can be supplied by a neuromodulator. Moreover, they do not require precise labels; instead, they rely on the similarity between the desired outputs. They thus solve all three implausibility issues of backpropagation. Moreover, to obtain good performance on hard problems and retain biologically plausible learning rules, our rules need divisive normalization - a known feature of biological networks. Finally, simulations show that our rule performs nearly as well as backpropagation on image classification tasks.