Functional Regularisation for Continual Learning using Gaussian Processes

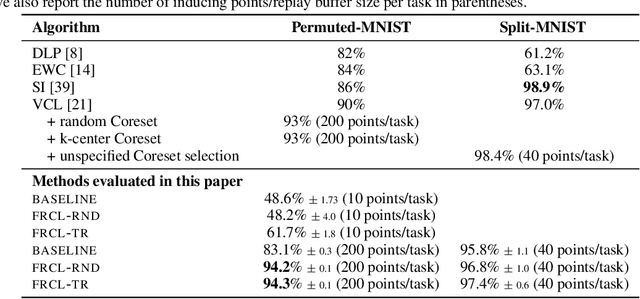
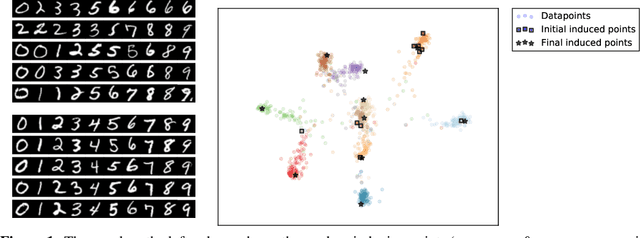
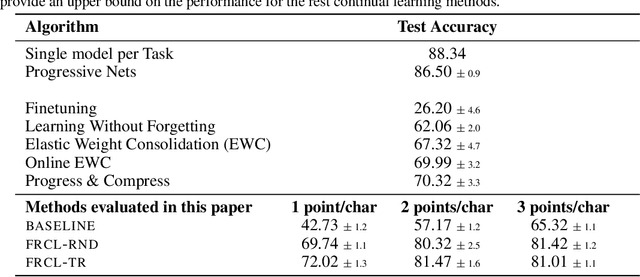
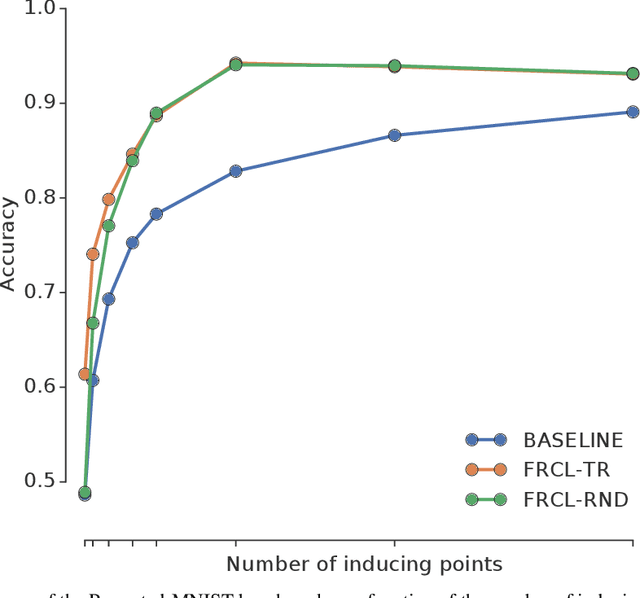
We introduce a novel approach for supervised continual learning based on approximate Bayesian inference over function space rather than the parameters of a deep neural network. We use a Gaussian process obtained by treating the weights of the last layer of a neural network as random and Gaussian distributed. Functional regularisation for continual learning naturally arises by applying the variational sparse GP inference method in a sequential fashion as new tasks are encountered. At each step of the process, a summary is constructed for the current task that consists of (i) inducing inputs and (ii) a posterior distribution over the function values at these inputs. This summary then regularises learning of future tasks, through Kullback-Leibler regularisation terms that appear in the variational lower bound, and reduces the effects of catastrophic forgetting. We fully develop the theory of the method and we demonstrate its effectiveness in classification datasets, such as Split-MNIST, Permuted-MNIST and Omniglot.