Quantum computing and artificial intelligence: status and perspectives

This white paper discusses and explores the various points of intersection between quantum computing and artificial intelligence (AI). It describes how quantum computing could support the development of innovative AI solutions. It also examines use cases of classical AI that can empower research and development in quantum technologies, with a focus on quantum computing and quantum sensing. The purpose of this white paper is to provide a long-term research agenda aimed at addressing foundational questions about how AI and quantum computing interact and benefit one another. It concludes with a set of recommendations and challenges, including how to orchestrate the proposed theoretical work, align quantum AI developments with quantum hardware roadmaps, estimate both classical and quantum resources - especially with the goal of mitigating and optimizing energy consumption - advance this emerging hybrid software engineering discipline, and enhance European industrial competitiveness while considering societal implications.

Quantum State Assignment Flows

This paper introduces assignment flows for density matrices as state spaces for representing and analyzing data associated with vertices of an underlying weighted graph. Determining an assignment flow by geometric integration of the defining dynamical system causes an interaction of the non-commuting states across the graph, and the assignment of a pure (rank-one) state to each vertex after convergence. Adopting the Riemannian Bogoliubov-Kubo-Mori metric from information geometry leads to closed-form local expressions which can be computed efficiently and implemented in a fine-grained parallel manner. Restriction to the submanifold of commuting density matrices recovers the assignment flows for categorial probability distributions, which merely assign labels from a finite set to each data point. As shown for these flows in our prior work, the novel class of quantum state assignment flows can also be characterized as Riemannian gradient flows with respect to a non-local non-convex potential, after proper reparametrization and under mild conditions on the underlying weight function. This weight function generates the parameters of the layers of a neural network, corresponding to and generated by each step of the geometric integration scheme. Numerical results indicates and illustrate the potential of the novel approach for data representation and analysis, including the representation of correlations of data across the graph by entanglement and tensorization.

Variational Monte Carlo Approach to Partial Differential Equations with Neural Networks

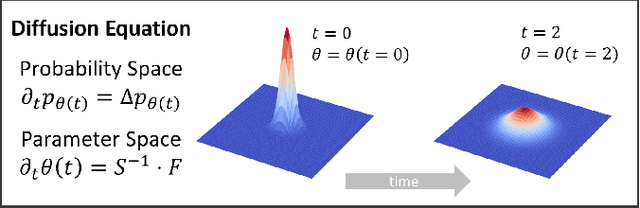
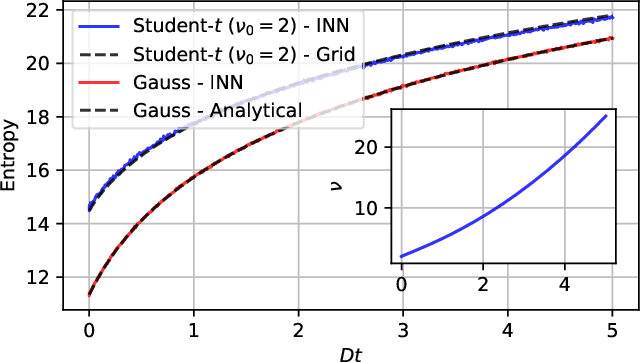
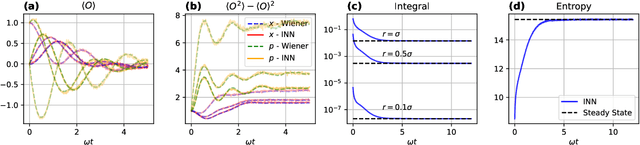
The accurate numerical solution of partial differential equations is a central task in numerical analysis allowing to model a wide range of natural phenomena by employing specialized solvers depending on the scenario of application. Here, we develop a variational approach for solving partial differential equations governing the evolution of high dimensional probability distributions. Our approach naturally works on the unbounded continuous domain and encodes the full probability density function through its variational parameters, which are adapted dynamically during the evolution to optimally reflect the dynamics of the density. For the considered benchmark cases we observe excellent agreement with numerical solutions as well as analytical solutions in regimes inaccessible to traditional computational approaches.

Variational learning of quantum ground states on spiking neuromorphic hardware

We train a neuromorphic hardware chip to approximate the ground states of quantum spin models by variational energy minimization. Compared to variational artificial neural networks using Markov chain Monte Carlo for sample generation, this approach has the advantage that the neuromorphic device generates samples in a fast and inherently parallel fashion. We develop a training algorithm and apply it to the transverse field Ising model, showing good performance at moderate system sizes ($N\leq 10$). A systematic hyperparameter study shows that scalability to larger system sizes mainly depends on sample quality which is limited by parameter drifts on the analog neuromorphic chip. The learning performance shows a threshold behavior as a function of the number of variational parameters of the ansatz, with approximately $50$ hidden neurons being sufficient for representing critical ground states up to $N=10$. The 6+1-bit resolution of the network parameters does not limit the reachable approximation quality in the current setup. Our work provides an important step towards harnessing the capabilities of neuromorphic hardware for tackling the curse of dimensionality in quantum many-body problems.

Spiking neuromorphic chip learns entangled quantum states

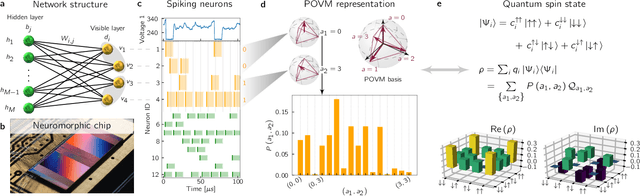
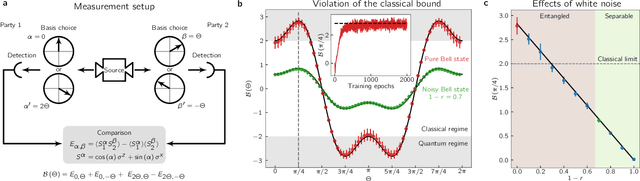
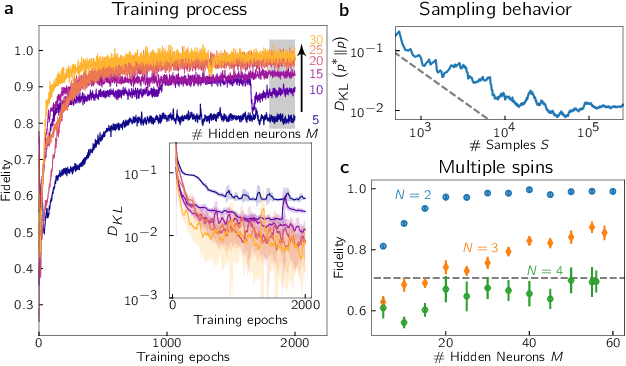
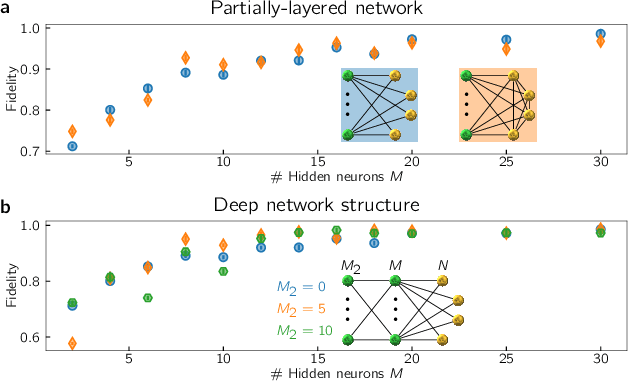
Neuromorphic systems are designed to emulate certain structural and dynamical properties of biological neuronal networks, with the aim of inheriting the brain's functional performance and energy efficiency in artificial-intelligence applications [1,2]. Among the platforms existing today, the spike-based BrainScaleS system stands out by realizing fast analog dynamics which can boost computationally expensive tasks [3]. Here we use the latest BrainScaleS generation [4] for the algorithm-free simulation of quantum systems, thereby opening up an entirely new application space for these devices. This requires an appropriate spike-based representation of quantum states and an associated training method for imprinting a desired target state onto the network. We employ a representation of quantum states using probability distributions [5,6], enabling the use of a Bayesian sampling framework for spiking neurons [7]. For training, we developed a Hebbian learning scheme that explicitly exploits the inherent speed of the substrate, which enables us to realize a variety of network topologies. We encoded maximally entangled states of up to four qubits and observed fidelities that imply genuine $N$-partite entanglement. In particular, the encoding of entangled pure and mixed two-qubit states reaches a quality that allows the observation of Bell correlations, thus demonstrating that non-classical features of quantum systems can be captured by spiking neural dynamics. Our work establishes an intriguing connection between quantum systems and classical spiking networks, and demonstrates the feasibility of simulating quantum systems with neuromorphic hardware.