Dynamic Operating System Scheduling Using Double DQN: A Reinforcement Learning Approach to Task Optimization

In this paper, an operating system scheduling algorithm based on Double DQN (Double Deep Q network) is proposed, and its performance under different task types and system loads is verified by experiments. Compared with the traditional scheduling algorithm, the algorithm based on Double DQN can dynamically adjust the task priority and resource allocation strategy, thus improving the task completion efficiency, system throughput, and response speed. The experimental results show that the Double DQN algorithm has high scheduling performance under light load, medium load and heavy load scenarios, especially when dealing with I/O intensive tasks, and can effectively reduce task completion time and system response time. In addition, the algorithm also shows high optimization ability in resource utilization and can intelligently adjust resource allocation according to the system state, avoiding resource waste and excessive load. Future studies will further explore the application of the algorithm in more complex systems, especially scheduling optimization in cloud computing and large-scale distributed environments, combining factors such as network latency and energy efficiency to improve the overall performance and adaptability of the algorithm.

Unsupervised Detection of Fraudulent Transactions in E-commerce Using Contrastive Learning

With the rapid development of e-commerce, e-commerce platforms are facing an increasing number of fraud threats. Effectively identifying and preventing these fraudulent activities has become a critical research problem. Traditional fraud detection methods typically rely on supervised learning, which requires large amounts of labeled data. However, such data is often difficult to obtain, and the continuous evolution of fraudulent activities further reduces the adaptability and effectiveness of traditional methods. To address this issue, this study proposes an unsupervised e-commerce fraud detection algorithm based on SimCLR. The algorithm leverages the contrastive learning framework to effectively detect fraud by learning the underlying representations of transaction data in an unlabeled setting. Experimental results on the eBay platform dataset show that the proposed algorithm outperforms traditional unsupervised methods such as K-means, Isolation Forest, and Autoencoders in terms of accuracy, precision, recall, and F1 score, demonstrating strong fraud detection capabilities. The results confirm that the SimCLR-based unsupervised fraud detection method has broad application prospects in e-commerce platform security, improving both detection accuracy and robustness. In the future, with the increasing scale and diversity of datasets, the model's performance will continue to improve, and it could be integrated with real-time monitoring systems to provide more efficient security for e-commerce platforms.

Retrieval Backward Attention without Additional Training: Enhance Embeddings of Large Language Models via Repetition

Language models can be viewed as functions that embed text into Euclidean space, where the quality of the embedding vectors directly determines model performance, training such neural networks involves various uncertainties. This paper focuses on improving the performance of pre-trained language models in zero-shot settings through a simple and easily implementable method. We propose a novel backward attention mechanism to enhance contextual information encoding. Evaluated on the Chinese Massive Text Embedding Benchmark (C-MTEB), our approach achieves significant improvements across multiple tasks, providing valuable insights for advancing zero-shot learning capabilities.

Baichuan-M1: Pushing the Medical Capability of Large Language Models

The current generation of large language models (LLMs) is typically designed for broad, general-purpose applications, while domain-specific LLMs, especially in vertical fields like medicine, remain relatively scarce. In particular, the development of highly efficient and practical LLMs for the medical domain is challenging due to the complexity of medical knowledge and the limited availability of high-quality data. To bridge this gap, we introduce Baichuan-M1, a series of large language models specifically optimized for medical applications. Unlike traditional approaches that simply continue pretraining on existing models or apply post-training to a general base model, Baichuan-M1 is trained from scratch with a dedicated focus on enhancing medical capabilities. Our model is trained on 20 trillion tokens and incorporates a range of effective training methods that strike a balance between general capabilities and medical expertise. As a result, Baichuan-M1 not only performs strongly across general domains such as mathematics and coding but also excels in specialized medical fields. We have open-sourced Baichuan-M1-14B, a mini version of our model, which can be accessed through the following links.

Baichuan-Omni-1.5 Technical Report

We introduce Baichuan-Omni-1.5, an omni-modal model that not only has omni-modal understanding capabilities but also provides end-to-end audio generation capabilities. To achieve fluent and high-quality interaction across modalities without compromising the capabilities of any modality, we prioritized optimizing three key aspects. First, we establish a comprehensive data cleaning and synthesis pipeline for multimodal data, obtaining about 500B high-quality data (text, audio, and vision). Second, an audio-tokenizer (Baichuan-Audio-Tokenizer) has been designed to capture both semantic and acoustic information from audio, enabling seamless integration and enhanced compatibility with MLLM. Lastly, we designed a multi-stage training strategy that progressively integrates multimodal alignment and multitask fine-tuning, ensuring effective synergy across all modalities. Baichuan-Omni-1.5 leads contemporary models (including GPT4o-mini and MiniCPM-o 2.6) in terms of comprehensive omni-modal capabilities. Notably, it achieves results comparable to leading models such as Qwen2-VL-72B across various multimodal medical benchmarks.

In-Context Learning Distillation for Efficient Few-Shot Fine-Tuning

We applied few-shot in-context learning on the OPT-1.3B model for the natural language inference task and employed knowledge distillation to internalize the context information, reducing model parameter from 1.3B to 125M and achieving a size reduction from 2.5GB to 0.25GB. Compared to using in-context learning alone on similarly sized models, this context distillation approach achieved a nearly 50% improvement in out-of-domain accuracy, demonstrating superior knowledge transfer capabilities over prompt-based methods. Furthermore, this approach reduced memory consumption by up to 60% while delivering a 20% improvement in out-of-domain accuracy compared to conventional pattern-based fine-tuning.

A Minimal Control Family of Dynamical Syetem for Universal Approximation

The universal approximation property (UAP) of neural networks is a fundamental characteristic of deep learning. It is widely recognized that a composition of linear functions and non-linear functions, such as the rectified linear unit (ReLU) activation function, can approximate continuous functions on compact domains. In this paper, we extend this efficacy to the scenario of dynamical systems with controls. We prove that the control family $\mathcal{F}_1 = \mathcal{F}_0 \cup \{ \text{ReLU}(\cdot)\} $ is enough to generate flow maps that can uniformly approximate diffeomorphisms of $\mathbb{R}^d$ on any compact domain, where $\mathcal{F}_0 = \{x \mapsto Ax+b: A\in \mathbb{R}^{d\times d}, b \in \mathbb{R}^d\}$ is the set of linear maps and the dimension $d\ge2$. Since $\mathcal{F}_1$ contains only one nonlinear function and $\mathcal{F}_0$ does not hold the UAP, we call $\mathcal{F}_1$ a minimal control family for UAP. Based on this, some sufficient conditions, such as the affine invariance, on the control family are established and discussed. Our result reveals an underlying connection between the approximation power of neural networks and control systems.

Minimum Width of Leaky-ReLU Neural Networks for Uniform Universal Approximation

The study of universal approximation properties (UAP) for neural networks (NN) has a long history. When the network width is unlimited, only a single hidden layer is sufficient for UAP. In contrast, when the depth is unlimited, the width for UAP needs to be not less than the critical width $w^*_{\min}=\max(d_x,d_y)$, where $d_x$ and $d_y$ are the dimensions of the input and output, respectively. Recently, \cite{cai2022achieve} shows that a leaky-ReLU NN with this critical width can achieve UAP for $L^p$ functions on a compact domain $K$, \emph{i.e.,} the UAP for $L^p(K,\mathbb{R}^{d_y})$. This paper examines a uniform UAP for the function class $C(K,\mathbb{R}^{d_y})$ and gives the exact minimum width of the leaky-ReLU NN as $w_{\min}=\max(d_x+1,d_y)+1_{d_y=d_x+1}$, which involves the effects of the output dimensions. To obtain this result, we propose a novel lift-flow-discretization approach that shows that the uniform UAP has a deep connection with topological theory.

Vanilla feedforward neural networks as a discretization of dynamic systems

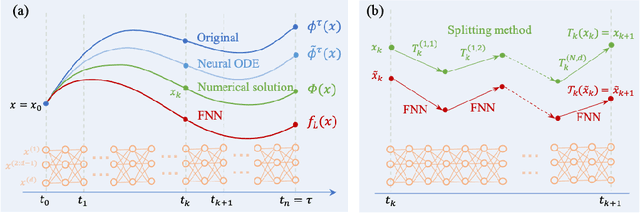
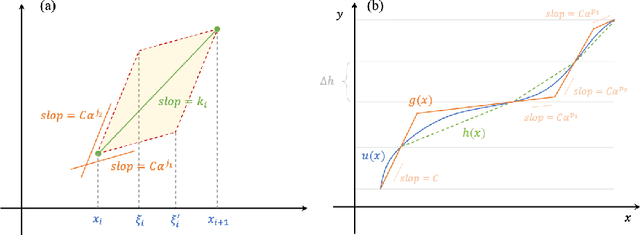
Deep learning has made significant applications in the field of data science and natural science. Some studies have linked deep neural networks to dynamic systems, but the network structure is restricted to the residual network. It is known that residual networks can be regarded as a numerical discretization of dynamic systems. In this paper, we back to the classical network structure and prove that the vanilla feedforward networks could also be a numerical discretization of dynamic systems, where the width of the network is equal to the dimension of the input and output. Our proof is based on the properties of the leaky-ReLU function and the numerical technique of splitting method to solve differential equations. Our results could provide a new perspective for understanding the approximation properties of feedforward neural networks.