Retrieval Backward Attention without Additional Training: Enhance Embeddings of Large Language Models via Repetition

Language models can be viewed as functions that embed text into Euclidean space, where the quality of the embedding vectors directly determines model performance, training such neural networks involves various uncertainties. This paper focuses on improving the performance of pre-trained language models in zero-shot settings through a simple and easily implementable method. We propose a novel backward attention mechanism to enhance contextual information encoding. Evaluated on the Chinese Massive Text Embedding Benchmark (C-MTEB), our approach achieves significant improvements across multiple tasks, providing valuable insights for advancing zero-shot learning capabilities.

Neural Networks Trained by Weight Permutation are Universal Approximators

The universal approximation property is fundamental to the success of neural networks, and has traditionally been achieved by training networks without any constraints on their parameters. However, recent experimental research proposed a novel permutation-based training method, which exhibited a desired classification performance without modifying the exact weight values. In this paper, we provide a theoretical guarantee of this permutation training method by proving its ability to guide a ReLU network to approximate one-dimensional continuous functions. Our numerical results further validate this method's efficiency in regression tasks with various initializations. The notable observations during weight permutation suggest that permutation training can provide an innovative tool for describing network learning behavior.

A Minimal Control Family of Dynamical Syetem for Universal Approximation

The universal approximation property (UAP) of neural networks is a fundamental characteristic of deep learning. It is widely recognized that a composition of linear functions and non-linear functions, such as the rectified linear unit (ReLU) activation function, can approximate continuous functions on compact domains. In this paper, we extend this efficacy to the scenario of dynamical systems with controls. We prove that the control family $\mathcal{F}_1 = \mathcal{F}_0 \cup \{ \text{ReLU}(\cdot)\} $ is enough to generate flow maps that can uniformly approximate diffeomorphisms of $\mathbb{R}^d$ on any compact domain, where $\mathcal{F}_0 = \{x \mapsto Ax+b: A\in \mathbb{R}^{d\times d}, b \in \mathbb{R}^d\}$ is the set of linear maps and the dimension $d\ge2$. Since $\mathcal{F}_1$ contains only one nonlinear function and $\mathcal{F}_0$ does not hold the UAP, we call $\mathcal{F}_1$ a minimal control family for UAP. Based on this, some sufficient conditions, such as the affine invariance, on the control family are established and discussed. Our result reveals an underlying connection between the approximation power of neural networks and control systems.

Minimum Width of Leaky-ReLU Neural Networks for Uniform Universal Approximation

The study of universal approximation properties (UAP) for neural networks (NN) has a long history. When the network width is unlimited, only a single hidden layer is sufficient for UAP. In contrast, when the depth is unlimited, the width for UAP needs to be not less than the critical width $w^*_{\min}=\max(d_x,d_y)$, where $d_x$ and $d_y$ are the dimensions of the input and output, respectively. Recently, \cite{cai2022achieve} shows that a leaky-ReLU NN with this critical width can achieve UAP for $L^p$ functions on a compact domain $K$, \emph{i.e.,} the UAP for $L^p(K,\mathbb{R}^{d_y})$. This paper examines a uniform UAP for the function class $C(K,\mathbb{R}^{d_y})$ and gives the exact minimum width of the leaky-ReLU NN as $w_{\min}=\max(d_x+1,d_y)+1_{d_y=d_x+1}$, which involves the effects of the output dimensions. To obtain this result, we propose a novel lift-flow-discretization approach that shows that the uniform UAP has a deep connection with topological theory.

Vocabulary for Universal Approximation: A Linguistic Perspective of Mapping Compositions

In recent years, deep learning-based sequence modelings, such as language models, have received much attention and success, which pushes researchers to explore the possibility of transforming non-sequential problems into a sequential form. Following this thought, deep neural networks can be represented as composite functions of a sequence of mappings, linear or nonlinear, where each composition can be viewed as a \emph{word}. However, the weights of linear mappings are undetermined and hence require an infinite number of words. In this article, we investigate the finite case and constructively prove the existence of a finite \emph{vocabulary} $V=\{\phi_i: \mathbb{R}^d \to \mathbb{R}^d | i=1,...,n\}$ with $n=O(d^2)$ for the universal approximation. That is, for any continuous mapping $f: \mathbb{R}^d \to \mathbb{R}^d$, compact domain $\Omega$ and $\varepsilon>0$, there is a sequence of mappings $\phi_{i_1}, ..., \phi_{i_m} \in V, m \in \mathbb{Z}_+$, such that the composition $\phi_{i_m} \circ ... \circ \phi_{i_1} $ approximates $f$ on $\Omega$ with an error less than $\varepsilon$. Our results provide a linguistic perspective of composite mappings and suggest a cross-disciplinary study between linguistics and approximation theory.

Achieve the Minimum Width of Neural Networks for Universal Approximation

The universal approximation property (UAP) of neural networks is fundamental for deep learning, and it is well known that wide neural networks are universal approximators of continuous functions within both the $L^p$ norm and the continuous/uniform norm. However, the exact minimum width, $w_{\min}$, for the UAP has not been studied thoroughly. Recently, using a decoder-memorizer-encoder scheme, \citet{Park2021Minimum} found that $w_{\min} = \max(d_x+1,d_y)$ for both the $L^p$-UAP of ReLU networks and the $C$-UAP of ReLU+STEP networks, where $d_x,d_y$ are the input and output dimensions, respectively. In this paper, we consider neural networks with an arbitrary set of activation functions. We prove that both $C$-UAP and $L^p$-UAP for functions on compact domains share a universal lower bound of the minimal width; that is, $w^*_{\min} = \max(d_x,d_y)$. In particular, the critical width, $w^*_{\min}$, for $L^p$-UAP can be achieved by leaky-ReLU networks, provided that the input or output dimension is larger than one. Our construction is based on the approximation power of neural ordinary differential equations and the ability to approximate flow maps by neural networks. The nonmonotone or discontinuous activation functions case and the one-dimensional case are also discussed.

Vanilla feedforward neural networks as a discretization of dynamic systems

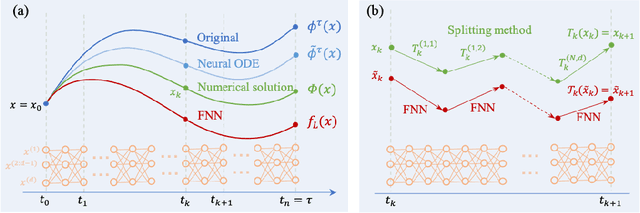
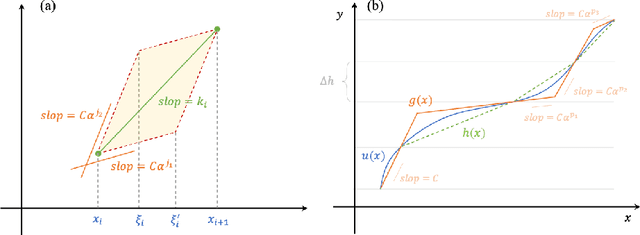
Deep learning has made significant applications in the field of data science and natural science. Some studies have linked deep neural networks to dynamic systems, but the network structure is restricted to the residual network. It is known that residual networks can be regarded as a numerical discretization of dynamic systems. In this paper, we back to the classical network structure and prove that the vanilla feedforward networks could also be a numerical discretization of dynamic systems, where the width of the network is equal to the dimension of the input and output. Our proof is based on the properties of the leaky-ReLU function and the numerical technique of splitting method to solve differential equations. Our results could provide a new perspective for understanding the approximation properties of feedforward neural networks.

Optimization in Machine Learning: A Distribution Space Approach

We present the viewpoint that optimization problems encountered in machine learning can often be interpreted as minimizing a convex functional over a function space, but with a non-convex constraint set introduced by model parameterization. This observation allows us to repose such problems via a suitable relaxation as convex optimization problems in the space of distributions over the training parameters. We derive some simple relationships between the distribution-space problem and the original problem, e.g. a distribution-space solution is at least as good as a solution in the original space. Moreover, we develop a numerical algorithm based on mixture distributions to perform approximate optimization directly in distribution space. Consistency of this approximation is established and the numerical efficacy of the proposed algorithm is illustrated on simple examples. In both theory and practice, this formulation provides an alternative approach to large-scale optimization in machine learning.

On the Convergence and Robustness of Batch Normalization

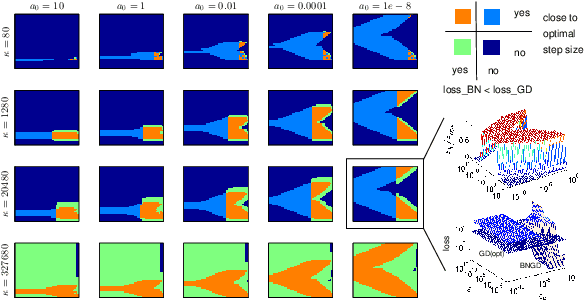
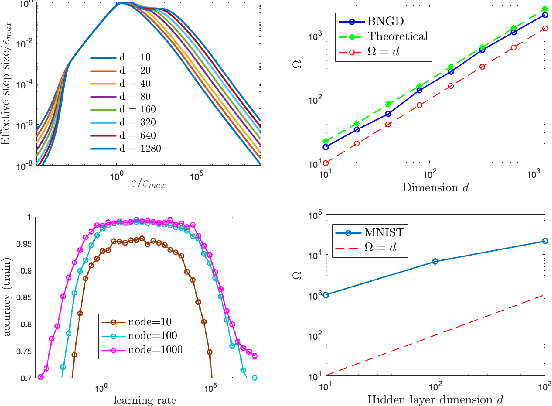
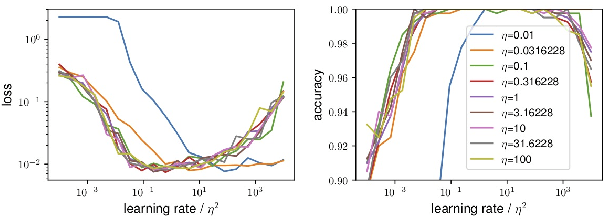
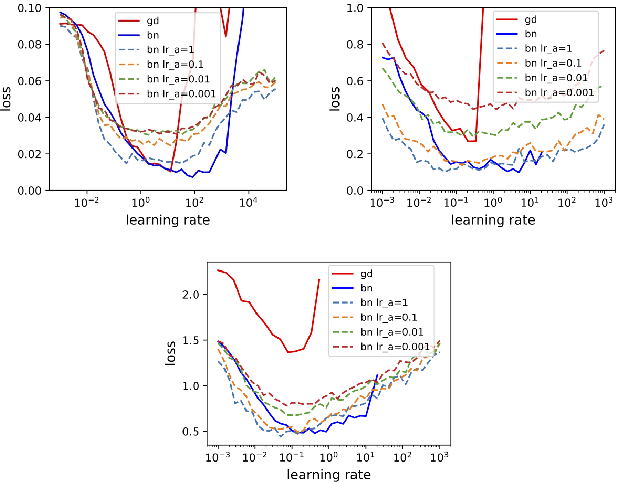
Despite its empirical success, the theoretical underpinnings of the stability, convergence and acceleration properties of batch normalization (BN) remain elusive. In this paper, we attack this problem from a modeling approach, where we perform a thorough theoretical analysis on BN applied to a simplified model: ordinary least squares (OLS). We discover that gradient descent on OLS with BN has interesting properties, including a scaling law, convergence for arbitrary learning rates for the weights, asymptotic acceleration effects, as well as insensitivity to the choice of learning rates. We then demonstrate numerically that these findings are not specific to the OLS problem and hold qualitatively for more complex supervised learning problems. This points to a new direction towards uncovering the mathematical principles that underlies batch normalization.