IELDG: Suppressing Domain-Specific Noise with Inverse Evolution Layers for Domain Generalized Semantic Segmentation

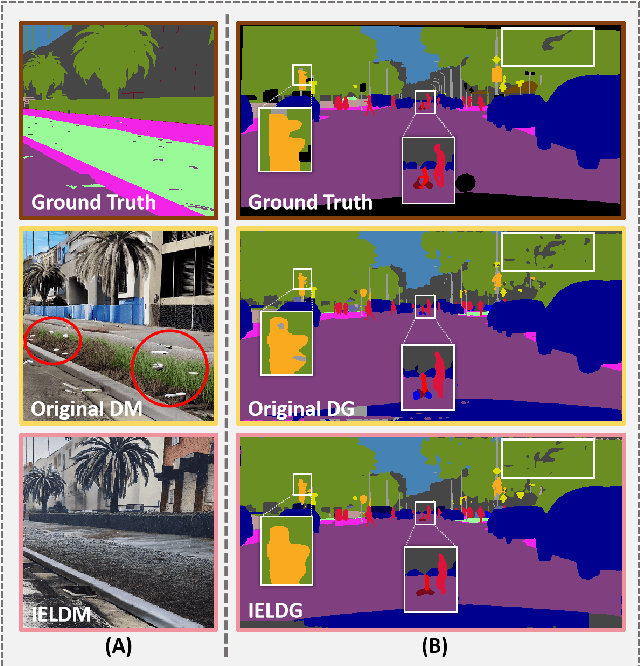
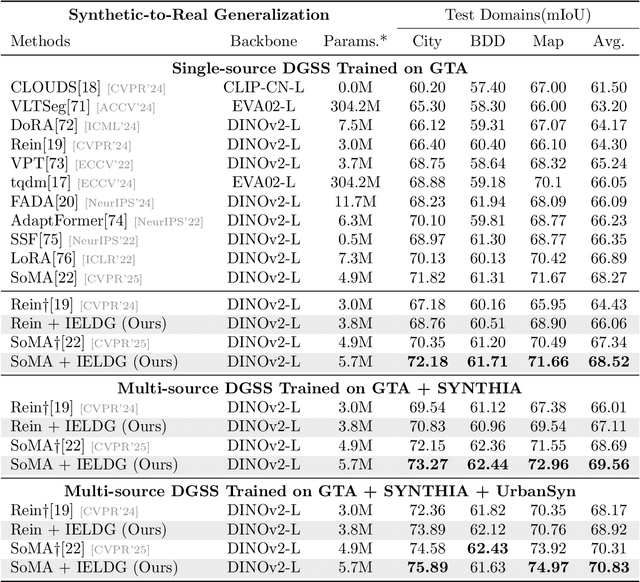
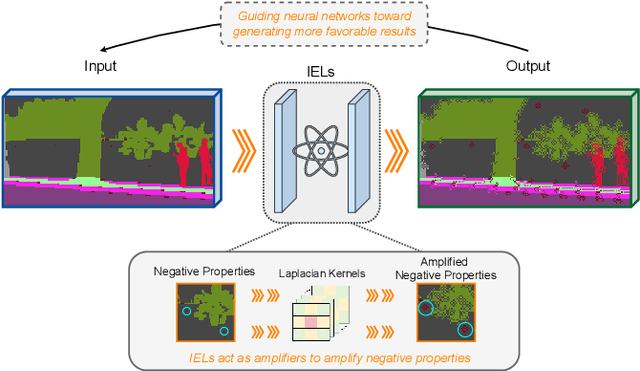
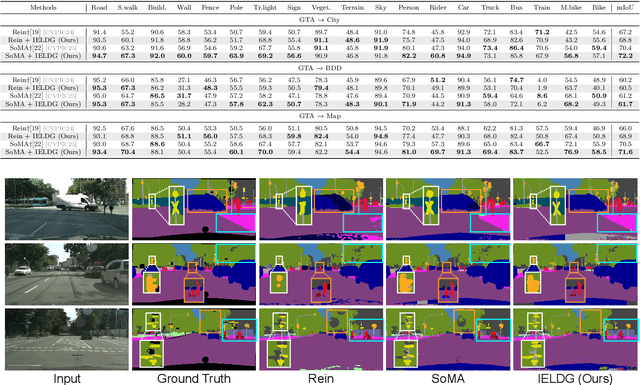
Domain Generalized Semantic Segmentation (DGSS) focuses on training a model using labeled data from a source domain, with the goal of achieving robust generalization to unseen target domains during inference. A common approach to improve generalization is to augment the source domain with synthetic data generated by diffusion models (DMs). However, the generated images often contain structural or semantic defects due to training imperfections. Training segmentation models with such flawed data can lead to performance degradation and error accumulation. To address this issue, we propose to integrate inverse evolution layers (IELs) into the generative process. IELs are designed to highlight spatial discontinuities and semantic inconsistencies using Laplacian-based priors, enabling more effective filtering of undesirable generative patterns. Based on this mechanism, we introduce IELDM, an enhanced diffusion-based data augmentation framework that can produce higher-quality images. Furthermore, we observe that the defect-suppression capability of IELs can also benefit the segmentation network by suppressing artifact propagation. Based on this insight, we embed IELs into the decoder of the DGSS model and propose IELFormer to strengthen generalization capability in cross-domain scenarios. To further strengthen the model's semantic consistency across scales, IELFormer incorporates a multi-scale frequency fusion (MFF) module, which performs frequency-domain analysis to achieve structured integration of multi-resolution features, thereby improving cross-scale coherence. Extensive experiments on benchmark datasets demonstrate that our approach achieves superior generalization performance compared to existing methods.

Sidecar: A Structure-Preserving Framework for Solving Partial Differential Equations with Neural Networks

Solving partial differential equations (PDEs) with neural networks (NNs) has shown great potential in various scientific and engineering fields. However, most existing NN solvers mainly focus on satisfying the given PDEs, without explicitly considering intrinsic physical properties such as mass conservation or energy dissipation. This limitation can result in unstable or nonphysical solutions, particularly in long-term simulations. To address this issue, we propose Sidecar, a novel framework that enhances the accuracy and physical consistency of existing NN solvers by incorporating structure-preserving knowledge. Inspired by the Time-Dependent Spectral Renormalization (TDSR) approach, our Sidecar framework introduces a small copilot network, which is trained to guide the existing NN solver in preserving physical structure. This framework is designed to be highly flexible, enabling the incorporation of structure-preserving principles from diverse PDEs into a wide range of NN solvers. Our experimental results on benchmark PDEs demonstrate the improvement of the existing neural network solvers in terms of accuracy and consistency with structure-preserving properties.

Neural Networks Trained by Weight Permutation are Universal Approximators

The universal approximation property is fundamental to the success of neural networks, and has traditionally been achieved by training networks without any constraints on their parameters. However, recent experimental research proposed a novel permutation-based training method, which exhibited a desired classification performance without modifying the exact weight values. In this paper, we provide a theoretical guarantee of this permutation training method by proving its ability to guide a ReLU network to approximate one-dimensional continuous functions. Our numerical results further validate this method's efficiency in regression tasks with various initializations. The notable observations during weight permutation suggest that permutation training can provide an innovative tool for describing network learning behavior.

Inverse Evolution Layers: Physics-informed Regularizers for Deep Neural Networks

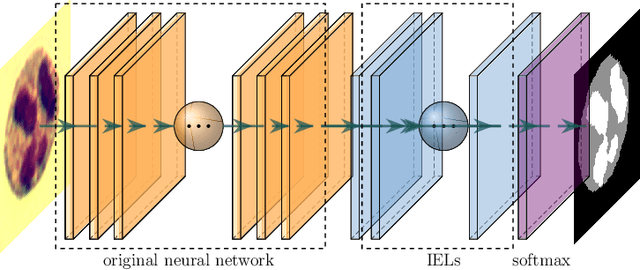
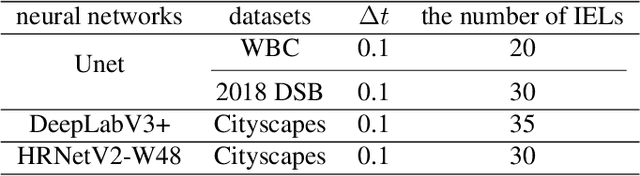
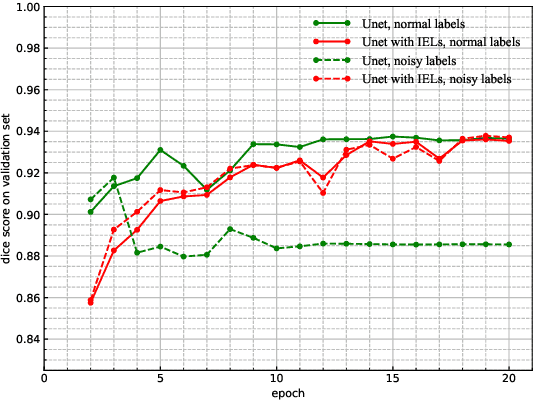
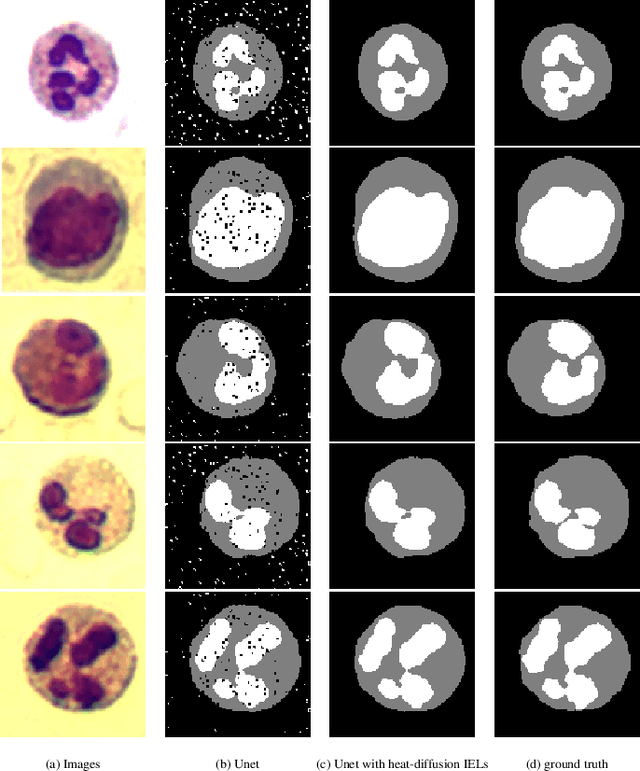
This paper proposes a novel approach to integrating partial differential equation (PDE)-based evolution models into neural networks through a new type of regularization. Specifically, we propose inverse evolution layers (IELs) based on evolution equations. These layers can achieve specific regularization objectives and endow neural networks' outputs with corresponding properties of the evolution models. Moreover, IELs are straightforward to construct and implement, and can be easily designed for various physical evolutions and neural networks. Additionally, the design process for these layers can provide neural networks with intuitive and mathematical interpretability, thus enhancing the transparency and explainability of the approach. To demonstrate the effectiveness, efficiency, and simplicity of our approach, we present an example of endowing semantic segmentation models with the smoothness property based on the heat diffusion model. To achieve this goal, we design heat-diffusion IELs and apply them to address the challenge of semantic segmentation with noisy labels. The experimental results demonstrate that the heat-diffusion IELs can effectively mitigate the overfitting problem caused by noisy labels.

An Active Contour Model with Local Variance Force Term and Its Efficient Minimization Solver for Multi-phase Image Segmentation

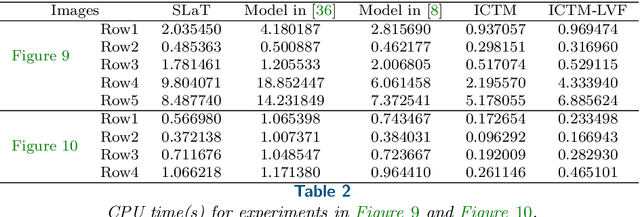
In this paper, we propose an active contour model with a local variance force (LVF) term that can be applied to multi-phase image segmentation problems. With the LVF, the proposed model is very effective in the segmentation of images with noise. To solve this model efficiently, we represent the regularization term by characteristic functions and then design a minimization algorithm based on a modification of the iterative convolution-thresholding method (ICTM), namely ICTM-LVF. This minimization algorithm enjoys the energy-decaying property under some conditions and has highly efficient performance in the segmentation. To overcome the initialization issue of active contour models, we generalize the inhomogeneous graph Laplacian initialization method (IGLIM) to the multi-phase case and then apply it to give the initial contour of the ICTM-LVF solver. Numerical experiments are conducted on synthetic images and real images to demonstrate the capability of our initialization method, and the effectiveness of the local variance force for noise robustness in the multi-phase image segmentation.