GeoSplat: A Deep Dive into Geometry-Constrained Gaussian Splatting

A few recent works explored incorporating geometric priors to regularize the optimization of Gaussian splatting, further improving its performance. However, those early studies mainly focused on the use of low-order geometric priors (e.g., normal vector), and they are also unreliably estimated by noise-sensitive methods, like local principal component analysis. To address their limitations, we first present GeoSplat, a general geometry-constrained optimization framework that exploits both first-order and second-order geometric quantities to improve the entire training pipeline of Gaussian splatting, including Gaussian initialization, gradient update, and densification. As an example, we initialize the scales of 3D Gaussian primitives in terms of principal curvatures, leading to a better coverage of the object surface than random initialization. Secondly, based on certain geometric structures (e.g., local manifold), we introduce efficient and noise-robust estimation methods that provide dynamic geometric priors for our framework. We conduct extensive experiments on multiple datasets for novel view synthesis, showing that our framework: GeoSplat, significantly improves the performance of Gaussian splatting and outperforms previous baselines.

IELDG: Suppressing Domain-Specific Noise with Inverse Evolution Layers for Domain Generalized Semantic Segmentation

Domain Generalized Semantic Segmentation (DGSS) focuses on training a model using labeled data from a source domain, with the goal of achieving robust generalization to unseen target domains during inference. A common approach to improve generalization is to augment the source domain with synthetic data generated by diffusion models (DMs). However, the generated images often contain structural or semantic defects due to training imperfections. Training segmentation models with such flawed data can lead to performance degradation and error accumulation. To address this issue, we propose to integrate inverse evolution layers (IELs) into the generative process. IELs are designed to highlight spatial discontinuities and semantic inconsistencies using Laplacian-based priors, enabling more effective filtering of undesirable generative patterns. Based on this mechanism, we introduce IELDM, an enhanced diffusion-based data augmentation framework that can produce higher-quality images. Furthermore, we observe that the defect-suppression capability of IELs can also benefit the segmentation network by suppressing artifact propagation. Based on this insight, we embed IELs into the decoder of the DGSS model and propose IELFormer to strengthen generalization capability in cross-domain scenarios. To further strengthen the model's semantic consistency across scales, IELFormer incorporates a multi-scale frequency fusion (MFF) module, which performs frequency-domain analysis to achieve structured integration of multi-resolution features, thereby improving cross-scale coherence. Extensive experiments on benchmark datasets demonstrate that our approach achieves superior generalization performance compared to existing methods.

Conservation-preserved Fourier Neural Operator through Adaptive Correction

Fourier Neural Operators (FNOs) have recently emerged as a promising and efficient approach for learning the numerical solutions to partial differential equations (PDEs) from data. However, standard FNO often fails to preserve key conservation laws, such as mass conservation, momentum conservation, norm conservation, etc., which are crucial for accurately modeling physical systems. Existing methods for incorporating these conservation laws into Fourier neural operators are achieved by designing related loss function or incorporating post-processing method at the training time. None of them can both exactly and adaptively correct the outputs to satisfy conservation laws, and our experiments show that these methods can lead to inferior performance while preserving conservation laws. In this work, we propose a novel adaptive correction approach to ensure the conservation of fundamental quantities. Our method introduces a learnable matrix to adaptively adjust the solution to satisfy the conservation law during training. It ensures that the outputs exactly satisfy the goal conservation law and allow for more flexibility and adaptivity for the model to correct the outputs. We theoretically show that applying our adaptive correction to an unconstrained FNO yields a solution with data loss no worse than that of the best conservation-satisfying FNO. We compare our approach with existing methods on a range of representative PDEs. Experiment results show that our method consistently outperform other methods.

Brain Foundation Models with Hypergraph Dynamic Adapter for Brain Disease Analysis

Brain diseases, such as Alzheimer's disease and brain tumors, present profound challenges due to their complexity and societal impact. Recent advancements in brain foundation models have shown significant promise in addressing a range of brain-related tasks. However, current brain foundation models are limited by task and data homogeneity, restricted generalization beyond segmentation or classification, and inefficient adaptation to diverse clinical tasks. In this work, we propose SAM-Brain3D, a brain-specific foundation model trained on over 66,000 brain image-label pairs across 14 MRI sub-modalities, and Hypergraph Dynamic Adapter (HyDA), a lightweight adapter for efficient and effective downstream adaptation. SAM-Brain3D captures detailed brain-specific anatomical and modality priors for segmenting diverse brain targets and broader downstream tasks. HyDA leverages hypergraphs to fuse complementary multi-modal data and dynamically generate patient-specific convolutional kernels for multi-scale feature fusion and personalized patient-wise adaptation. Together, our framework excels across a broad spectrum of brain disease segmentation and classification tasks. Extensive experiments demonstrate that our method consistently outperforms existing state-of-the-art approaches, offering a new paradigm for brain disease analysis through multi-modal, multi-scale, and dynamic foundation modeling.

Inverse Evolution Data Augmentation for Neural PDE Solvers

Neural networks have emerged as promising tools for solving partial differential equations (PDEs), particularly through the application of neural operators. Training neural operators typically requires a large amount of training data to ensure accuracy and generalization. In this paper, we propose a novel data augmentation method specifically designed for training neural operators on evolution equations. Our approach utilizes insights from inverse processes of these equations to efficiently generate data from random initialization that are combined with original data. To further enhance the accuracy of the augmented data, we introduce high-order inverse evolution schemes. These schemes consist of only a few explicit computation steps, yet the resulting data pairs can be proven to satisfy the corresponding implicit numerical schemes. In contrast to traditional PDE solvers that require small time steps or implicit schemes to guarantee accuracy, our data augmentation method employs explicit schemes with relatively large time steps, thereby significantly reducing computational costs. Accuracy and efficacy experiments confirm the effectiveness of our approach. Additionally, we validate our approach through experiments with the Fourier Neural Operator and UNet on three common evolution equations that are Burgers' equation, the Allen-Cahn equation and the Navier-Stokes equation. The results demonstrate a significant improvement in the performance and robustness of the Fourier Neural Operator when coupled with our inverse evolution data augmentation method.

Inverse Evolution Layers: Physics-informed Regularizers for Deep Neural Networks

This paper proposes a novel approach to integrating partial differential equation (PDE)-based evolution models into neural networks through a new type of regularization. Specifically, we propose inverse evolution layers (IELs) based on evolution equations. These layers can achieve specific regularization objectives and endow neural networks' outputs with corresponding properties of the evolution models. Moreover, IELs are straightforward to construct and implement, and can be easily designed for various physical evolutions and neural networks. Additionally, the design process for these layers can provide neural networks with intuitive and mathematical interpretability, thus enhancing the transparency and explainability of the approach. To demonstrate the effectiveness, efficiency, and simplicity of our approach, we present an example of endowing semantic segmentation models with the smoothness property based on the heat diffusion model. To achieve this goal, we design heat-diffusion IELs and apply them to address the challenge of semantic segmentation with noisy labels. The experimental results demonstrate that the heat-diffusion IELs can effectively mitigate the overfitting problem caused by noisy labels.

An Active Contour Model with Local Variance Force Term and Its Efficient Minimization Solver for Multi-phase Image Segmentation

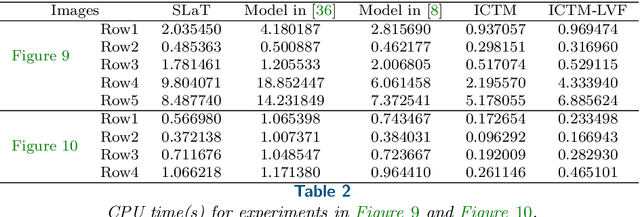
In this paper, we propose an active contour model with a local variance force (LVF) term that can be applied to multi-phase image segmentation problems. With the LVF, the proposed model is very effective in the segmentation of images with noise. To solve this model efficiently, we represent the regularization term by characteristic functions and then design a minimization algorithm based on a modification of the iterative convolution-thresholding method (ICTM), namely ICTM-LVF. This minimization algorithm enjoys the energy-decaying property under some conditions and has highly efficient performance in the segmentation. To overcome the initialization issue of active contour models, we generalize the inhomogeneous graph Laplacian initialization method (IGLIM) to the multi-phase case and then apply it to give the initial contour of the ICTM-LVF solver. Numerical experiments are conducted on synthetic images and real images to demonstrate the capability of our initialization method, and the effectiveness of the local variance force for noise robustness in the multi-phase image segmentation.