Robust State Estimation for Legged Robots with Dual Beta Kalman Filter

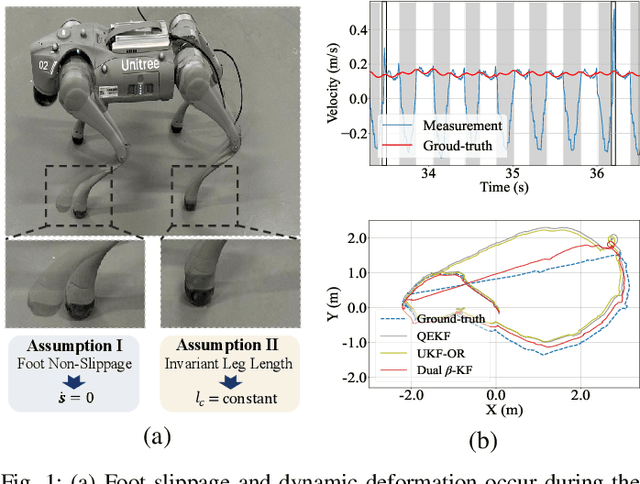
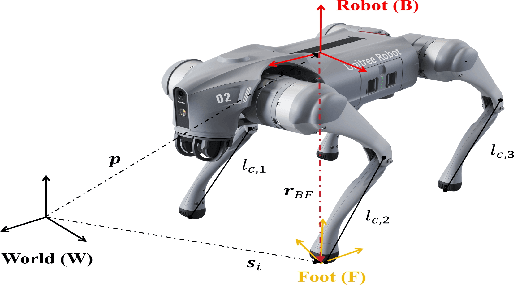
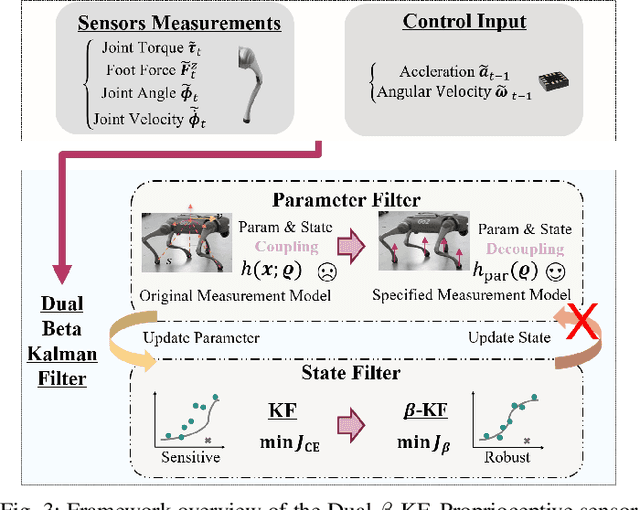
Existing state estimation algorithms for legged robots that rely on proprioceptive sensors often overlook foot slippage and leg deformation in the physical world, leading to large estimation errors. To address this limitation, we propose a comprehensive measurement model that accounts for both foot slippage and variable leg length by analyzing the relative motion between foot contact points and the robot's body center. We show that leg length is an observable quantity, meaning that its value can be explicitly inferred by designing an auxiliary filter. To this end, we introduce a dual estimation framework that iteratively employs a parameter filter to estimate the leg length parameters and a state filter to estimate the robot's state. To prevent error accumulation in this iterative framework, we construct a partial measurement model for the parameter filter using the leg static equation. This approach ensures that leg length estimation relies solely on joint torques and foot contact forces, avoiding the influence of state estimation errors on the parameter estimation. Unlike leg length which can be directly estimated, foot slippage cannot be measured directly with the current sensor configuration. However, since foot slippage occurs at a low frequency, it can be treated as outliers in the measurement data. To mitigate the impact of these outliers, we propose the beta Kalman filter (beta KF), which redefines the estimation loss in canonical Kalman filtering using beta divergence. This divergence can assign low weights to outliers in an adaptive manner, thereby enhancing the robustness of the estimation algorithm. These techniques together form the dual beta-Kalman filter (Dual beta KF), a novel algorithm for robust state estimation in legged robots. Experimental results on the Unitree GO2 robot demonstrate that the Dual beta KF significantly outperforms state-of-the-art methods.

Collecting Larg-Scale Robotic Datasets on a High-Speed Mobile Platform

Mobile robotics datasets are essential for research on robotics, for example for research on Simultaneous Localization and Mapping (SLAM). Therefore the ShanghaiTech Mapping Robot was constructed, that features a multitude high-performance sensors and a 16-node cluster to collect all this data. That robot is based on a Clearpath Husky mobile base with a maximum speed of 1 meter per second. This is fine for indoor datasets, but to collect large-scale outdoor datasets a faster platform is needed. This system paper introduces our high-speed mobile platform for data collection. The mapping robot is secured on the rear-steered flatbed car with maximum field of view. Additionally two encoders collect odometry data from two of the car wheels and an external sensor plate houses a downlooking RGB and event camera. With this setup a dataset of more than 10km in the underground parking garage and the outside of our campus was collected and is published with this paper.

Convolutional Unscented Kalman Filter for Multi-Object Tracking with Outliers

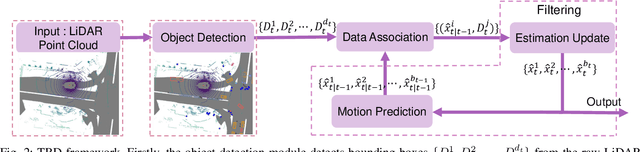
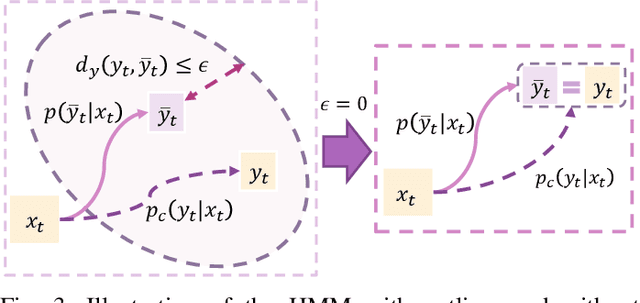
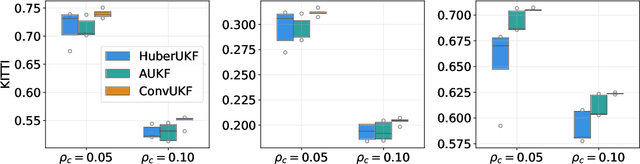
Multi-object tracking (MOT) is an essential technique for navigation in autonomous driving. In tracking-by-detection systems, biases, false positives, and misses, which are referred to as outliers, are inevitable due to complex traffic scenarios. Recent tracking methods are based on filtering algorithms that overlook these outliers, leading to reduced tracking accuracy or even loss of the objects trajectory. To handle this challenge, we adopt a probabilistic perspective, regarding the generation of outliers as misspecification between the actual distribution of measurement data and the nominal measurement model used for filtering. We further demonstrate that, by designing a convolutional operation, we can mitigate this misspecification. Incorporating this operation into the widely used unscented Kalman filter (UKF) in commonly adopted tracking algorithms, we derive a variant of the UKF that is robust to outliers, called the convolutional UKF (ConvUKF). We show that ConvUKF maintains the Gaussian conjugate property, thus allowing for real-time tracking. We also prove that ConvUKF has a bounded tracking error in the presence of outliers, which implies robust stability. The experimental results on the KITTI and nuScenes datasets show improved accuracy compared to representative baseline algorithms for MOT tasks.

Convolutional Bayesian Filtering

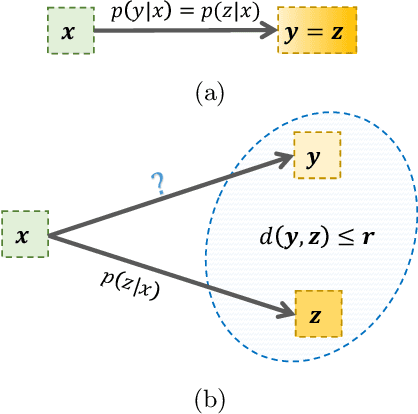
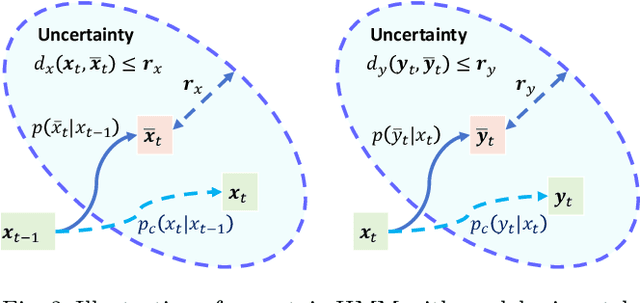
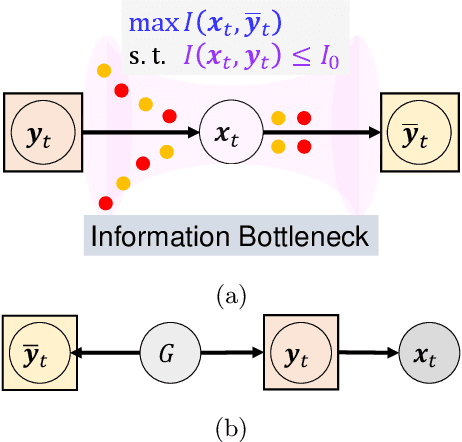
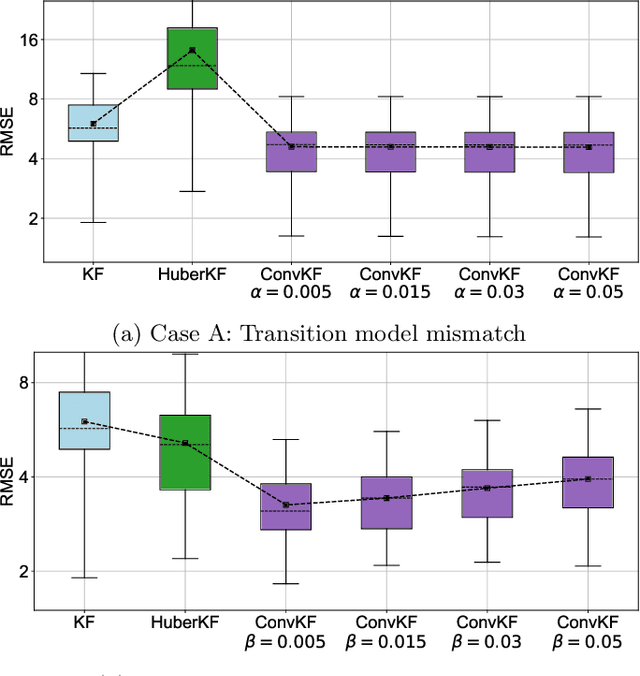
Bayesian filtering serves as the mainstream framework of state estimation in dynamic systems. Its standard version utilizes total probability rule and Bayes' law alternatively, where how to define and compute conditional probability is critical to state distribution inference. Previously, the conditional probability is assumed to be exactly known, which represents a measure of the occurrence probability of one event, given the second event. In this paper, we find that by adding an additional event that stipulates an inequality condition, we can transform the conditional probability into a special integration that is analogous to convolution. Based on this transformation, we show that both transition probability and output probability can be generalized to convolutional forms, resulting in a more general filtering framework that we call convolutional Bayesian filtering. This new framework encompasses standard Bayesian filtering as a special case when the distance metric of the inequality condition is selected as Dirac delta function. It also allows for a more nuanced consideration of model mismatch by choosing different types of inequality conditions. For instance, when the distance metric is defined in a distributional sense, the transition probability and output probability can be approximated by simply rescaling them into fractional powers. Under this framework, a robust version of Kalman filter can be constructed by only altering the noise covariance matrix, while maintaining the conjugate nature of Gaussian distributions. Finally, we exemplify the effectiveness of our approach by reshaping classic filtering algorithms into convolutional versions, including Kalman filter, extended Kalman filter, unscented Kalman filter and particle filter.

Impact of Computation in Integral Reinforcement Learning for Continuous-Time Control

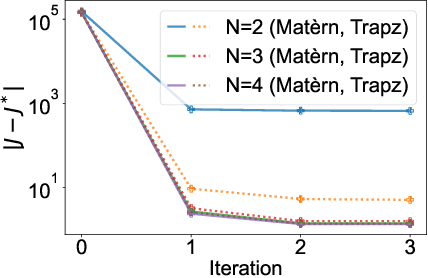
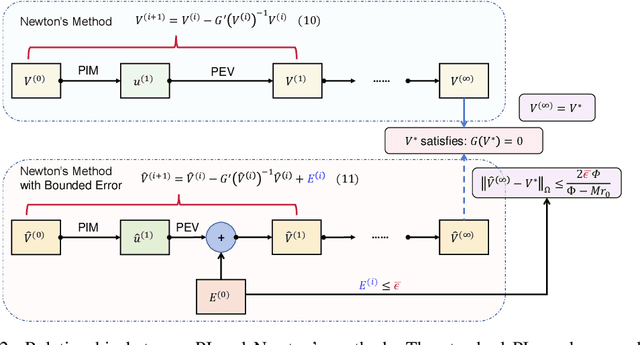
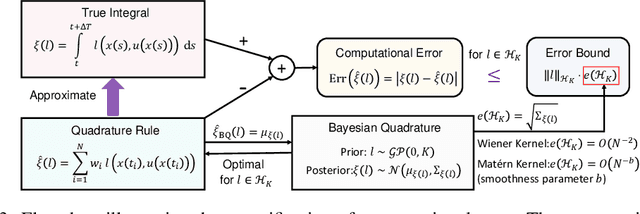
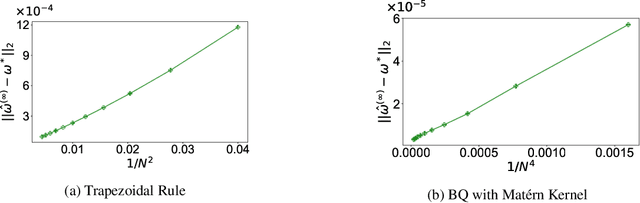
Integral reinforcement learning (IntRL) demands the precise computation of the utility function's integral at its policy evaluation (PEV) stage. This is achieved through quadrature rules, which are weighted sums of utility functions evaluated from state samples obtained in discrete time. Our research reveals a critical yet underexplored phenomenon: the choice of the computational method -- in this case, the quadrature rule -- can significantly impact control performance. This impact is traced back to the fact that computational errors introduced in the PEV stage can affect the policy iteration's convergence behavior, which in turn affects the learned controller. To elucidate how computation impacts control, we draw a parallel between IntRL's policy iteration and Newton's method applied to the Hamilton-Jacobi-Bellman equation. In this light, computational error in PEV manifests as an extra error term in each iteration of Newton's method, with its upper bound proportional to the computational error. Further, we demonstrate that when the utility function resides in a reproducing kernel Hilbert space (RKHS), the optimal quadrature is achievable by employing Bayesian quadrature with the RKHS-inducing kernel function. We prove that the local convergence rates for IntRL using the trapezoidal rule and Bayesian quadrature with a Mat\'ern kernel to be $O(N^{-2})$ and $O(N^{-b})$, where $N$ is the number of evenly-spaced samples and $b$ is the Mat\'ern kernel's smoothness parameter. These theoretical findings are finally validated by two canonical control tasks.

3D-Printed Hydraulic Fluidic Logic Circuitry for Soft Robots

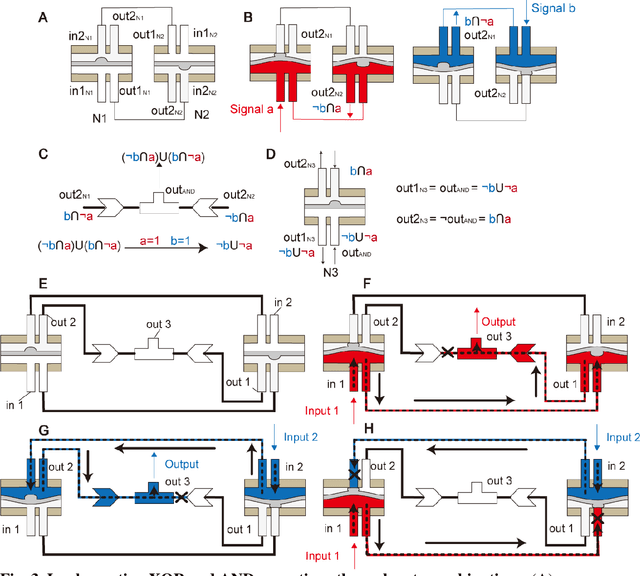
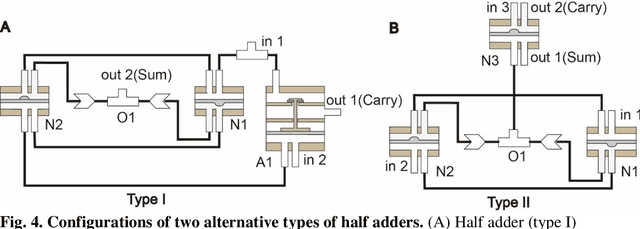
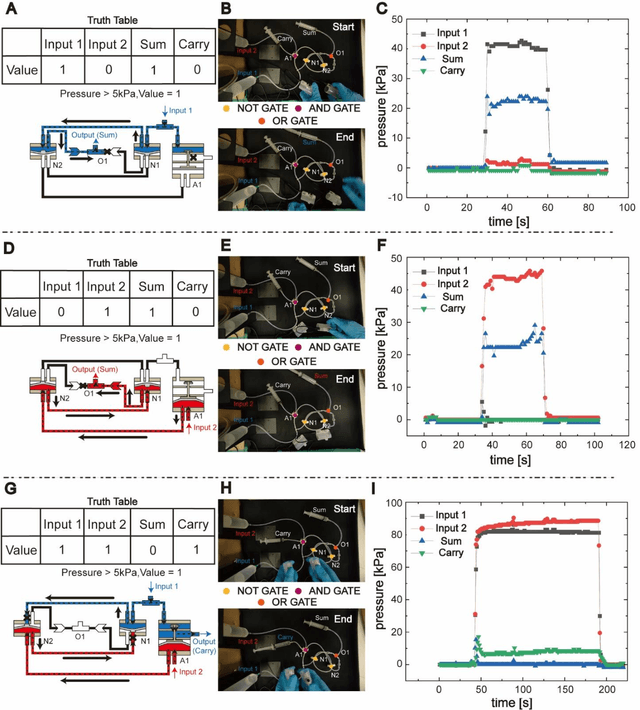
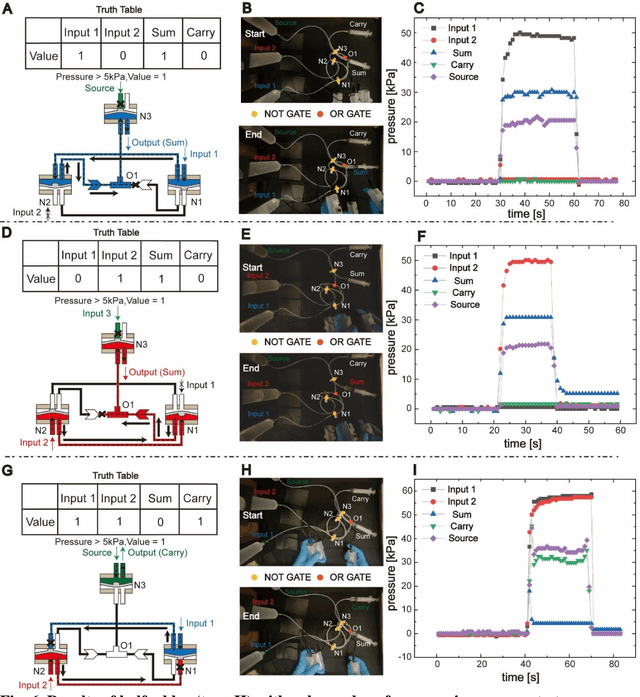
Fluidic logic circuitry analogous to its electric counterpart could potentially provide soft robots with machine intelligence due to its supreme adaptability, dexterity, and seamless compatibility using state-of-the-art additive manufacturing processes. However, conventional microfluidic channel based circuitry suffers from limited driving force, while macroscopic pneumatic logic lacks timely responsivity and desirable accuracy. Producing heavy duty, highly responsive and integrated fluidic soft robotic circuitry for control and actuation purposes for biomedical applications has yet to be accomplished in a hydraulic manner. Here, we present a 3D printed hydraulic fluidic half-adder system, composing of three basic hydraulic fluidic logic building blocks: AND, OR, and NOT gates. Furthermore, a hydraulic soft robotic half-adder system is implemented using an XOR operation and modified dual NOT gate system based on an electrical oscillator structure. This half-adder system possesses binary arithmetic capability as a key component of arithmetic logic unit in modern computers. With slight modifications, it can realize the control over three different directions of deformation of a three degree-of-freedom soft actuation mechanism solely by changing the states of the two fluidic inputs. This hydraulic fluidic system utilizing a small number of inputs to control multiple distinct outputs, can alter the internal state of the circuit solely based on external inputs, holding significant promises for the development of microfluidics, fluidic logic, and intricate internal systems of untethered soft robots with machine intelligence.

On the Optimization Landscape of Dynamic Output Feedback: A Case Study for Linear Quadratic Regulator

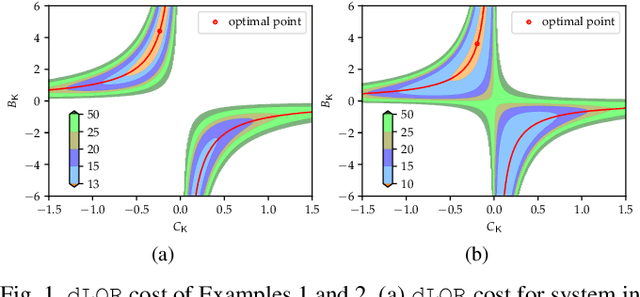
The convergence of policy gradient algorithms in reinforcement learning hinges on the optimization landscape of the underlying optimal control problem. Theoretical insights into these algorithms can often be acquired from analyzing those of linear quadratic control. However, most of the existing literature only considers the optimization landscape for static full-state or output feedback policies (controllers). We investigate the more challenging case of dynamic output-feedback policies for linear quadratic regulation (abbreviated as dLQR), which is prevalent in practice but has a rather complicated optimization landscape. We first show how the dLQR cost varies with the coordinate transformation of the dynamic controller and then derive the optimal transformation for a given observable stabilizing controller. At the core of our results is the uniqueness of the stationary point of dLQR when it is observable, which is in a concise form of an observer-based controller with the optimal similarity transformation. These results shed light on designing efficient algorithms for general decision-making problems with partially observed information.

Approximate Optimal Filter for Linear Gaussian Time-invariant Systems

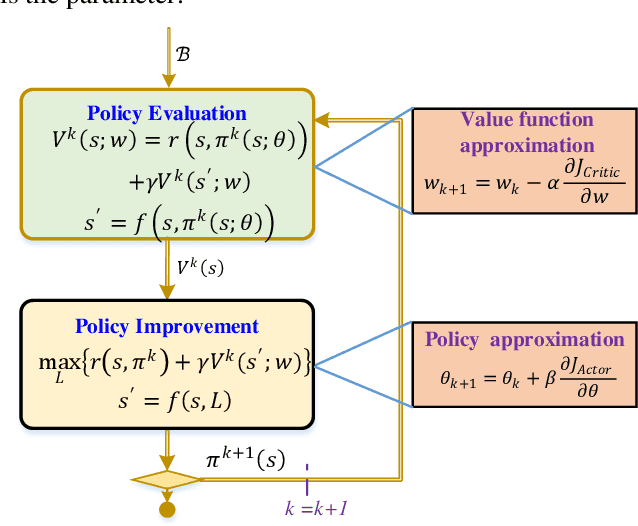
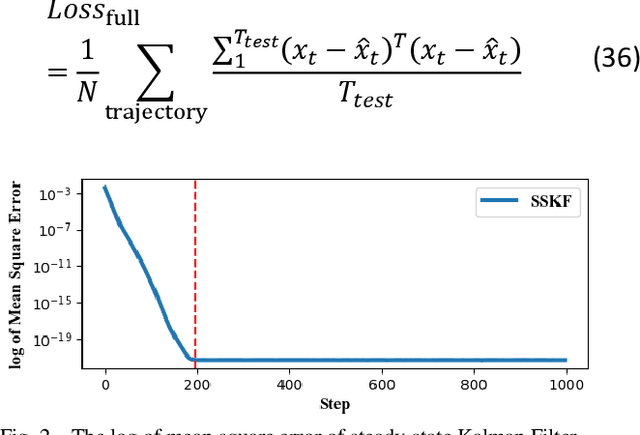
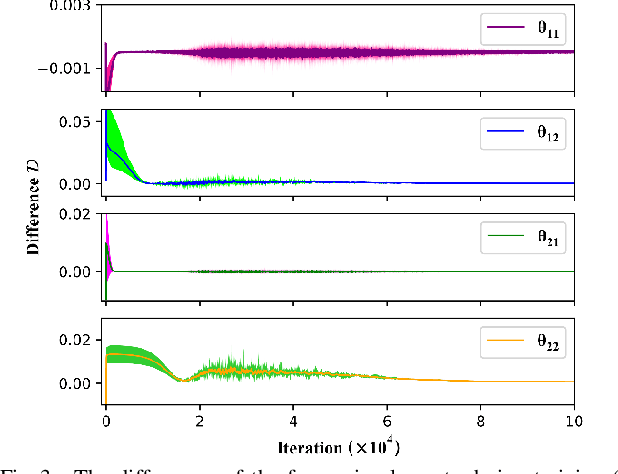
State estimation is critical to control systems, especially when the states cannot be directly measured. This paper presents an approximate optimal filter, which enables to use policy iteration technique to obtain the steady-state gain in linear Gaussian time-invariant systems. This design transforms the optimal filtering problem with minimum mean square error into an optimal control problem, called Approximate Optimal Filtering (AOF) problem. The equivalence holds given certain conditions about initial state distributions and policy formats, in which the system state is the estimation error, control input is the filter gain, and control objective function is the accumulated estimation error. We present a policy iteration algorithm to solve the AOF problem in steady-state. A classic vehicle state estimation problem finally evaluates the approximate filter. The results show that the policy converges to the steady-state Kalman gain, and its accuracy is within 2 %.