Convolutional Bayesian Filtering
Paper and Code
Mar 30, 2024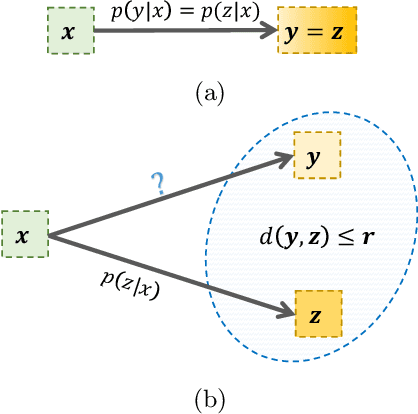
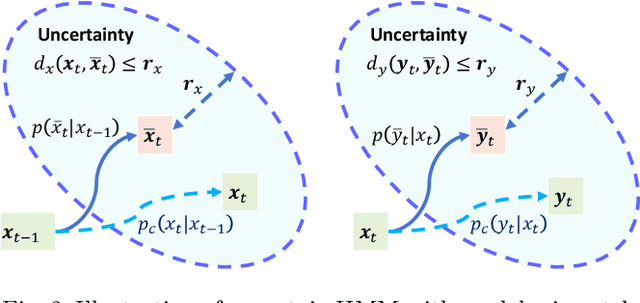
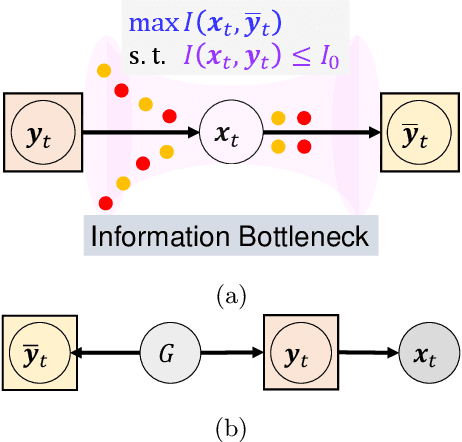
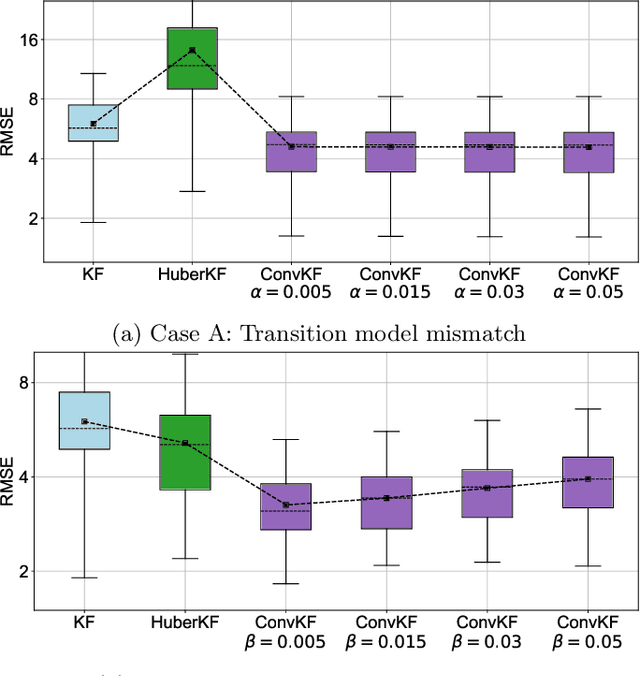
Bayesian filtering serves as the mainstream framework of state estimation in dynamic systems. Its standard version utilizes total probability rule and Bayes' law alternatively, where how to define and compute conditional probability is critical to state distribution inference. Previously, the conditional probability is assumed to be exactly known, which represents a measure of the occurrence probability of one event, given the second event. In this paper, we find that by adding an additional event that stipulates an inequality condition, we can transform the conditional probability into a special integration that is analogous to convolution. Based on this transformation, we show that both transition probability and output probability can be generalized to convolutional forms, resulting in a more general filtering framework that we call convolutional Bayesian filtering. This new framework encompasses standard Bayesian filtering as a special case when the distance metric of the inequality condition is selected as Dirac delta function. It also allows for a more nuanced consideration of model mismatch by choosing different types of inequality conditions. For instance, when the distance metric is defined in a distributional sense, the transition probability and output probability can be approximated by simply rescaling them into fractional powers. Under this framework, a robust version of Kalman filter can be constructed by only altering the noise covariance matrix, while maintaining the conjugate nature of Gaussian distributions. Finally, we exemplify the effectiveness of our approach by reshaping classic filtering algorithms into convolutional versions, including Kalman filter, extended Kalman filter, unscented Kalman filter and particle filter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge