Quantitative Representation of Scenario Difficulty for Autonomous Driving Based on Adversarial Policy Search

Adversarial scenario generation is crucial for autonomous driving testing because it can efficiently simulate various challenge and complex traffic conditions. However, it is difficult to control current existing methods to generate desired scenarios, such as the ones with different conflict levels. Therefore, this paper proposes a data-driven quantitative method to represent scenario difficulty. Compared with rule-based discrete scenario difficulty representation method, the proposed algorithm can achieve continuous difficulty representation. Specifically, the environment agent is introduced, and a reinforcement learning method combined with mechanism knowledge is constructed for policy search to obtain an agent with adversarial behavior. The model parameters of the environment agent at different stages in the training process are extracted to construct a policy group, and then the agents with different adversarial intensity are obtained, which are used to realize data generation in different difficulty scenarios through the simulation environment. Finally, a data-driven scenario difficulty quantitative representation model is constructed, which is used to output the environment agent policy under different difficulties. The result analysis shows that the proposed algorithm can generate reasonable and interpretable scenarios with high discrimination, and can provide quantifiable difficulty representation without any expert logic rule design. The video link is https://www.youtube.com/watch?v=GceGdqAm9Ys.

Integrated Decision and Control at Multi-Lane Intersections with Mixed Traffic Flow

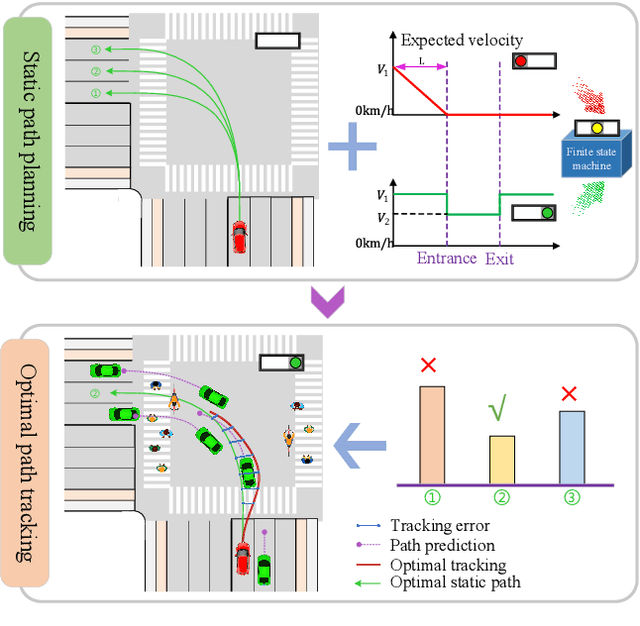
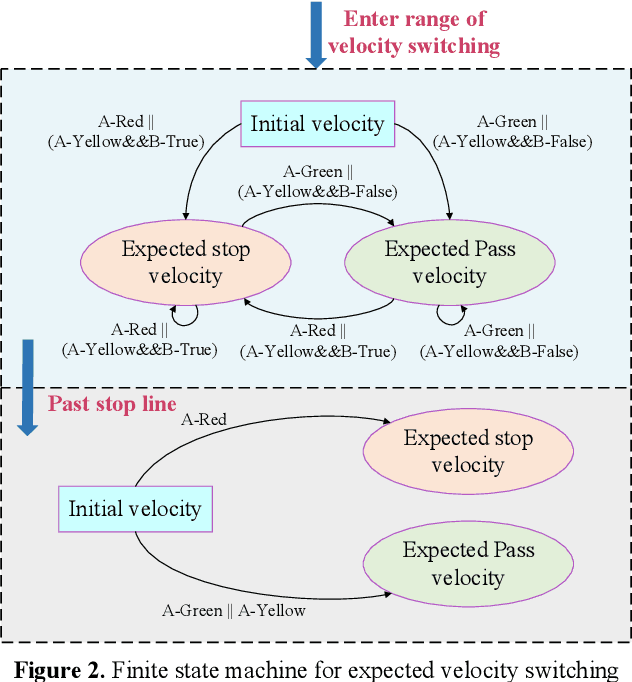
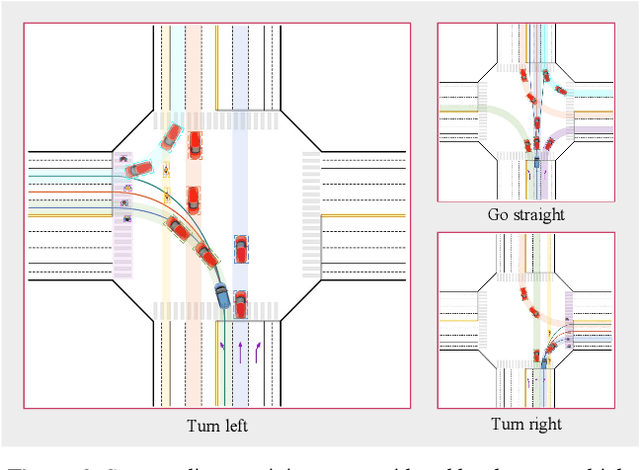
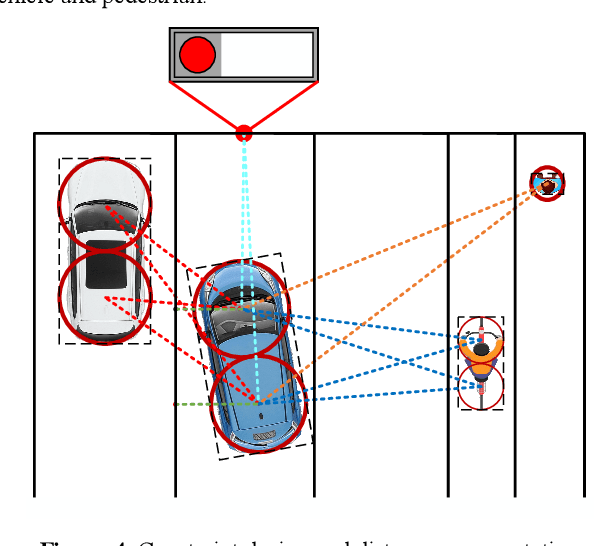
Autonomous driving at intersections is one of the most complicated and accident-prone traffic scenarios, especially with mixed traffic participants such as vehicles, bicycles and pedestrians. The driving policy should make safe decisions to handle the dynamic traffic conditions and meet the requirements of on-board computation. However, most of the current researches focuses on simplified intersections considering only the surrounding vehicles and idealized traffic lights. This paper improves the integrated decision and control framework and develops a learning-based algorithm to deal with complex intersections with mixed traffic flows, which can not only take account of realistic characteristics of traffic lights, but also learn a safe policy under different safety constraints. We first consider different velocity models for green and red lights in the training process and use a finite state machine to handle different modes of light transformation. Then we design different types of distance constraints for vehicles, traffic lights, pedestrians, bicycles respectively and formulize the constrained optimal control problems (OCPs) to be optimized. Finally, reinforcement learning (RL) with value and policy networks is adopted to solve the series of OCPs. In order to verify the safety and efficiency of the proposed method, we design a multi-lane intersection with the existence of large-scale mixed traffic participants and set practical traffic light phases. The simulation results indicate that the trained decision and control policy can well balance safety and tracking performance. Compared with model predictive control (MPC), the computational time is three orders of magnitude lower.

Approximate Optimal Filter for Linear Gaussian Time-invariant Systems

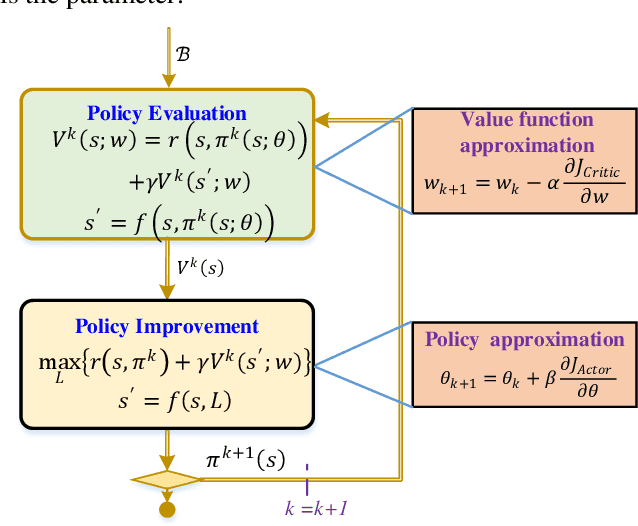
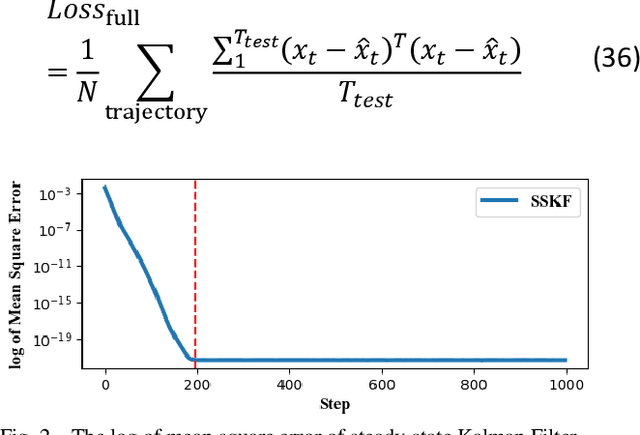
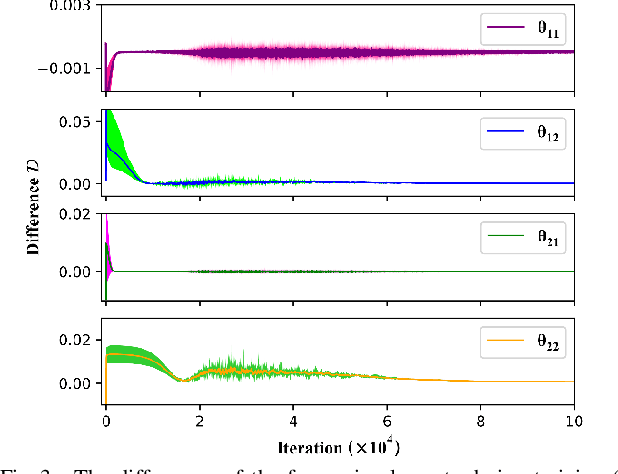
State estimation is critical to control systems, especially when the states cannot be directly measured. This paper presents an approximate optimal filter, which enables to use policy iteration technique to obtain the steady-state gain in linear Gaussian time-invariant systems. This design transforms the optimal filtering problem with minimum mean square error into an optimal control problem, called Approximate Optimal Filtering (AOF) problem. The equivalence holds given certain conditions about initial state distributions and policy formats, in which the system state is the estimation error, control input is the filter gain, and control objective function is the accumulated estimation error. We present a policy iteration algorithm to solve the AOF problem in steady-state. A classic vehicle state estimation problem finally evaluates the approximate filter. The results show that the policy converges to the steady-state Kalman gain, and its accuracy is within 2 %.

Recurrent Model Predictive Control

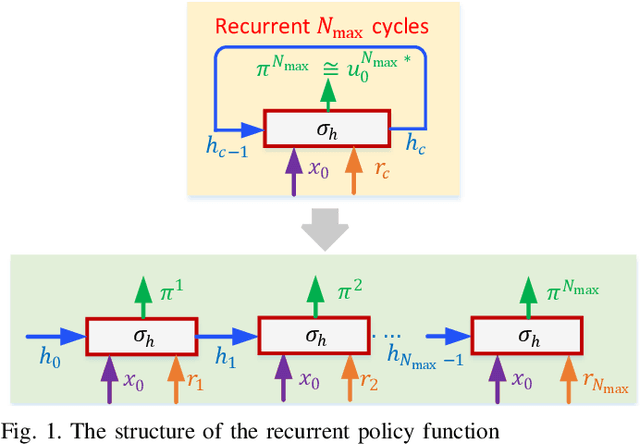
This paper proposes an off-line algorithm, called Recurrent Model Predictive Control (RMPC), to solve general nonlinear finite-horizon optimal control problems. Unlike traditional Model Predictive Control (MPC) algorithms, it can make full use of the current computing resources and adaptively select the longest model prediction horizon. Our algorithm employs a recurrent function to approximate the optimal policy, which maps the system states and reference values directly to the control inputs. The number of prediction steps is equal to the number of recurrent cycles of the learned policy function. With an arbitrary initial policy function, the proposed RMPC algorithm can converge to the optimal policy by directly minimizing the designed loss function. We further prove the convergence and optimality of the RMPC algorithm thorough Bellman optimality principle, and demonstrate its generality and efficiency using two numerical examples.

Model-Based Actor-Critic with Chance Constraint for Stochastic System

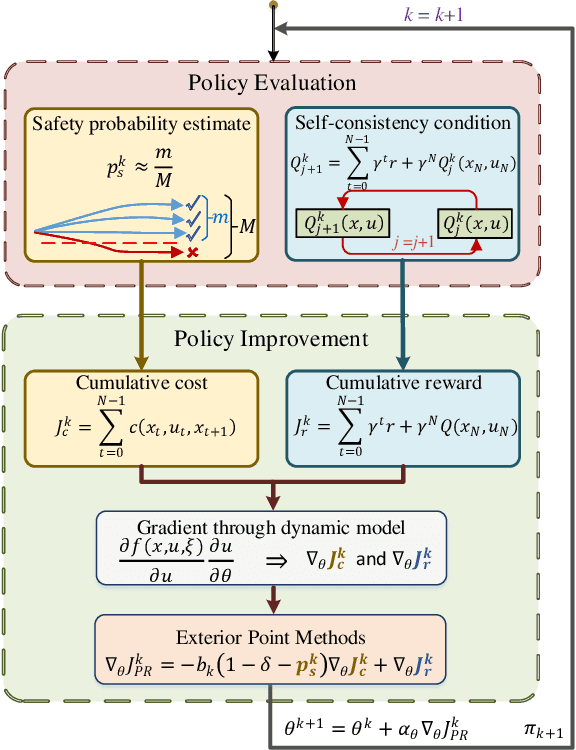
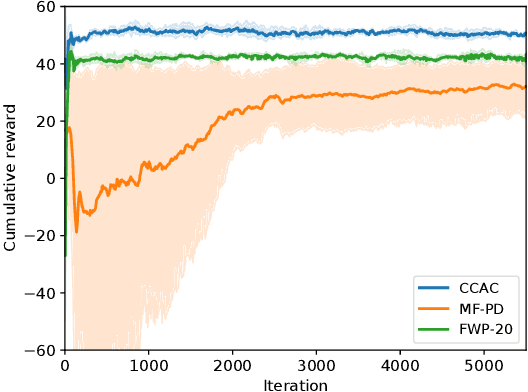
Safety constraints are essential for reinforcement learning (RL) applied in real-world situations. Chance constraints are suitable to represent the safety requirements in stochastic systems. Most existing RL methods with chance constraints have a low convergence rate, and only learn a conservative policy. In this paper, we propose a model-based chance constrained actor-critic (CCAC) algorithm which can efficiently learn a safe and non-conservative policy. Different from existing methods that optimize a conservative lower bound, CCAC directly solves the original chance constrained problems, where the objective function and safe probability is simultaneously optimized with adaptive weights. In order to improve the convergence rate, CCAC utilizes the gradient of dynamic model to accelerate policy optimization. The effectiveness of CCAC is demonstrated by an aggressive car-following task. Experiments indicate that compared with previous methods, CCAC improves the performance by 57.6% while guaranteeing safety, with a five times faster convergence rate.

Ternary Policy Iteration Algorithm for Nonlinear Robust Control

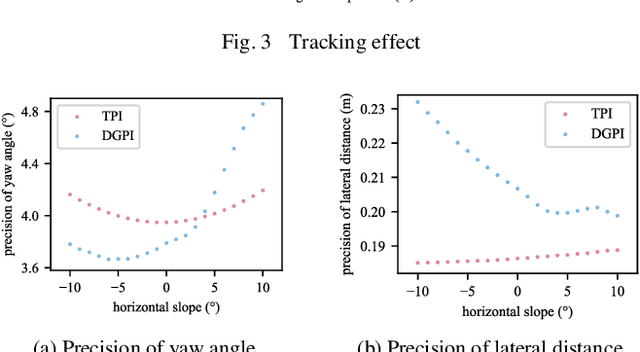
The uncertainties in plant dynamics remain a challenge for nonlinear control problems. This paper develops a ternary policy iteration (TPI) algorithm for solving nonlinear robust control problems with bounded uncertainties. The controller and uncertainty of the system are considered as game players, and the robust control problem is formulated as a two-player zero-sum differential game. In order to solve the differential game, the corresponding Hamilton-Jacobi-Isaacs (HJI) equation is then derived. Three loss functions and three update phases are designed to match the identity equation, minimization and maximization of the HJI equation, respectively. These loss functions are defined by the expectation of the approximate Hamiltonian in a generated state set to prevent operating all the states in the entire state set concurrently. The parameters of value function and policies are directly updated by diminishing the designed loss functions using the gradient descent method. Moreover, zero-initialization can be applied to the parameters of the control policy. The effectiveness of the proposed TPI algorithm is demonstrated through two simulation studies. The simulation results show that the TPI algorithm can converge to the optimal solution for the linear plant, and has high resistance to disturbances for the nonlinear plant.