Positive-Unlabeled Constraint Learning (PUCL) for Inferring Nonlinear Continuous Constraints Functions from Expert Demonstrations

Planning for a wide range of real-world robotic tasks necessitates to know and write all constraints. However, instances exist where these constraints are either unknown or challenging to specify accurately. A possible solution is to infer the unknown constraints from expert demonstration. This paper presents a novel Positive-Unlabeled Constraint Learning (PUCL) algorithm to infer a continuous arbitrary constraint function from demonstration, without requiring prior knowledge of the true constraint parameterization or environmental model as existing works. Within our framework, we treat all data in demonstrations as positive (feasible) data, and learn a control policy to generate potentially infeasible trajectories, which serve as unlabeled data. In each iteration, we first update the policy and then a two-step positive-unlabeled learning procedure is applied, where it first identifies reliable infeasible data using a distance metric, and secondly learns a binary feasibility classifier (i.e., constraint function) from the feasible demonstrations and reliable infeasible data. The proposed framework is flexible to learn complex-shaped constraint boundary and will not mistakenly classify demonstrations as infeasible as previous methods. The effectiveness of the proposed method is verified in three robotic tasks, using a networked policy or a dynamical system policy. It successfully infers and transfers the continuous nonlinear constraints and outperforms other baseline methods in terms of constraint accuracy and policy safety.

Learning General Continuous Constraint from Demonstrations via Positive-Unlabeled Learning

Planning for a wide range of real-world tasks necessitates to know and write all constraints. However, instances exist where these constraints are either unknown or challenging to specify accurately. A possible solution is to infer the unknown constraints from expert demonstration. The majority of prior works limit themselves to learning simple linear constraints, or require strong knowledge of the true constraint parameterization or environmental model. To mitigate these problems, this paper presents a positive-unlabeled (PU) learning approach to infer a continuous, arbitrary and possibly nonlinear, constraint from demonstration. From a PU learning view, We treat all data in demonstrations as positive (feasible) data, and learn a (sub)-optimal policy to generate high-reward-winning but potentially infeasible trajectories, which serve as unlabeled data containing both feasible and infeasible states. Under an assumption on data distribution, a feasible-infeasible classifier (i.e., constraint model) is learned from the two datasets through a postprocessing PU learning technique. The entire method employs an iterative framework alternating between updating the policy, which generates and selects higher-reward policies, and updating the constraint model. Additionally, a memory buffer is introduced to record and reuse samples from previous iterations to prevent forgetting. The effectiveness of the proposed method is validated in two Mujoco environments, successfully inferring continuous nonlinear constraints and outperforming a baseline method in terms of constraint accuracy and policy safety.

Model-based Chance-Constrained Reinforcement Learning via Separated Proportional-Integral Lagrangian

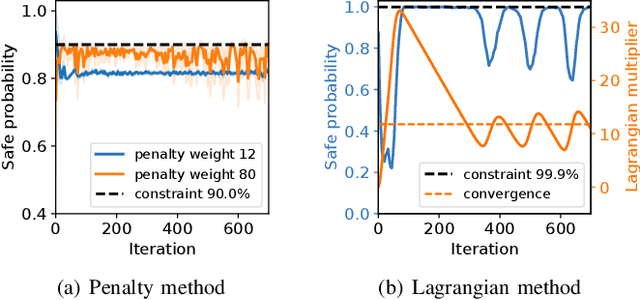
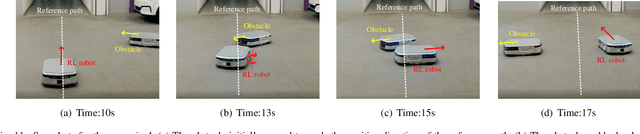
Safety is essential for reinforcement learning (RL) applied in the real world. Adding chance constraints (or probabilistic constraints) is a suitable way to enhance RL safety under uncertainty. Existing chance-constrained RL methods like the penalty methods and the Lagrangian methods either exhibit periodic oscillations or learn an over-conservative or unsafe policy. In this paper, we address these shortcomings by proposing a separated proportional-integral Lagrangian (SPIL) algorithm. We first review the constrained policy optimization process from a feedback control perspective, which regards the penalty weight as the control input and the safe probability as the control output. Based on this, the penalty method is formulated as a proportional controller, and the Lagrangian method is formulated as an integral controller. We then unify them and present a proportional-integral Lagrangian method to get both their merits, with an integral separation technique to limit the integral value in a reasonable range. To accelerate training, the gradient of safe probability is computed in a model-based manner. We demonstrate our method can reduce the oscillations and conservatism of RL policy in a car-following simulation. To prove its practicality, we also apply our method to a real-world mobile robot navigation task, where our robot successfully avoids a moving obstacle with highly uncertain or even aggressive behaviors.

Separated Proportional-Integral Lagrangian for Chance Constrained Reinforcement Learning

Safety is essential for reinforcement learning (RL) applied in real-world tasks like autonomous driving. Chance constraints which guarantee the satisfaction of state constraints at a high probability are suitable to represent the requirements in real-world environment with uncertainty. Existing chance constrained RL methods like the penalty method and the Lagrangian method either exhibit periodic oscillations or cannot satisfy the constraints. In this paper, we address these shortcomings by proposing a separated proportional-integral Lagrangian (SPIL) algorithm. Taking a control perspective, we first interpret the penalty method and the Lagrangian method as proportional feedback and integral feedback control, respectively. Then, a proportional-integral Lagrangian method is proposed to steady learning process while improving safety. To prevent integral overshooting and reduce conservatism, we introduce the integral separation technique inspired by PID control. Finally, an analytical gradient of the chance constraint is utilized for model-based policy optimization. The effectiveness of SPIL is demonstrated by a narrow car-following task. Experiments indicate that compared with previous methods, SPIL improves the performance while guaranteeing safety, with a steady learning process.

Model-Based Actor-Critic with Chance Constraint for Stochastic System

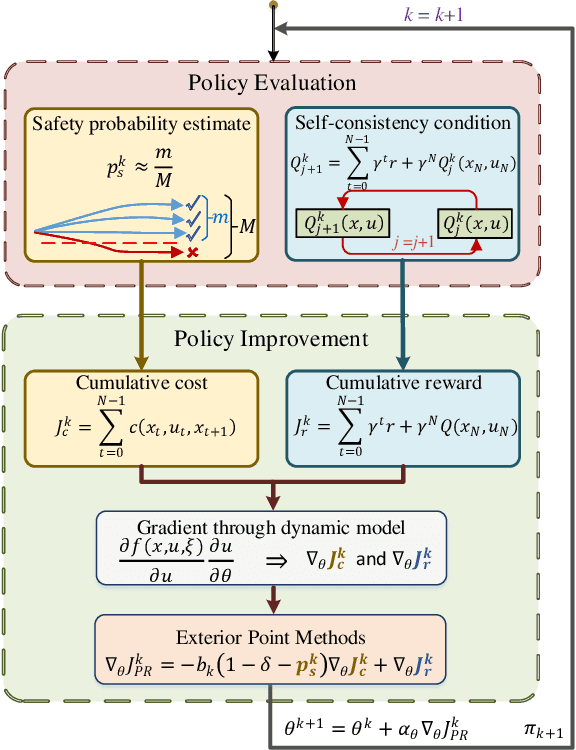
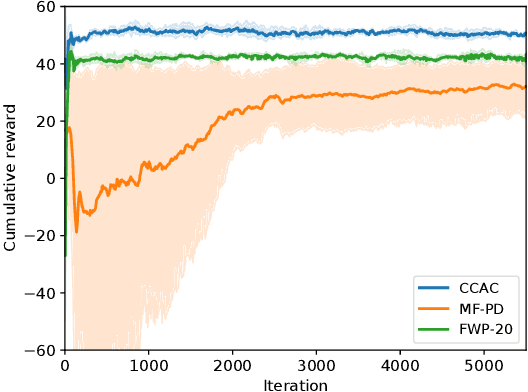
Safety constraints are essential for reinforcement learning (RL) applied in real-world situations. Chance constraints are suitable to represent the safety requirements in stochastic systems. Most existing RL methods with chance constraints have a low convergence rate, and only learn a conservative policy. In this paper, we propose a model-based chance constrained actor-critic (CCAC) algorithm which can efficiently learn a safe and non-conservative policy. Different from existing methods that optimize a conservative lower bound, CCAC directly solves the original chance constrained problems, where the objective function and safe probability is simultaneously optimized with adaptive weights. In order to improve the convergence rate, CCAC utilizes the gradient of dynamic model to accelerate policy optimization. The effectiveness of CCAC is demonstrated by an aggressive car-following task. Experiments indicate that compared with previous methods, CCAC improves the performance by 57.6% while guaranteeing safety, with a five times faster convergence rate.

Mixed Reinforcement Learning with Additive Stochastic Uncertainty

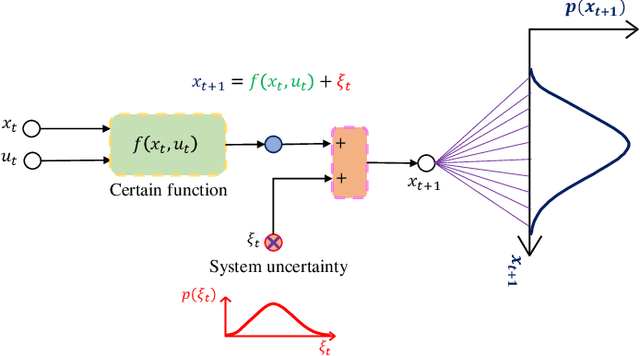
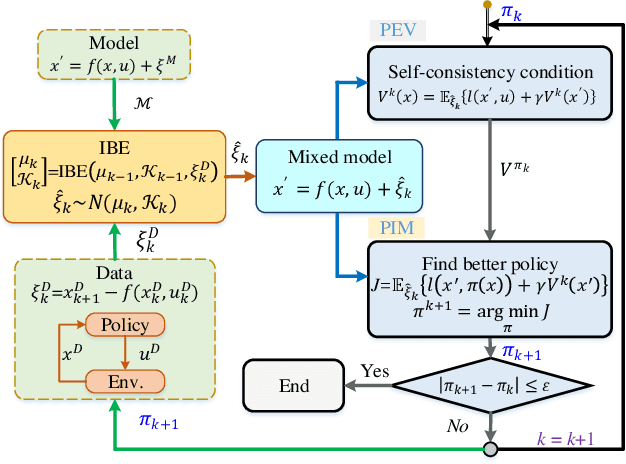
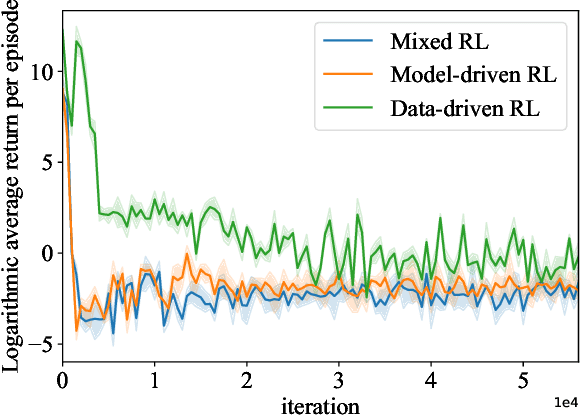
Reinforcement learning (RL) methods often rely on massive exploration data to search optimal policies, and suffer from poor sampling efficiency. This paper presents a mixed reinforcement learning (mixed RL) algorithm by simultaneously using dual representations of environmental dynamics to search the optimal policy with the purpose of improving both learning accuracy and training speed. The dual representations indicate the environmental model and the state-action data: the former can accelerate the learning process of RL, while its inherent model uncertainty generally leads to worse policy accuracy than the latter, which comes from direct measurements of states and actions. In the framework design of the mixed RL, the compensation of the additive stochastic model uncertainty is embedded inside the policy iteration RL framework by using explored state-action data via iterative Bayesian estimator (IBE). The optimal policy is then computed in an iterative way by alternating between policy evaluation (PEV) and policy improvement (PIM). The convergence of the mixed RL is proved using the Bellman's principle of optimality, and the recursive stability of the generated policy is proved via the Lyapunov's direct method. The effectiveness of the mixed RL is demonstrated by a typical optimal control problem of stochastic non-affine nonlinear systems (i.e., double lane change task with an automated vehicle).