On the Optimization Landscape of Dynamic Output Feedback: A Case Study for Linear Quadratic Regulator
Paper and Code
Sep 12, 2022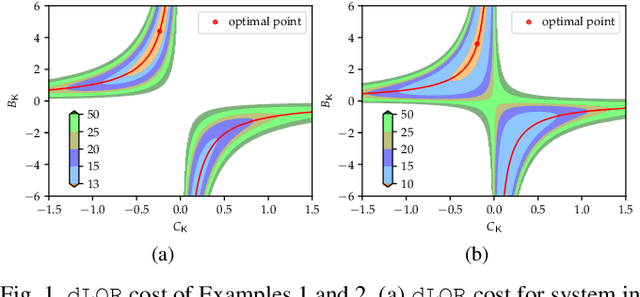
The convergence of policy gradient algorithms in reinforcement learning hinges on the optimization landscape of the underlying optimal control problem. Theoretical insights into these algorithms can often be acquired from analyzing those of linear quadratic control. However, most of the existing literature only considers the optimization landscape for static full-state or output feedback policies (controllers). We investigate the more challenging case of dynamic output-feedback policies for linear quadratic regulation (abbreviated as dLQR), which is prevalent in practice but has a rather complicated optimization landscape. We first show how the dLQR cost varies with the coordinate transformation of the dynamic controller and then derive the optimal transformation for a given observable stabilizing controller. At the core of our results is the uniqueness of the stationary point of dLQR when it is observable, which is in a concise form of an observer-based controller with the optimal similarity transformation. These results shed light on designing efficient algorithms for general decision-making problems with partially observed information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge