Diversifying AI: Towards Creative Chess with AlphaZero

In recent years, Artificial Intelligence (AI) systems have surpassed human intelligence in a variety of computational tasks. However, AI systems, like humans, make mistakes, have blind spots, hallucinate, and struggle to generalize to new situations. This work explores whether AI can benefit from creative decision-making mechanisms when pushed to the limits of its computational rationality. In particular, we investigate whether a team of diverse AI systems can outperform a single AI in challenging tasks by generating more ideas as a group and then selecting the best ones. We study this question in the game of chess, the so-called drosophila of AI. We build on AlphaZero (AZ) and extend it to represent a league of agents via a latent-conditioned architecture, which we call AZ_db. We train AZ_db to generate a wider range of ideas using behavioral diversity techniques and select the most promising ones with sub-additive planning. Our experiments suggest that AZ_db plays chess in diverse ways, solves more puzzles as a group and outperforms a more homogeneous team. Notably, AZ_db solves twice as many challenging puzzles as AZ, including the challenging Penrose positions. When playing chess from different openings, we notice that players in AZ_db specialize in different openings, and that selecting a player for each opening using sub-additive planning results in a 50 Elo improvement over AZ. Our findings suggest that diversity bonuses emerge in teams of AI agents, just as they do in teams of humans and that diversity is a valuable asset in solving computationally hard problems.

APART: Diverse Skill Discovery using All Pairs with Ascending Reward and DropouT

We study diverse skill discovery in reward-free environments, aiming to discover all possible skills in simple grid-world environments where prior methods have struggled to succeed. This problem is formulated as mutual training of skills using an intrinsic reward and a discriminator trained to predict a skill given its trajectory. Our initial solution replaces the standard one-vs-all (softmax) discriminator with a one-vs-one (all pairs) discriminator and combines it with a novel intrinsic reward function and a dropout regularization technique. The combined approach is named APART: Diverse Skill Discovery using All Pairs with Ascending Reward and Dropout. We demonstrate that APART discovers all the possible skills in grid worlds with remarkably fewer samples than previous works. Motivated by the empirical success of APART, we further investigate an even simpler algorithm that achieves maximum skills by altering VIC, rescaling its intrinsic reward, and tuning the temperature of its softmax discriminator. We believe our findings shed light on the crucial factors underlying success of skill discovery algorithms in reinforcement learning.

Optimism and Adaptivity in Policy Optimization

We work towards a unifying paradigm for accelerating policy optimization methods in reinforcement learning (RL) through \emph{optimism} \& \emph{adaptivity}. Leveraging the deep connection between policy iteration and policy gradient methods, we recast seemingly unrelated policy optimization algorithms as the repeated application of two interleaving steps (i) an \emph{optimistic policy improvement operator} maps a prior policy $\pi_t$ to a hypothesis $\pi_{t+1}$ using a \emph{gradient ascent prediction}, followed by (ii) a \emph{hindsight adaptation} of the optimistic prediction based on a partial evaluation of the performance of $\pi_{t+1}$. We use this shared lens to jointly express other well-known algorithms, including soft and optimistic policy iteration, natural actor-critic methods, model-based policy improvement based on forward search, and meta-learning algorithms. By doing so, we shed light on collective theoretical properties related to acceleration via optimism \& adaptivity. Building on these insights, we design an \emph{adaptive \& optimistic policy gradient} algorithm via meta-gradient learning, and empirically highlight several design choices pertaining to optimism, in an illustrative task.

Discovering Attention-Based Genetic Algorithms via Meta-Black-Box Optimization

Genetic algorithms constitute a family of black-box optimization algorithms, which take inspiration from the principles of biological evolution. While they provide a general-purpose tool for optimization, their particular instantiations can be heuristic and motivated by loose biological intuition. In this work we explore a fundamentally different approach: Given a sufficiently flexible parametrization of the genetic operators, we discover entirely new genetic algorithms in a data-driven fashion. More specifically, we parametrize selection and mutation rate adaptation as cross- and self-attention modules and use Meta-Black-Box-Optimization to evolve their parameters on a set of diverse optimization tasks. The resulting Learned Genetic Algorithm outperforms state-of-the-art adaptive baseline genetic algorithms and generalizes far beyond its meta-training settings. The learned algorithm can be applied to previously unseen optimization problems, search dimensions & evaluation budgets. We conduct extensive analysis of the discovered operators and provide ablation experiments, which highlight the benefits of flexible module parametrization and the ability to transfer (`plug-in') the learned operators to conventional genetic algorithms.

ReLOAD: Reinforcement Learning with Optimistic Ascent-Descent for Last-Iterate Convergence in Constrained MDPs

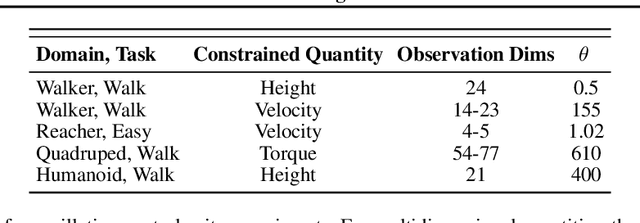
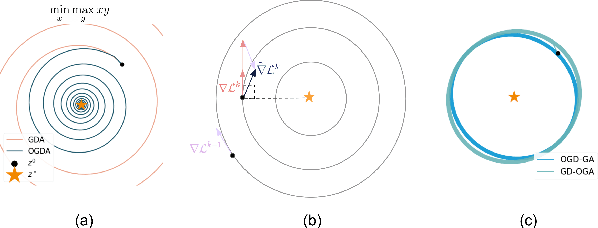
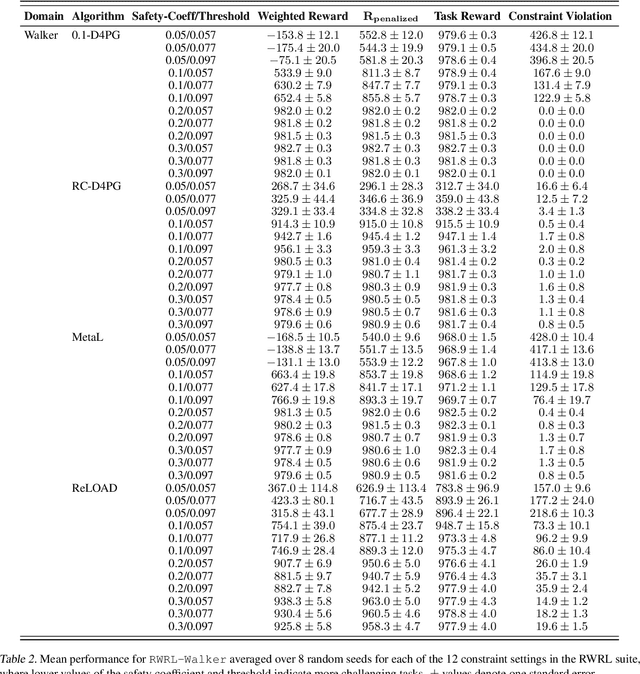
In recent years, Reinforcement Learning (RL) has been applied to real-world problems with increasing success. Such applications often require to put constraints on the agent's behavior. Existing algorithms for constrained RL (CRL) rely on gradient descent-ascent, but this approach comes with a caveat. While these algorithms are guaranteed to converge on average, they do not guarantee last-iterate convergence, i.e., the current policy of the agent may never converge to the optimal solution. In practice, it is often observed that the policy alternates between satisfying the constraints and maximizing the reward, rarely accomplishing both objectives simultaneously. Here, we address this problem by introducing Reinforcement Learning with Optimistic Ascent-Descent (ReLOAD), a principled CRL method with guaranteed last-iterate convergence. We demonstrate its empirical effectiveness on a wide variety of CRL problems including discrete MDPs and continuous control. In the process we establish a benchmark of challenging CRL problems.

Optimistic Meta-Gradients

We study the connection between gradient-based meta-learning and convex op-timisation. We observe that gradient descent with momentum is a special case of meta-gradients, and building on recent results in optimisation, we prove convergence rates for meta-learning in the single task setting. While a meta-learned update rule can yield faster convergence up to constant factor, it is not sufficient for acceleration. Instead, some form of optimism is required. We show that optimism in meta-learning can be captured through Bootstrapped Meta-Gradients (Flennerhag et al., 2022), providing deeper insight into its underlying mechanics.

POMRL: No-Regret Learning-to-Plan with Increasing Horizons

We study the problem of planning under model uncertainty in an online meta-reinforcement learning (RL) setting where an agent is presented with a sequence of related tasks with limited interactions per task. The agent can use its experience in each task and across tasks to estimate both the transition model and the distribution over tasks. We propose an algorithm to meta-learn the underlying structure across tasks, utilize it to plan in each task, and upper-bound the regret of the planning loss. Our bound suggests that the average regret over tasks decreases as the number of tasks increases and as the tasks are more similar. In the classical single-task setting, it is known that the planning horizon should depend on the estimated model's accuracy, that is, on the number of samples within task. We generalize this finding to meta-RL and study this dependence of planning horizons on the number of tasks. Based on our theoretical findings, we derive heuristics for selecting slowly increasing discount factors, and we validate its significance empirically.

Discovering Evolution Strategies via Meta-Black-Box Optimization

Optimizing functions without access to gradients is the remit of black-box methods such as evolution strategies. While highly general, their learning dynamics are often times heuristic and inflexible - exactly the limitations that meta-learning can address. Hence, we propose to discover effective update rules for evolution strategies via meta-learning. Concretely, our approach employs a search strategy parametrized by a self-attention-based architecture, which guarantees the update rule is invariant to the ordering of the candidate solutions. We show that meta-evolving this system on a small set of representative low-dimensional analytic optimization problems is sufficient to discover new evolution strategies capable of generalizing to unseen optimization problems, population sizes and optimization horizons. Furthermore, the same learned evolution strategy can outperform established neuroevolution baselines on supervised and continuous control tasks. As additional contributions, we ablate the individual neural network components of our method; reverse engineer the learned strategy into an explicit heuristic form, which remains highly competitive; and show that it is possible to self-referentially train an evolution strategy from scratch, with the learned update rule used to drive the outer meta-learning loop.

Meta-Gradients in Non-Stationary Environments

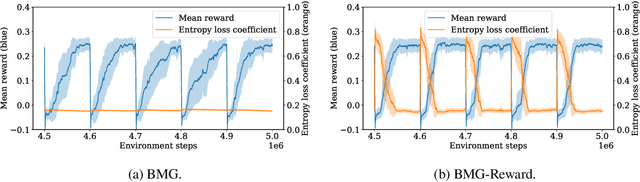
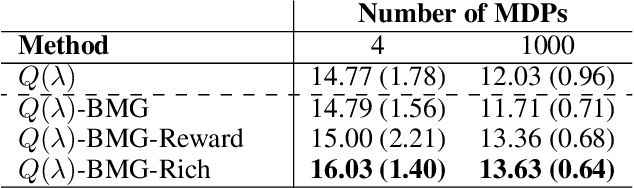
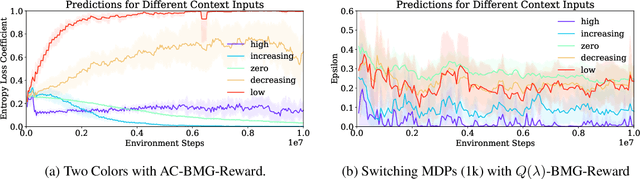
Meta-gradient methods (Xu et al., 2018; Zahavy et al., 2020) offer a promising solution to the problem of hyperparameter selection and adaptation in non-stationary reinforcement learning problems. However, the properties of meta-gradients in such environments have not been systematically studied. In this work, we bring new clarity to meta-gradients in non-stationary environments. Concretely, we ask: (i) how much information should be given to the learned optimizers, so as to enable faster adaptation and generalization over a lifetime, (ii) what meta-optimizer functions are learned in this process, and (iii) whether meta-gradient methods provide a bigger advantage in highly non-stationary environments. To study the effect of information provided to the meta-optimizer, as in recent works (Flennerhag et al., 2021; Almeida et al., 2021), we replace the tuned meta-parameters of fixed update rules with learned meta-parameter functions of selected context features. The context features carry information about agent performance and changes in the environment and hence can inform learned meta-parameter schedules. We find that adding more contextual information is generally beneficial, leading to faster adaptation of meta-parameter values and increased performance over a lifetime. We support these results with a qualitative analysis of resulting meta-parameter schedules and learned functions of context features. Lastly, we find that without context, meta-gradients do not provide a consistent advantage over the baseline in highly non-stationary environments. Our findings suggest that contextualizing meta-gradients can play a pivotal role in extracting high performance from meta-gradients in non-stationary settings.

Discovering Policies with DOMiNO: Diversity Optimization Maintaining Near Optimality

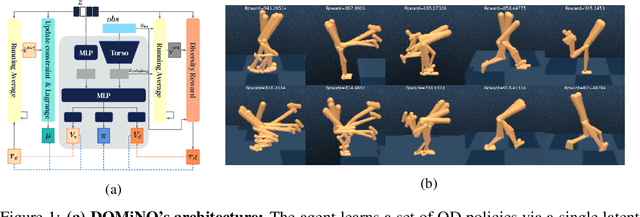
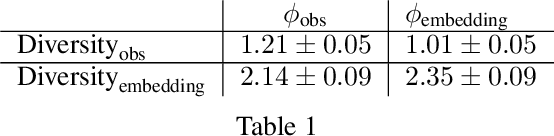
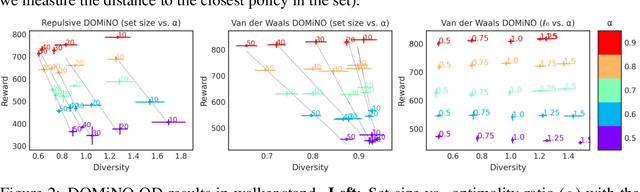
Finding different solutions to the same problem is a key aspect of intelligence associated with creativity and adaptation to novel situations. In reinforcement learning, a set of diverse policies can be useful for exploration, transfer, hierarchy, and robustness. We propose DOMiNO, a method for Diversity Optimization Maintaining Near Optimality. We formalize the problem as a Constrained Markov Decision Process where the objective is to find diverse policies, measured by the distance between the state occupancies of the policies in the set, while remaining near-optimal with respect to the extrinsic reward. We demonstrate that the method can discover diverse and meaningful behaviors in various domains, such as different locomotion patterns in the DeepMind Control Suite. We perform extensive analysis of our approach, compare it with other multi-objective baselines, demonstrate that we can control both the quality and the diversity of the set via interpretable hyperparameters, and show that the discovered set is robust to perturbations.