Kevin Waugh
Diversifying AI: Towards Creative Chess with AlphaZero
Aug 29, 2023



Abstract:In recent years, Artificial Intelligence (AI) systems have surpassed human intelligence in a variety of computational tasks. However, AI systems, like humans, make mistakes, have blind spots, hallucinate, and struggle to generalize to new situations. This work explores whether AI can benefit from creative decision-making mechanisms when pushed to the limits of its computational rationality. In particular, we investigate whether a team of diverse AI systems can outperform a single AI in challenging tasks by generating more ideas as a group and then selecting the best ones. We study this question in the game of chess, the so-called drosophila of AI. We build on AlphaZero (AZ) and extend it to represent a league of agents via a latent-conditioned architecture, which we call AZ_db. We train AZ_db to generate a wider range of ideas using behavioral diversity techniques and select the most promising ones with sub-additive planning. Our experiments suggest that AZ_db plays chess in diverse ways, solves more puzzles as a group and outperforms a more homogeneous team. Notably, AZ_db solves twice as many challenging puzzles as AZ, including the challenging Penrose positions. When playing chess from different openings, we notice that players in AZ_db specialize in different openings, and that selecting a player for each opening using sub-additive planning results in a 50 Elo improvement over AZ. Our findings suggest that diversity bonuses emerge in teams of AI agents, just as they do in teams of humans and that diversity is a valuable asset in solving computationally hard problems.
Player of Games
Dec 06, 2021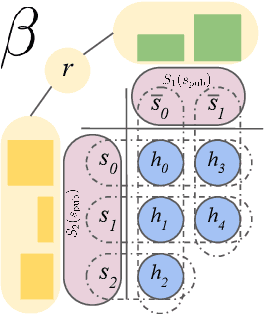

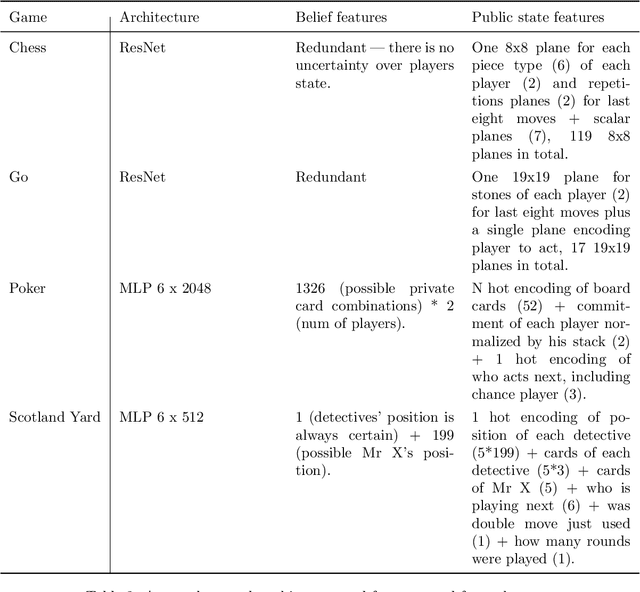
Abstract:Games have a long history of serving as a benchmark for progress in artificial intelligence. Recently, approaches using search and learning have shown strong performance across a set of perfect information games, and approaches using game-theoretic reasoning and learning have shown strong performance for specific imperfect information poker variants. We introduce Player of Games, a general-purpose algorithm that unifies previous approaches, combining guided search, self-play learning, and game-theoretic reasoning. Player of Games is the first algorithm to achieve strong empirical performance in large perfect and imperfect information games -- an important step towards truly general algorithms for arbitrary environments. We prove that Player of Games is sound, converging to perfect play as available computation time and approximation capacity increases. Player of Games reaches strong performance in chess and Go, beats the strongest openly available agent in heads-up no-limit Texas hold'em poker (Slumbot), and defeats the state-of-the-art agent in Scotland Yard, an imperfect information game that illustrates the value of guided search, learning, and game-theoretic reasoning.
Solving Large Extensive-Form Games with Strategy Constraints
Sep 20, 2018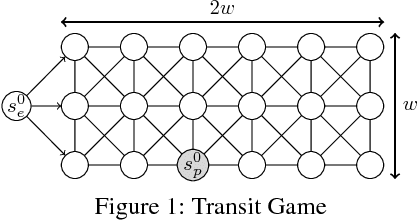
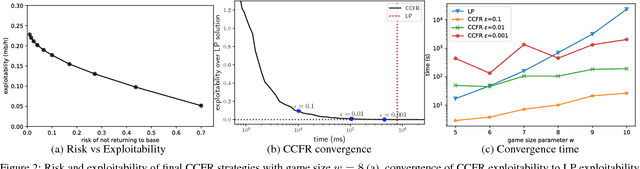
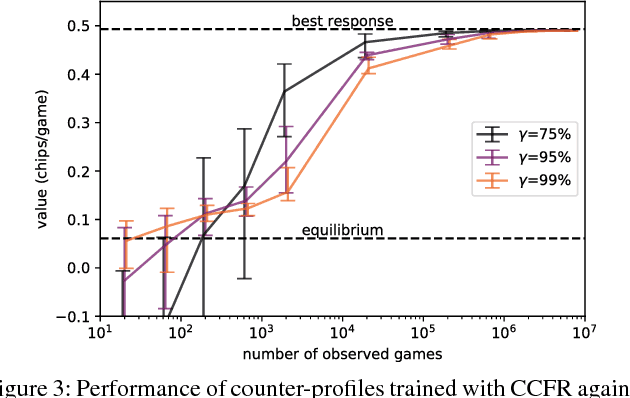
Abstract:Extensive-form games are a common model for multiagent interactions with imperfect information. In two-player zero-sum games, the typical solution concept is a Nash equilibrium over the unconstrained strategy set for each player. In many situations, however, we would like to constrain the set of possible strategies. For example, constraints are a natural way to model limited resources, risk mitigation, safety, consistency with past observations of behavior, or other secondary objectives for an agent. In small games, optimal strategies under linear constraints can be found by solving a linear program; however, state-of-the-art algorithms for solving large games cannot handle general constraints. In this work we introduce a generalized form of Counterfactual Regret Minimization that provably finds optimal strategies under any feasible set of convex constraints. We demonstrate the effectiveness of our algorithm for finding strategies that mitigate risk in security games, and for opponent modeling in poker games when given only partial observations of private information.
Theoretical and Practical Advances on Smoothing for Extensive-Form Games
May 09, 2017


Abstract:Sparse iterative methods, in particular first-order methods, are known to be among the most effective in solving large-scale two-player zero-sum extensive-form games. The convergence rates of these methods depend heavily on the properties of the distance-generating function that they are based on. We investigate the acceleration of first-order methods for solving extensive-form games through better design of the dilated entropy function---a class of distance-generating functions related to the domains associated with the extensive-form games. By introducing a new weighting scheme for the dilated entropy function, we develop the first distance-generating function for the strategy spaces of sequential games that has no dependence on the branching factor of the player. This result improves the convergence rate of several first-order methods by a factor of $\Omega(b^dd)$, where $b$ is the branching factor of the player, and $d$ is the depth of the game tree. Thus far, counterfactual regret minimization methods have been faster in practice, and more popular, than first-order methods despite their theoretically inferior convergence rates. Using our new weighting scheme and practical tuning we show that, for the first time, the excessive gap technique can be made faster than the fastest counterfactual regret minimization algorithm, CFR+, in practice.
DeepStack: Expert-Level Artificial Intelligence in No-Limit Poker
Mar 03, 2017Abstract:Artificial intelligence has seen several breakthroughs in recent years, with games often serving as milestones. A common feature of these games is that players have perfect information. Poker is the quintessential game of imperfect information, and a longstanding challenge problem in artificial intelligence. We introduce DeepStack, an algorithm for imperfect information settings. It combines recursive reasoning to handle information asymmetry, decomposition to focus computation on the relevant decision, and a form of intuition that is automatically learned from self-play using deep learning. In a study involving 44,000 hands of poker, DeepStack defeated with statistical significance professional poker players in heads-up no-limit Texas hold'em. The approach is theoretically sound and is shown to produce more difficult to exploit strategies than prior approaches.
Solving Games with Functional Regret Estimation
Dec 31, 2014


Abstract:We propose a novel online learning method for minimizing regret in large extensive-form games. The approach learns a function approximator online to estimate the regret for choosing a particular action. A no-regret algorithm uses these estimates in place of the true regrets to define a sequence of policies. We prove the approach sound by providing a bound relating the quality of the function approximation and regret of the algorithm. A corollary being that the method is guaranteed to converge to a Nash equilibrium in self-play so long as the regrets are ultimately realizable by the function approximator. Our technique can be understood as a principled generalization of existing work on abstraction in large games; in our work, both the abstraction as well as the equilibrium are learned during self-play. We demonstrate empirically the method achieves higher quality strategies than state-of-the-art abstraction techniques given the same resources.
A Unified View of Large-scale Zero-sum Equilibrium Computation
Nov 18, 2014Abstract:The task of computing approximate Nash equilibria in large zero-sum extensive-form games has received a tremendous amount of attention due mainly to the Annual Computer Poker Competition. Immediately after its inception, two competing and seemingly different approaches emerged---one an application of no-regret online learning, the other a sophisticated gradient method applied to a convex-concave saddle-point formulation. Since then, both approaches have grown in relative isolation with advancements on one side not effecting the other. In this paper, we rectify this by dissecting and, in a sense, unify the two views.
Computational Rationalization: The Inverse Equilibrium Problem
Aug 15, 2013



Abstract:Modeling the purposeful behavior of imperfect agents from a small number of observations is a challenging task. When restricted to the single-agent decision-theoretic setting, inverse optimal control techniques assume that observed behavior is an approximately optimal solution to an unknown decision problem. These techniques learn a utility function that explains the example behavior and can then be used to accurately predict or imitate future behavior in similar observed or unobserved situations. In this work, we consider similar tasks in competitive and cooperative multi-agent domains. Here, unlike single-agent settings, a player cannot myopically maximize its reward; it must speculate on how the other agents may act to influence the game's outcome. Employing the game-theoretic notion of regret and the principle of maximum entropy, we introduce a technique for predicting and generalizing behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge