Low-Variance and Zero-Variance Baselines for Extensive-Form Games

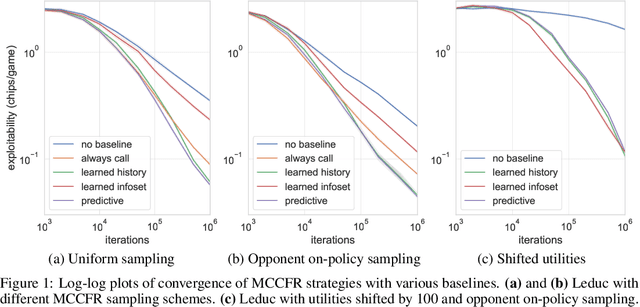
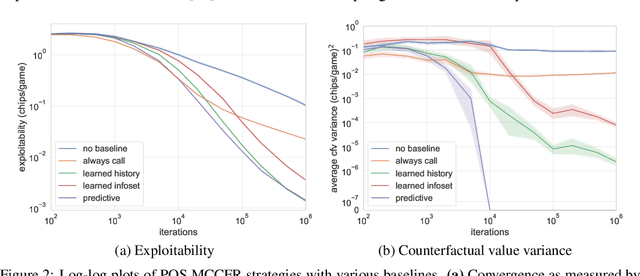
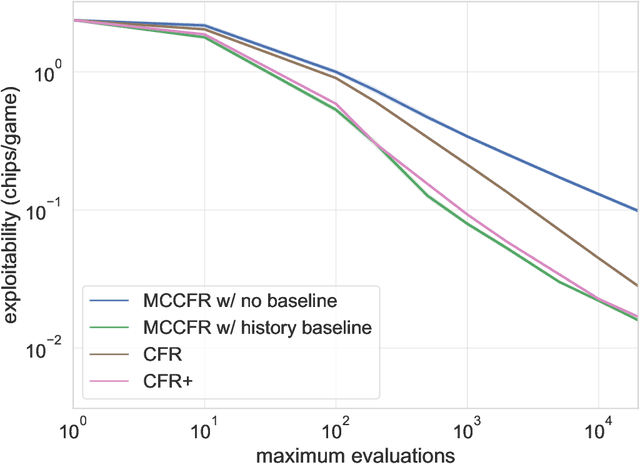
Extensive-form games (EFGs) are a common model of multi-agent interactions with imperfect information. State-of-the-art algorithms for solving these games typically perform full walks of the game tree that can prove prohibitively slow in large games. Alternatively, sampling-based methods such as Monte Carlo Counterfactual Regret Minimization walk one or more trajectories through the tree, touching only a fraction of the nodes on each iteration, at the expense of requiring more iterations to converge due to the variance of sampled values. In this paper, we extend recent work that uses baseline estimates to reduce this variance. We introduce a framework of baseline-corrected values in EFGs that generalizes the previous work. Within our framework, we propose new baseline functions that result in significantly reduced variance compared to existing techniques. We show that one particular choice of such a function --- predictive baseline --- is provably optimal under certain sampling schemes. This allows for efficient computation of zero-variance value estimates even along sampled trajectories.

Solving Large Extensive-Form Games with Strategy Constraints

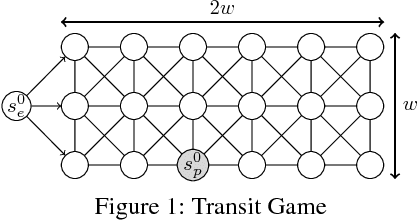
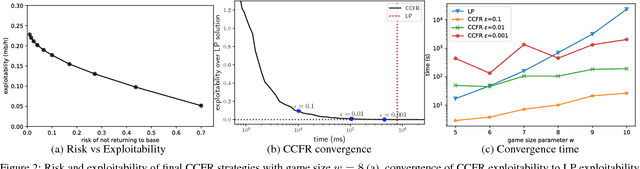
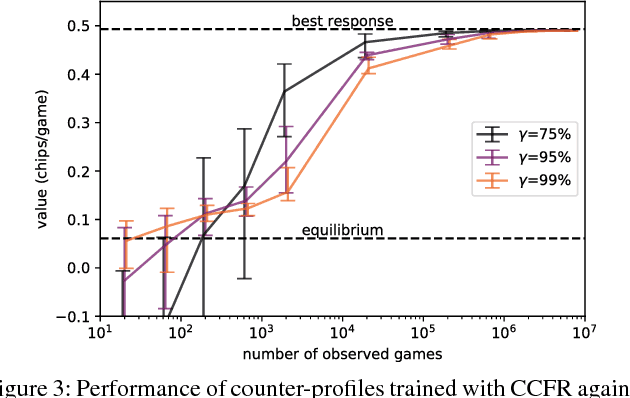
Extensive-form games are a common model for multiagent interactions with imperfect information. In two-player zero-sum games, the typical solution concept is a Nash equilibrium over the unconstrained strategy set for each player. In many situations, however, we would like to constrain the set of possible strategies. For example, constraints are a natural way to model limited resources, risk mitigation, safety, consistency with past observations of behavior, or other secondary objectives for an agent. In small games, optimal strategies under linear constraints can be found by solving a linear program; however, state-of-the-art algorithms for solving large games cannot handle general constraints. In this work we introduce a generalized form of Counterfactual Regret Minimization that provably finds optimal strategies under any feasible set of convex constraints. We demonstrate the effectiveness of our algorithm for finding strategies that mitigate risk in security games, and for opponent modeling in poker games when given only partial observations of private information.

DeepStack: Expert-Level Artificial Intelligence in No-Limit Poker

Artificial intelligence has seen several breakthroughs in recent years, with games often serving as milestones. A common feature of these games is that players have perfect information. Poker is the quintessential game of imperfect information, and a longstanding challenge problem in artificial intelligence. We introduce DeepStack, an algorithm for imperfect information settings. It combines recursive reasoning to handle information asymmetry, decomposition to focus computation on the relevant decision, and a form of intuition that is automatically learned from self-play using deep learning. In a study involving 44,000 hands of poker, DeepStack defeated with statistical significance professional poker players in heads-up no-limit Texas hold'em. The approach is theoretically sound and is shown to produce more difficult to exploit strategies than prior approaches.