Distributionally Robust Skeleton Learning of Discrete Bayesian Networks

We consider the problem of learning the exact skeleton of general discrete Bayesian networks from potentially corrupted data. Building on distributionally robust optimization and a regression approach, we propose to optimize the most adverse risk over a family of distributions within bounded Wasserstein distance or KL divergence to the empirical distribution. The worst-case risk accounts for the effect of outliers. The proposed approach applies for general categorical random variables without assuming faithfulness, an ordinal relationship or a specific form of conditional distribution. We present efficient algorithms and show the proposed methods are closely related to the standard regularized regression approach. Under mild assumptions, we derive non-asymptotic guarantees for successful structure learning with logarithmic sample complexities for bounded-degree graphs. Numerical study on synthetic and real datasets validates the effectiveness of our method. Code is available at https://github.com/DanielLeee/drslbn.

Consistent Robust Adversarial Prediction for General Multiclass Classification

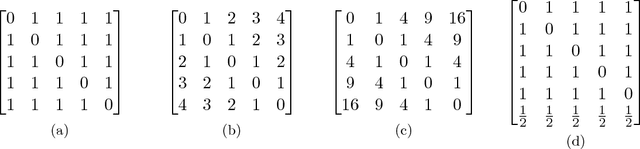
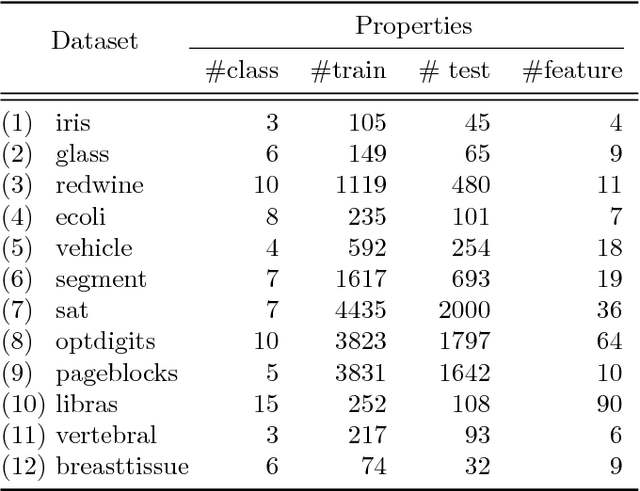
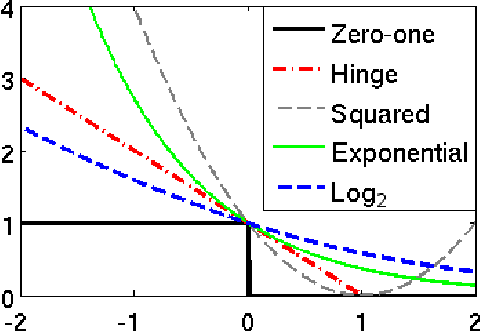
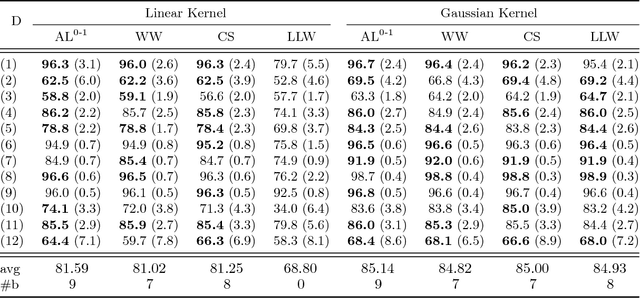
We propose a robust adversarial prediction framework for general multiclass classification. Our method seeks predictive distributions that robustly optimize non-convex and non-continuous multiclass loss metrics against the worst-case conditional label distributions (the adversarial distributions) that (approximately) match the statistics of the training data. Although the optimized loss metrics are non-convex and non-continuous, the dual formulation of the framework is a convex optimization problem that can be recast as a risk minimization model with a prescribed convex surrogate loss we call the adversarial surrogate loss. We show that the adversarial surrogate losses fill an existing gap in surrogate loss construction for general multiclass classification problems, by simultaneously aligning better with the original multiclass loss, guaranteeing Fisher consistency, enabling a way to incorporate rich feature spaces via the kernel trick, and providing competitive performance in practice.

Distributionally Robust Graphical Models

In many structured prediction problems, complex relationships between variables are compactly defined using graphical structures. The most prevalent graphical prediction methods---probabilistic graphical models and large margin methods---have their own distinct strengths but also possess significant drawbacks. Conditional random fields (CRFs) are Fisher consistent, but they do not permit integration of customized loss metrics into their learning process. Large-margin models, such as structured support vector machines (SSVMs), have the flexibility to incorporate customized loss metrics, but lack Fisher consistency guarantees. We present adversarial graphical models (AGM), a distributionally robust approach for constructing a predictor that performs robustly for a class of data distributions defined using a graphical structure. Our approach enjoys both the flexibility of incorporating customized loss metrics into its design as well as the statistical guarantee of Fisher consistency. We present exact learning and prediction algorithms for AGM with time complexity similar to existing graphical models and show the practical benefits of our approach with experiments.

Kernel Robust Bias-Aware Prediction under Covariate Shift

Under covariate shift, training (source) data and testing (target) data differ in input space distribution, but share the same conditional label distribution. This poses a challenging machine learning task. Robust Bias-Aware (RBA) prediction provides the conditional label distribution that is robust to the worstcase logarithmic loss for the target distribution while matching feature expectation constraints from the source distribution. However, employing RBA with insufficient feature constraints may result in high certainty predictions for much of the source data, while leaving too much uncertainty for target data predictions. To overcome this issue, we extend the representer theorem to the RBA setting, enabling minimization of regularized expected target risk by a reweighted kernel expectation under the source distribution. By applying kernel methods, we establish consistency guarantees and demonstrate better performance of the RBA classifier than competing methods on synthetically biased UCI datasets as well as datasets that have natural covariate shift.

Robust Covariate Shift Prediction with General Losses and Feature Views

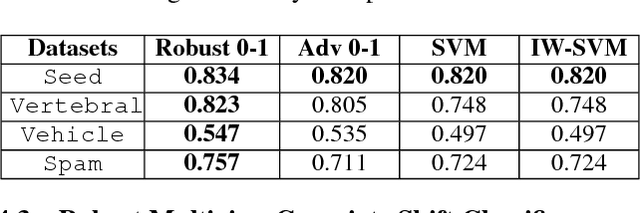
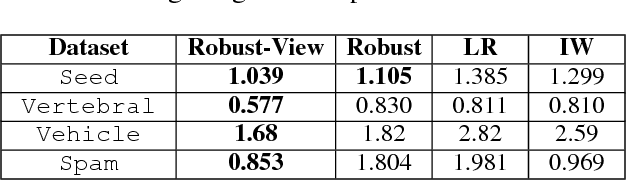
Covariate shift relaxes the widely-employed independent and identically distributed (IID) assumption by allowing different training and testing input distributions. Unfortunately, common methods for addressing covariate shift by trying to remove the bias between training and testing distributions using importance weighting often provide poor performance guarantees in theory and unreliable predictions with high variance in practice. Recently developed methods that construct a predictor that is inherently robust to the difficulties of learning under covariate shift are restricted to minimizing logloss and can be too conservative when faced with high-dimensional learning tasks. We address these limitations in two ways: by robustly minimizing various loss functions, including non-convex ones, under the testing distribution; and by separately shaping the influence of covariate shift according to different feature-based views of the relationship between input variables and example labels. These generalizations make robust covariate shift prediction applicable to more task scenarios. We demonstrate the benefits on classification under covariate shift tasks.

Adversarial Structured Prediction for Multivariate Measures

Many predicted structured objects (e.g., sequences, matchings, trees) are evaluated using the F-score, alignment error rate (AER), or other multivariate performance measures. Since inductively optimizing these measures using training data is typically computationally difficult, empirical risk minimization of surrogate losses is employed, using, e.g., the hinge loss for (structured) support vector machines. These approximations often introduce a mismatch between the learner's objective and the desired application performance, leading to inconsistency. We take a different approach: adversarially approximate training data while optimizing the exact F-score or AER. Structured predictions under this formulation result from solving zero-sum games between a predictor seeking the best performance and an adversary seeking the worst while required to (approximately) match certain structured properties of the training data. We explore this approach for word alignment (AER evaluation) and named entity recognition (F-score evaluation) with linear-chain constraints.

ADA: A Game-Theoretic Perspective on Data Augmentation for Object Detection

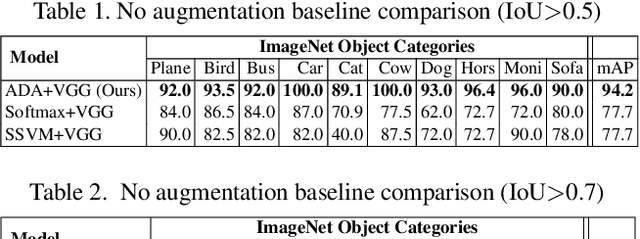
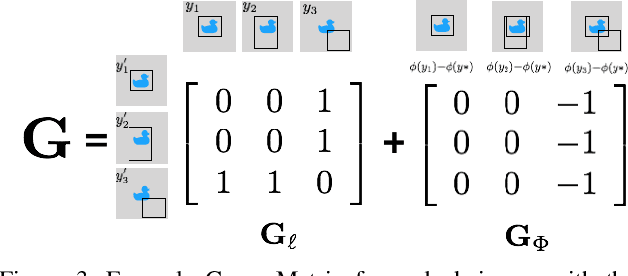
The use of random perturbations of ground truth data, such as random translation or scaling of bounding boxes, is a common heuristic used for data augmentation that has been shown to prevent overfitting and improve generalization. Since the design of data augmentation is largely guided by reported best practices, it is difficult to understand if those design choices are optimal. To provide a more principled perspective, we develop a game-theoretic interpretation of data augmentation in the context of object detection. We aim to find an optimal adversarial perturbations of the ground truth data (i.e., the worst case perturbations) that forces the object bounding box predictor to learn from the hardest distribution of perturbed examples for better test-time performance. We establish that the game theoretic solution, the Nash equilibrium, provides both an optimal predictor and optimal data augmentation distribution. We show that our adversarial method of training a predictor can significantly improve test time performance for the task of object detection. On the ImageNet object detection task, our adversarial approach improves performance by over 16\% compared to the best performing data augmentation method

Computational Rationalization: The Inverse Equilibrium Problem

Modeling the purposeful behavior of imperfect agents from a small number of observations is a challenging task. When restricted to the single-agent decision-theoretic setting, inverse optimal control techniques assume that observed behavior is an approximately optimal solution to an unknown decision problem. These techniques learn a utility function that explains the example behavior and can then be used to accurately predict or imitate future behavior in similar observed or unobserved situations. In this work, we consider similar tasks in competitive and cooperative multi-agent domains. Here, unlike single-agent settings, a player cannot myopically maximize its reward; it must speculate on how the other agents may act to influence the game's outcome. Employing the game-theoretic notion of regret and the principle of maximum entropy, we introduce a technique for predicting and generalizing behavior.

Learning Selectively Conditioned Forest Structures with Applications to DBNs and Classification

Dealing with uncertainty in Bayesian Network structures using maximum a posteriori (MAP) estimation or Bayesian Model Averaging (BMA) is often intractable due to the superexponential number of possible directed, acyclic graphs. When the prior is decomposable, two classes of graphs where efficient learning can take place are tree structures, and fixed-orderings with limited in-degree. We show how MAP estimates and BMA for selectively conditioned forests (SCF), a combination of these two classes, can be computed efficiently for ordered sets of variables. We apply SCFs to temporal data to learn Dynamic Bayesian Networks having an intra-timestep forest and inter-timestep limited in-degree structure, improving model accuracy over DBNs without the combination of structures. We also apply SCFs to Bayes Net classification to learn selective forest augmented Naive Bayes classifiers. We argue that the built-in feature selection of selective augmented Bayes classifiers makes them preferable to similar non-selective classifiers based on empirical evidence.