Partitioning Message Passing for Graph Fraud Detection

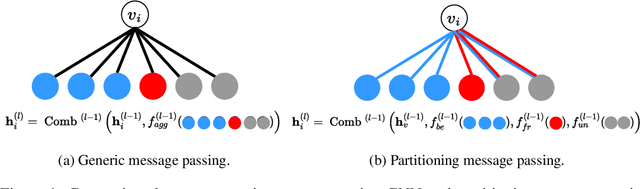
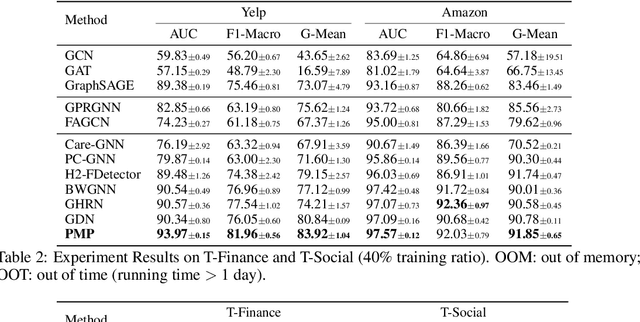
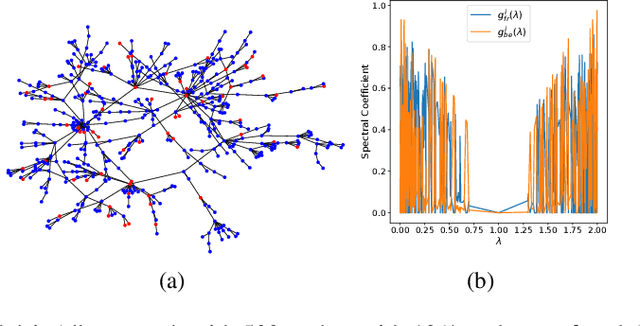
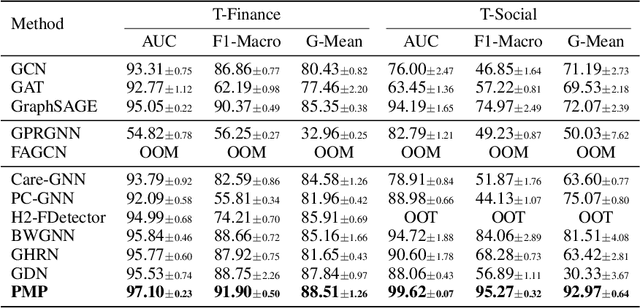
Label imbalance and homophily-heterophily mixture are the fundamental problems encountered when applying Graph Neural Networks (GNNs) to Graph Fraud Detection (GFD) tasks. Existing GNN-based GFD models are designed to augment graph structure to accommodate the inductive bias of GNNs towards homophily, by excluding heterophilic neighbors during message passing. In our work, we argue that the key to applying GNNs for GFD is not to exclude but to {\em distinguish} neighbors with different labels. Grounded in this perspective, we introduce Partitioning Message Passing (PMP), an intuitive yet effective message passing paradigm expressly crafted for GFD. Specifically, in the neighbor aggregation stage of PMP, neighbors with different classes are aggregated with distinct node-specific aggregation functions. By this means, the center node can adaptively adjust the information aggregated from its heterophilic and homophilic neighbors, thus avoiding the model gradient being dominated by benign nodes which occupy the majority of the population. We theoretically establish a connection between the spatial formulation of PMP and spectral analysis to characterize that PMP operates an adaptive node-specific spectral graph filter, which demonstrates the capability of PMP to handle heterophily-homophily mixed graphs. Extensive experimental results show that PMP can significantly boost the performance on GFD tasks.

Fairness for Robust Learning to Rank

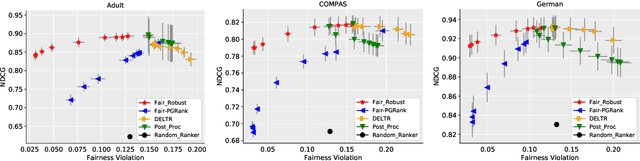
While conventional ranking systems focus solely on maximizing the utility of the ranked items to users, fairness-aware ranking systems additionally try to balance the exposure for different protected attributes such as gender or race. To achieve this type of group fairness for ranking, we derive a new ranking system based on the first principles of distributional robustness. We formulate a minimax game between a player choosing a distribution over rankings to maximize utility while satisfying fairness constraints against an adversary seeking to minimize utility while matching statistics of the training data. We show that our approach provides better utility for highly fair rankings than existing baseline methods.

AP-Perf: Incorporating Generic Performance Metrics in Differentiable Learning

We propose a method that enables practitioners to conveniently incorporate custom non-decomposable performance metrics into differentiable learning pipelines, notably those based upon deep learning architectures. Our approach is based on the recently-developed adversarial prediction framework, a distributionally robust approach that optimizes a metric in the worst case given the statistical summary of the empirical distribution. We formulate a marginal distribution technique to reduce the complexity of optimizing the adversarial prediction formulation over a vast range of non-decomposable metrics. We demonstrate how easy it is to write and incorporate complex custom metrics using our provided tool. Finally, we show the effectiveness of our approach for image classification tasks using MNIST and Fashion-MNIST datasets as well as classification task on tabular data using UCI repository and benchmark datasets.

Fair Logistic Regression: An Adversarial Perspective

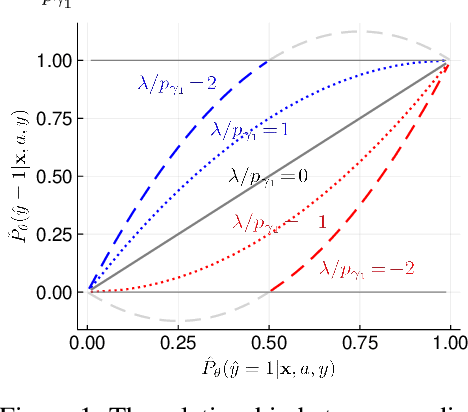
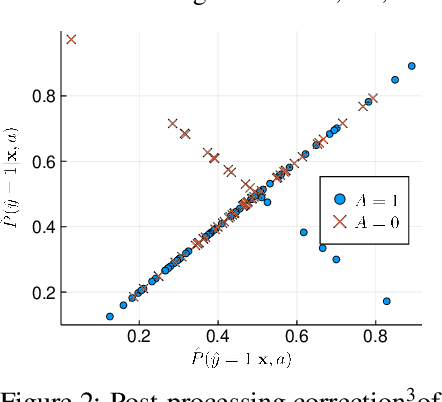
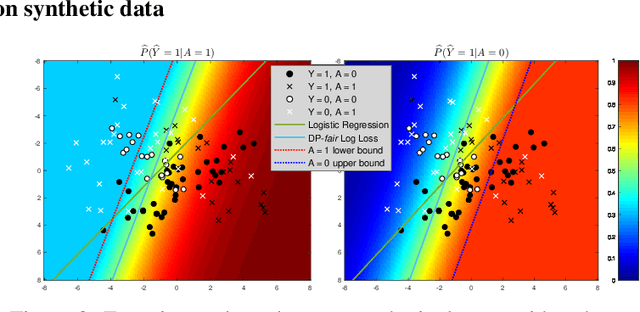
Fair prediction methods have primarily been built around existing classification techniques using pre-processing methods, post-hoc adjustments, reduction-based constructions, or deep learning procedures. We investigate a new approach to fair data-driven decision making by designing predictors with fairness requirements integrated into their core formulations. We augment a game-theoretic construction of the logistic regression model with fairness constraints, producing a novel prediction model that robustly and fairly minimizes the logarithmic loss. We demonstrate the advantages of our approach on a range of benchmark datasets for fairness.

Consistent Robust Adversarial Prediction for General Multiclass Classification

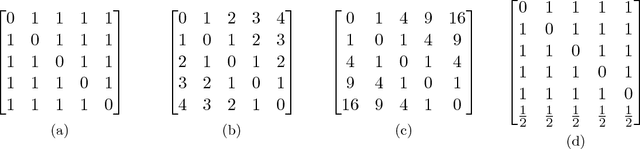
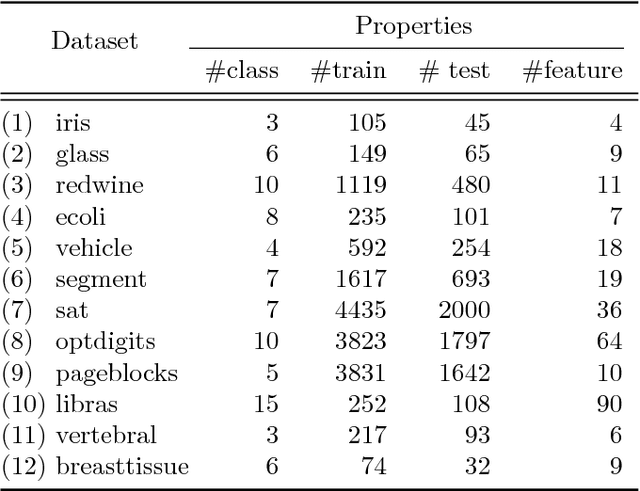
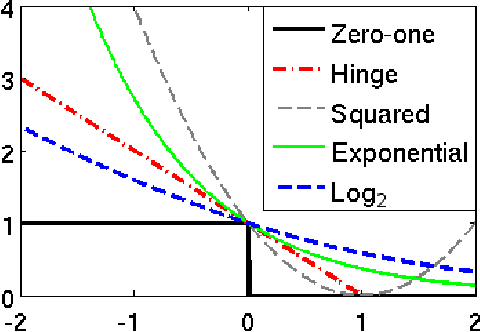
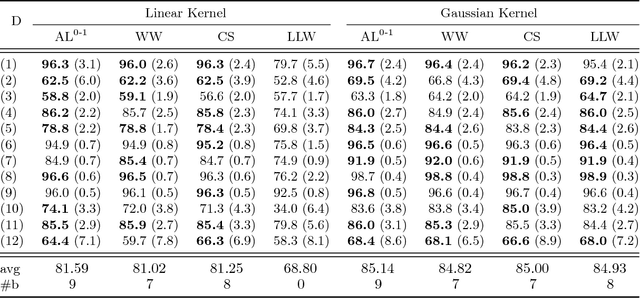
We propose a robust adversarial prediction framework for general multiclass classification. Our method seeks predictive distributions that robustly optimize non-convex and non-continuous multiclass loss metrics against the worst-case conditional label distributions (the adversarial distributions) that (approximately) match the statistics of the training data. Although the optimized loss metrics are non-convex and non-continuous, the dual formulation of the framework is a convex optimization problem that can be recast as a risk minimization model with a prescribed convex surrogate loss we call the adversarial surrogate loss. We show that the adversarial surrogate losses fill an existing gap in surrogate loss construction for general multiclass classification problems, by simultaneously aligning better with the original multiclass loss, guaranteeing Fisher consistency, enabling a way to incorporate rich feature spaces via the kernel trick, and providing competitive performance in practice.

Distributionally Robust Graphical Models

In many structured prediction problems, complex relationships between variables are compactly defined using graphical structures. The most prevalent graphical prediction methods---probabilistic graphical models and large margin methods---have their own distinct strengths but also possess significant drawbacks. Conditional random fields (CRFs) are Fisher consistent, but they do not permit integration of customized loss metrics into their learning process. Large-margin models, such as structured support vector machines (SSVMs), have the flexibility to incorporate customized loss metrics, but lack Fisher consistency guarantees. We present adversarial graphical models (AGM), a distributionally robust approach for constructing a predictor that performs robustly for a class of data distributions defined using a graphical structure. Our approach enjoys both the flexibility of incorporating customized loss metrics into its design as well as the statistical guarantee of Fisher consistency. We present exact learning and prediction algorithms for AGM with time complexity similar to existing graphical models and show the practical benefits of our approach with experiments.

Kernel Robust Bias-Aware Prediction under Covariate Shift

Under covariate shift, training (source) data and testing (target) data differ in input space distribution, but share the same conditional label distribution. This poses a challenging machine learning task. Robust Bias-Aware (RBA) prediction provides the conditional label distribution that is robust to the worstcase logarithmic loss for the target distribution while matching feature expectation constraints from the source distribution. However, employing RBA with insufficient feature constraints may result in high certainty predictions for much of the source data, while leaving too much uncertainty for target data predictions. To overcome this issue, we extend the representer theorem to the RBA setting, enabling minimization of regularized expected target risk by a reweighted kernel expectation under the source distribution. By applying kernel methods, we establish consistency guarantees and demonstrate better performance of the RBA classifier than competing methods on synthetically biased UCI datasets as well as datasets that have natural covariate shift.