Fairness for Robust Learning to Rank

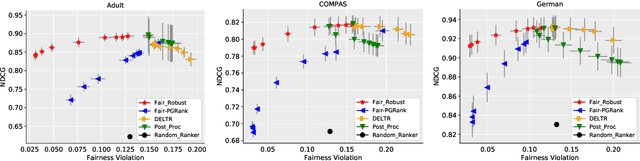
While conventional ranking systems focus solely on maximizing the utility of the ranked items to users, fairness-aware ranking systems additionally try to balance the exposure for different protected attributes such as gender or race. To achieve this type of group fairness for ranking, we derive a new ranking system based on the first principles of distributional robustness. We formulate a minimax game between a player choosing a distribution over rankings to maximize utility while satisfying fairness constraints against an adversary seeking to minimize utility while matching statistics of the training data. We show that our approach provides better utility for highly fair rankings than existing baseline methods.

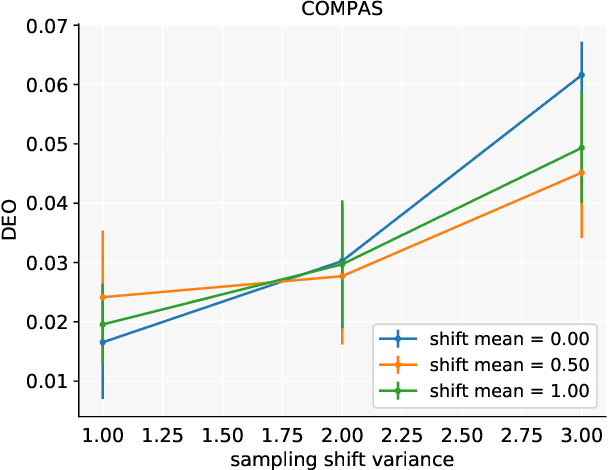
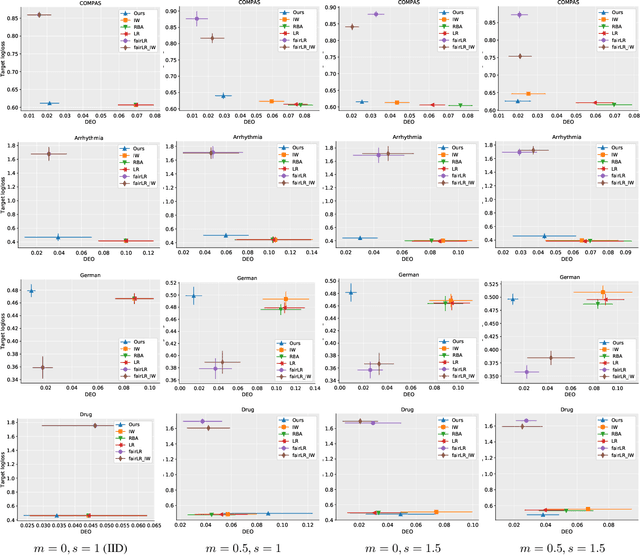
Robust Fairness under Covariate Shift

Making predictions that are fair with regard to protected group membership (race, gender, age, etc.) has become an important requirement for classification algorithms. Existing techniques derive a fair model from sampled labeled data relying on the assumption that training and testing data are identically and independently drawn (iid) from the same distribution.In practice, distribution shift can and does occur between training and testing datasets as the characteristics of individuals interacting with the machine learning system -- and which individuals interact with the system -- change. We investigate fairness under covariate shift, a relaxation of the iid assumption in which the inputs or covariates change while the conditional label distribution remains the same. We seek fair decisions under these assumptions on target data with unknown labels.We propose an approach that obtains the predictor that is robust to the worst-case in terms of target performance while satisfying target fairness requirements and matching statistical properties of the source data. We demonstrate the benefits of our approach on benchmark prediction tasks.

Fair Logistic Regression: An Adversarial Perspective

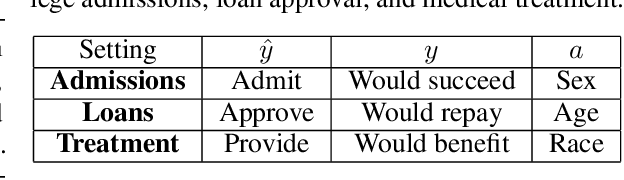
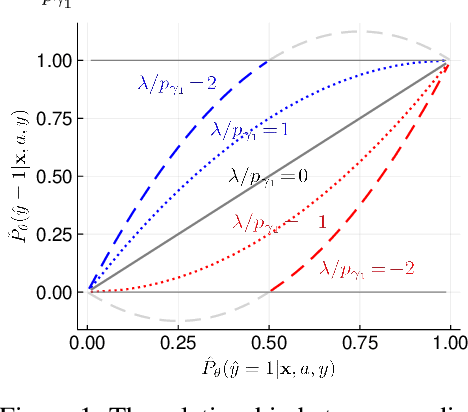
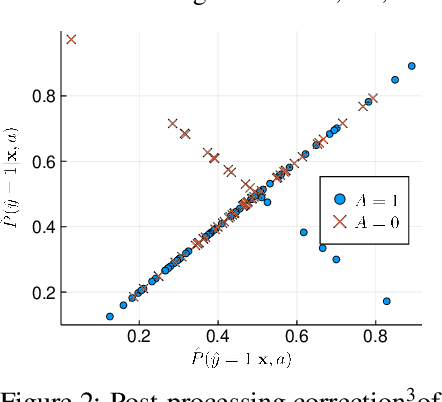
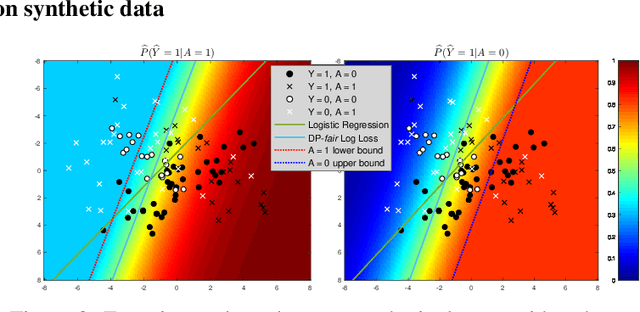
Fair prediction methods have primarily been built around existing classification techniques using pre-processing methods, post-hoc adjustments, reduction-based constructions, or deep learning procedures. We investigate a new approach to fair data-driven decision making by designing predictors with fairness requirements integrated into their core formulations. We augment a game-theoretic construction of the logistic regression model with fairness constraints, producing a novel prediction model that robustly and fairly minimizes the logarithmic loss. We demonstrate the advantages of our approach on a range of benchmark datasets for fairness.

Distributionally Robust Graphical Models

In many structured prediction problems, complex relationships between variables are compactly defined using graphical structures. The most prevalent graphical prediction methods---probabilistic graphical models and large margin methods---have their own distinct strengths but also possess significant drawbacks. Conditional random fields (CRFs) are Fisher consistent, but they do not permit integration of customized loss metrics into their learning process. Large-margin models, such as structured support vector machines (SSVMs), have the flexibility to incorporate customized loss metrics, but lack Fisher consistency guarantees. We present adversarial graphical models (AGM), a distributionally robust approach for constructing a predictor that performs robustly for a class of data distributions defined using a graphical structure. Our approach enjoys both the flexibility of incorporating customized loss metrics into its design as well as the statistical guarantee of Fisher consistency. We present exact learning and prediction algorithms for AGM with time complexity similar to existing graphical models and show the practical benefits of our approach with experiments.

Adversarial Structured Prediction for Multivariate Measures

Many predicted structured objects (e.g., sequences, matchings, trees) are evaluated using the F-score, alignment error rate (AER), or other multivariate performance measures. Since inductively optimizing these measures using training data is typically computationally difficult, empirical risk minimization of surrogate losses is employed, using, e.g., the hinge loss for (structured) support vector machines. These approximations often introduce a mismatch between the learner's objective and the desired application performance, leading to inconsistency. We take a different approach: adversarially approximate training data while optimizing the exact F-score or AER. Structured predictions under this formulation result from solving zero-sum games between a predictor seeking the best performance and an adversary seeking the worst while required to (approximately) match certain structured properties of the training data. We explore this approach for word alignment (AER evaluation) and named entity recognition (F-score evaluation) with linear-chain constraints.