Mohammad Ali Bashiri
Consistent Robust Adversarial Prediction for General Multiclass Classification
Dec 18, 2018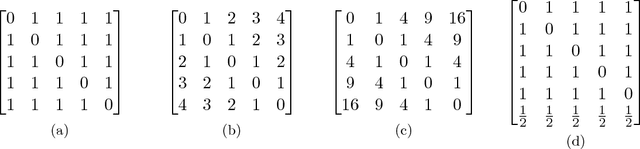
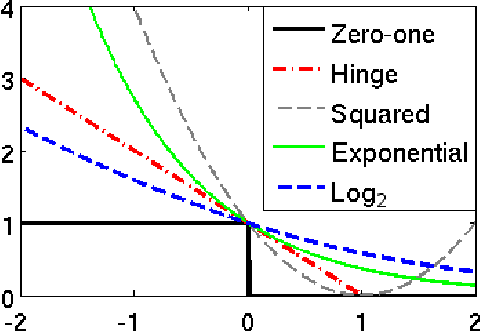
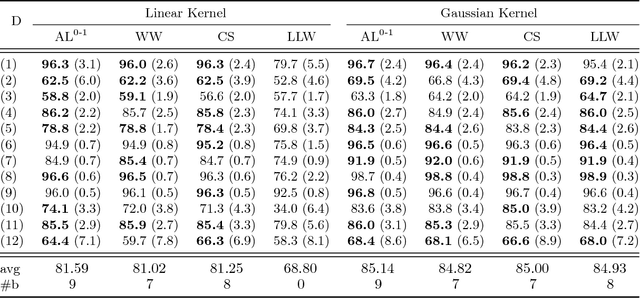
Abstract:We propose a robust adversarial prediction framework for general multiclass classification. Our method seeks predictive distributions that robustly optimize non-convex and non-continuous multiclass loss metrics against the worst-case conditional label distributions (the adversarial distributions) that (approximately) match the statistics of the training data. Although the optimized loss metrics are non-convex and non-continuous, the dual formulation of the framework is a convex optimization problem that can be recast as a risk minimization model with a prescribed convex surrogate loss we call the adversarial surrogate loss. We show that the adversarial surrogate losses fill an existing gap in surrogate loss construction for general multiclass classification problems, by simultaneously aligning better with the original multiclass loss, guaranteeing Fisher consistency, enabling a way to incorporate rich feature spaces via the kernel trick, and providing competitive performance in practice.
Distributionally Robust Graphical Models
Nov 07, 2018



Abstract:In many structured prediction problems, complex relationships between variables are compactly defined using graphical structures. The most prevalent graphical prediction methods---probabilistic graphical models and large margin methods---have their own distinct strengths but also possess significant drawbacks. Conditional random fields (CRFs) are Fisher consistent, but they do not permit integration of customized loss metrics into their learning process. Large-margin models, such as structured support vector machines (SSVMs), have the flexibility to incorporate customized loss metrics, but lack Fisher consistency guarantees. We present adversarial graphical models (AGM), a distributionally robust approach for constructing a predictor that performs robustly for a class of data distributions defined using a graphical structure. Our approach enjoys both the flexibility of incorporating customized loss metrics into its design as well as the statistical guarantee of Fisher consistency. We present exact learning and prediction algorithms for AGM with time complexity similar to existing graphical models and show the practical benefits of our approach with experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge