Robust Covariate Shift Prediction with General Losses and Feature Views
Paper and Code
Dec 28, 2017
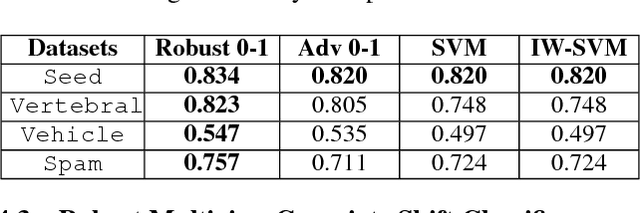

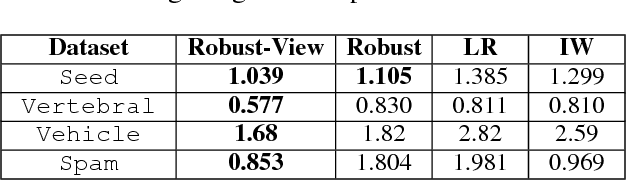
Covariate shift relaxes the widely-employed independent and identically distributed (IID) assumption by allowing different training and testing input distributions. Unfortunately, common methods for addressing covariate shift by trying to remove the bias between training and testing distributions using importance weighting often provide poor performance guarantees in theory and unreliable predictions with high variance in practice. Recently developed methods that construct a predictor that is inherently robust to the difficulties of learning under covariate shift are restricted to minimizing logloss and can be too conservative when faced with high-dimensional learning tasks. We address these limitations in two ways: by robustly minimizing various loss functions, including non-convex ones, under the testing distribution; and by separately shaping the influence of covariate shift according to different feature-based views of the relationship between input variables and example labels. These generalizations make robust covariate shift prediction applicable to more task scenarios. We demonstrate the benefits on classification under covariate shift tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge