Player of Games

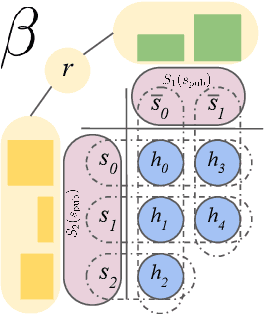
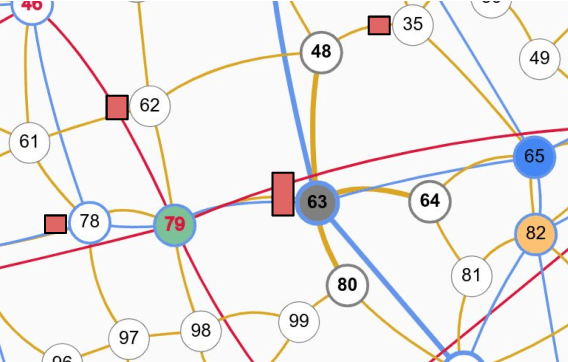
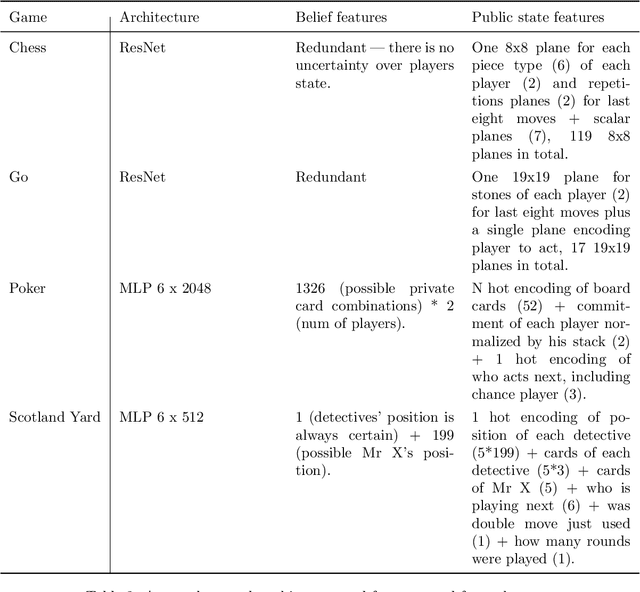
Games have a long history of serving as a benchmark for progress in artificial intelligence. Recently, approaches using search and learning have shown strong performance across a set of perfect information games, and approaches using game-theoretic reasoning and learning have shown strong performance for specific imperfect information poker variants. We introduce Player of Games, a general-purpose algorithm that unifies previous approaches, combining guided search, self-play learning, and game-theoretic reasoning. Player of Games is the first algorithm to achieve strong empirical performance in large perfect and imperfect information games -- an important step towards truly general algorithms for arbitrary environments. We prove that Player of Games is sound, converging to perfect play as available computation time and approximation capacity increases. Player of Games reaches strong performance in chess and Go, beats the strongest openly available agent in heads-up no-limit Texas hold'em poker (Slumbot), and defeats the state-of-the-art agent in Scotland Yard, an imperfect information game that illustrates the value of guided search, learning, and game-theoretic reasoning.

Variance Reduction in Monte Carlo Counterfactual Regret Minimization (VR-MCCFR) for Extensive Form Games using Baselines

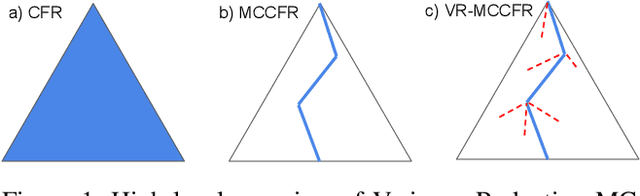
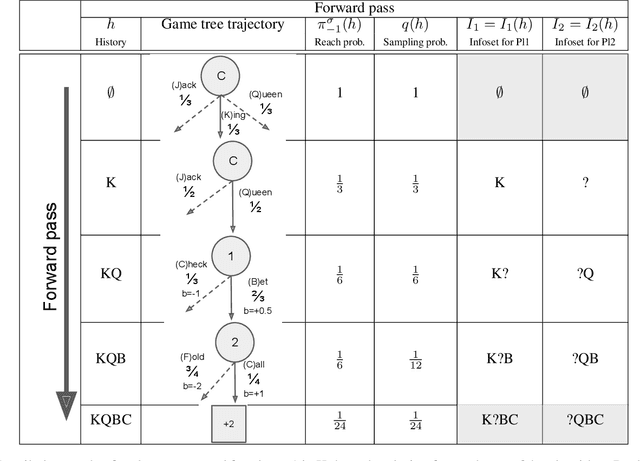
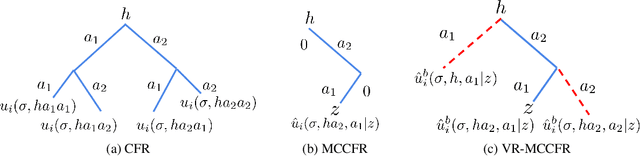
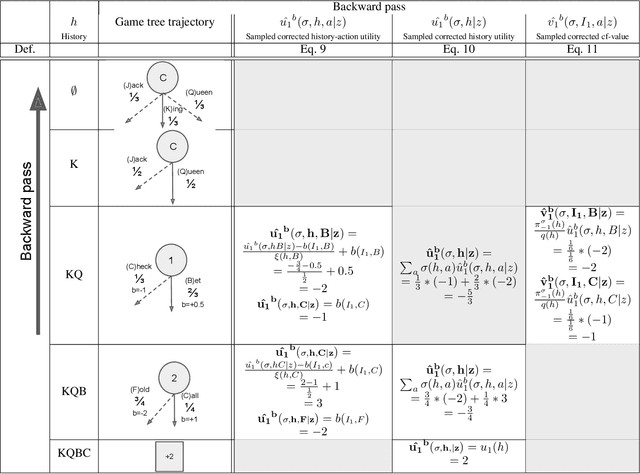
Learning strategies for imperfect information games from samples of interaction is a challenging problem. A common method for this setting, Monte Carlo Counterfactual Regret Minimization (MCCFR), can have slow long-term convergence rates due to high variance. In this paper, we introduce a variance reduction technique (VR-MCCFR) that applies to any sampling variant of MCCFR. Using this technique, per-iteration estimated values and updates are reformulated as a function of sampled values and state-action baselines, similar to their use in policy gradient reinforcement learning. The new formulation allows estimates to be bootstrapped from other estimates within the same episode, propagating the benefits of baselines along the sampled trajectory; the estimates remain unbiased even when bootstrapping from other estimates. Finally, we show that given a perfect baseline, the variance of the value estimates can be reduced to zero. Experimental evaluation shows that VR-MCCFR brings an order of magnitude speedup, while the empirical variance decreases by three orders of magnitude. The decreased variance allows for the first time CFR+ to be used with sampling, increasing the speedup to two orders of magnitude.