Empirical Privacy Variance

We propose the notion of empirical privacy variance and study it in the context of differentially private fine-tuning of language models. Specifically, we show that models calibrated to the same $(\varepsilon, \delta)$-DP guarantee using DP-SGD with different hyperparameter configurations can exhibit significant variations in empirical privacy, which we quantify through the lens of memorization. We investigate the generality of this phenomenon across multiple dimensions and discuss why it is surprising and relevant. Through regression analysis, we examine how individual and composite hyperparameters influence empirical privacy. The results reveal a no-free-lunch trade-off: existing practices of hyperparameter tuning in DP-SGD, which focus on optimizing utility under a fixed privacy budget, often come at the expense of empirical privacy. To address this, we propose refined heuristics for hyperparameter selection that explicitly account for empirical privacy, showing that they are both precise and practically useful. Finally, we take preliminary steps to understand empirical privacy variance. We propose two hypotheses, identify limitations in existing techniques like privacy auditing, and outline open questions for future research.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Optimal Group Fair Classifiers from Linear Post-Processing

We propose a post-processing algorithm for fair classification that mitigates model bias under a unified family of group fairness criteria covering statistical parity, equal opportunity, and equalized odds, applicable to multi-class problems and both attribute-aware and attribute-blind settings. It achieves fairness by re-calibrating the output score of the given base model with a "fairness cost" -- a linear combination of the (predicted) group memberships. Our algorithm is based on a representation result showing that the optimal fair classifier can be expressed as a linear post-processing of the loss function and the group predictor, derived via using these as sufficient statistics to reformulate the fair classification problem as a linear program. The parameters of the post-processor are estimated by solving the empirical LP. Experiments on benchmark datasets show the efficiency and effectiveness of our algorithm at reducing disparity compared to existing algorithms, including in-processing, especially on larger problems.

Differentially Private Post-Processing for Fair Regression

This paper describes a differentially private post-processing algorithm for learning fair regressors satisfying statistical parity, addressing privacy concerns of machine learning models trained on sensitive data, as well as fairness concerns of their potential to propagate historical biases. Our algorithm can be applied to post-process any given regressor to improve fairness by remapping its outputs. It consists of three steps: first, the output distributions are estimated privately via histogram density estimation and the Laplace mechanism, then their Wasserstein barycenter is computed, and the optimal transports to the barycenter are used for post-processing to satisfy fairness. We analyze the sample complexity of our algorithm and provide fairness guarantee, revealing a trade-off between the statistical bias and variance induced from the choice of the number of bins in the histogram, in which using less bins always favors fairness at the expense of error.

Revisiting Scalarization in Multi-Task Learning: A Theoretical Perspective

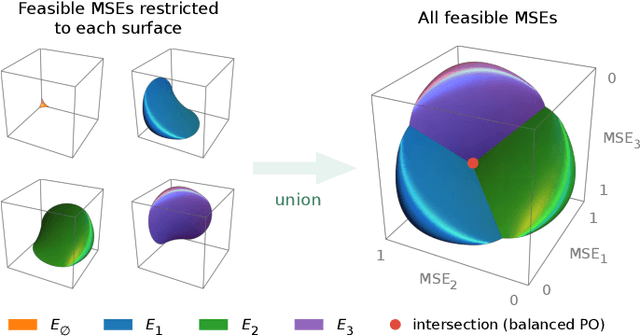
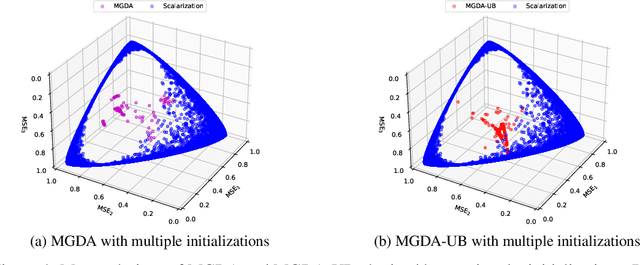
Linear scalarization, i.e., combining all loss functions by a weighted sum, has been the default choice in the literature of multi-task learning (MTL) since its inception. In recent years, there is a surge of interest in developing Specialized Multi-Task Optimizers (SMTOs) that treat MTL as a multi-objective optimization problem. However, it remains open whether there is a fundamental advantage of SMTOs over scalarization. In fact, heated debates exist in the community comparing these two types of algorithms, mostly from an empirical perspective. To approach the above question, in this paper, we revisit scalarization from a theoretical perspective. We focus on linear MTL models and study whether scalarization is capable of fully exploring the Pareto front. Our findings reveal that, in contrast to recent works that claimed empirical advantages of scalarization, scalarization is inherently incapable of full exploration, especially for those Pareto optimal solutions that strike the balanced trade-offs between multiple tasks. More concretely, when the model is under-parametrized, we reveal a multi-surface structure of the feasible region and identify necessary and sufficient conditions for full exploration. This leads to the conclusion that scalarization is in general incapable of tracing out the Pareto front. Our theoretical results partially answer the open questions in Xin et al. (2021), and provide a more intuitive explanation on why scalarization fails beyond non-convexity. We additionally perform experiments on a real-world dataset using both scalarization and state-of-the-art SMTOs. The experimental results not only corroborate our theoretical findings, but also unveil the potential of SMTOs in finding balanced solutions, which cannot be achieved by scalarization.

Learning List-Level Domain-Invariant Representations for Ranking

Domain adaptation aims to transfer the knowledge acquired by models trained on (data-rich) source domains to (low-resource) target domains, for which a popular method is invariant representation learning. While they have been studied extensively for classification and regression problems, how they apply to ranking problems, where the data and metrics have a list structure, is not well understood. Theoretically, we establish a domain adaptation generalization bound for ranking under listwise metrics such as MRR and NDCG. The bound suggests an adaptation method via learning list-level domain-invariant feature representations, whose benefits are empirically demonstrated by unsupervised domain adaptation experiments on real-world ranking tasks, including passage reranking. A key message is that for domain adaptation, the representations should be analyzed at the same level at which the metric is computed, as we show that learning invariant representations at the list level is most effective for adaptation on ranking problems.

Fair and Optimal Classification via Transports to Wasserstein-Barycenter

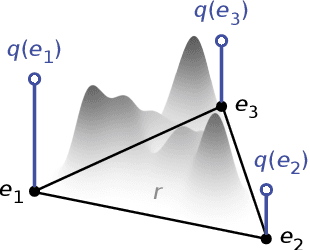
Fairness in automated decision-making systems has gained increasing attention as their applications expand to real-world high-stakes domains. To facilitate the design of fair ML systems, it is essential to understand the potential trade-offs between fairness and predictive power, and the construction of the optimal predictor under a given fairness constraint. In this paper, for general classification problems under the group fairness criterion of demographic parity (DP), we precisely characterize the trade-off between DP and classification accuracy, referred to as the minimum cost of fairness. Our insight comes from the key observation that finding the optimal fair classifier is equivalent to solving a Wasserstein-barycenter problem under $\ell_1$-norm restricted to the vertices of the probability simplex. Inspired by our characterization, we provide a construction of an optimal fair classifier achieving this minimum cost via the composition of the Bayes regressor and optimal transports from its output distributions to the barycenter. Our construction naturally leads to an algorithm for post-processing any pre-trained predictor to satisfy DP fairness, complemented with finite sample guarantees. Experiments on real-world datasets verify and demonstrate the effectiveness of our approaches.

Neural tangent kernels, transportation mappings, and universal approximation

This paper establishes rates of universal approximation for the shallow neural tangent kernel (NTK): network weights are only allowed microscopic changes from random initialization, which entails that activations are mostly unchanged, and the network is nearly equivalent to its linearization. Concretely, the paper has two main contributions: a generic scheme to approximate functions with the NTK by sampling from transport mappings between the initial weights and their desired values, and the construction of transport mappings via Fourier transforms. Regarding the first contribution, the proof scheme provides another perspective on how the NTK regime arises from rescaling: redundancy in the weights due to resampling allows individual weights to be scaled down. Regarding the second contribution, the most notable transport mapping asserts that roughly $1 / \delta^{10d}$ nodes are sufficient to approximate continuous functions, where $\delta$ depends on the continuity properties of the target function. By contrast, nearly the same proof yields a bound of $1 / \delta^{2d}$ for shallow ReLU networks; this gap suggests a tantalizing direction for future work, separating shallow ReLU networks and their linearization.

Approximation power of random neural networks

This paper investigates the approximation power of three types of random neural networks: (a) infinite width networks, with weights following an arbitrary distribution; (b) finite width networks obtained by subsampling the preceding infinite width networks; (c) finite width networks obtained by starting with standard Gaussian initialization, and then adding a vanishingly small correction to the weights. The primary result is a fully quantified bound on the rate of approximation of general general continuous functions: in all three cases, a function $f$ can be approximated with complexity $\|f\|_1 (d/\delta)^{\mathcal{O}(d)}$, where $\delta$ depends on continuity properties of $f$ and the complexity measure depends on the weight magnitudes and/or cardinalities. Along the way, a variety of ancillary results are developed: an exact construction of Gaussian densities with infinite width networks, an elementary stand-alone proof scheme for approximation via convolutions of radial basis functions, subsampling rates for infinite width networks, and depth separation for corrected networks.