Lang Yin
Data Shifts Hurt CoT: A Theoretical Study
Jun 12, 2025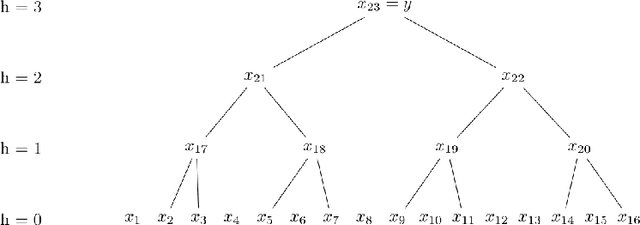
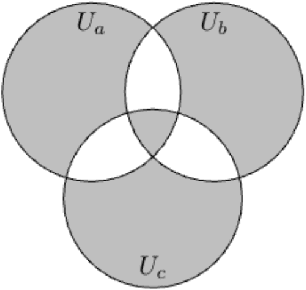
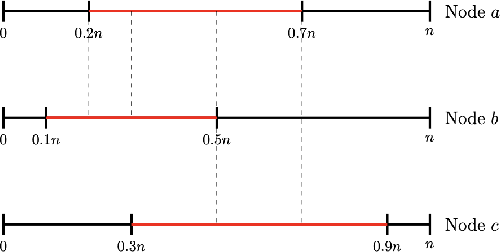
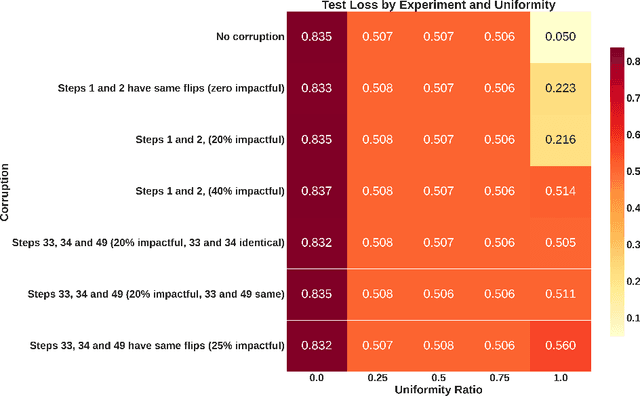
Abstract:Chain of Thought (CoT) has been applied to various large language models (LLMs) and proven to be effective in improving the quality of outputs. In recent studies, transformers are proven to have absolute upper bounds in terms of expressive power, and consequently, they cannot solve many computationally difficult problems. However, empowered by CoT, transformers are proven to be able to solve some difficult problems effectively, such as the $k$-parity problem. Nevertheless, those works rely on two imperative assumptions: (1) identical training and testing distribution, and (2) corruption-free training data with correct reasoning steps. However, in the real world, these assumptions do not always hold. Although the risks of data shifts have caught attention, our work is the first to rigorously study the exact harm caused by such shifts to the best of our knowledge. Focusing on the $k$-parity problem, in this work we investigate the joint impact of two types of data shifts: the distribution shifts and data poisoning, on the quality of trained models obtained by a well-established CoT decomposition. In addition to revealing a surprising phenomenon that CoT leads to worse performance on learning parity than directly generating the prediction, our technical results also give a rigorous and comprehensive explanation of the mechanistic reasons of such impact.
On the Expressive Power of Tree-Structured Probabilistic Circuits
Oct 07, 2024Abstract:Probabilistic circuits (PCs) have emerged as a powerful framework to compactly represent probability distributions for efficient and exact probabilistic inference. It has been shown that PCs with a general directed acyclic graph (DAG) structure can be understood as a mixture of exponentially (in its height) many components, each of which is a product distribution over univariate marginals. However, existing structure learning algorithms for PCs often generate tree-structured circuits or use tree-structured circuits as intermediate steps to compress them into DAG-structured circuits. This leads to the intriguing question of whether there exists an exponential gap between DAGs and trees for the PC structure. In this paper, we provide a negative answer to this conjecture by proving that, for $n$ variables, there exists a sub-exponential upper bound $n^{O(\log n)}$ on the size of an equivalent tree computing the same probability distribution. On the other hand, we also show that given a depth restriction on the tree, there is a super-polynomial separation between tree and DAG-structured PCs. Our work takes an important step towards understanding the expressive power of tree-structured PCs, and our techniques may be of independent interest in the study of structure learning algorithms for PCs.
Revisiting Scalarization in Multi-Task Learning: A Theoretical Perspective
Aug 27, 2023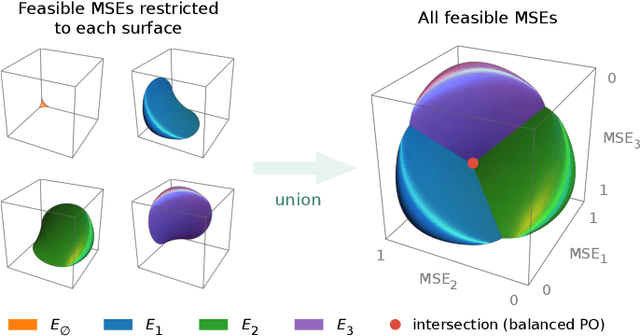

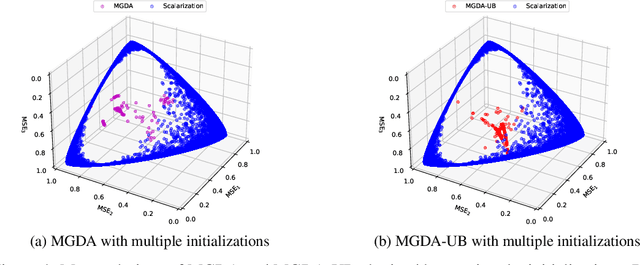

Abstract:Linear scalarization, i.e., combining all loss functions by a weighted sum, has been the default choice in the literature of multi-task learning (MTL) since its inception. In recent years, there is a surge of interest in developing Specialized Multi-Task Optimizers (SMTOs) that treat MTL as a multi-objective optimization problem. However, it remains open whether there is a fundamental advantage of SMTOs over scalarization. In fact, heated debates exist in the community comparing these two types of algorithms, mostly from an empirical perspective. To approach the above question, in this paper, we revisit scalarization from a theoretical perspective. We focus on linear MTL models and study whether scalarization is capable of fully exploring the Pareto front. Our findings reveal that, in contrast to recent works that claimed empirical advantages of scalarization, scalarization is inherently incapable of full exploration, especially for those Pareto optimal solutions that strike the balanced trade-offs between multiple tasks. More concretely, when the model is under-parametrized, we reveal a multi-surface structure of the feasible region and identify necessary and sufficient conditions for full exploration. This leads to the conclusion that scalarization is in general incapable of tracing out the Pareto front. Our theoretical results partially answer the open questions in Xin et al. (2021), and provide a more intuitive explanation on why scalarization fails beyond non-convexity. We additionally perform experiments on a real-world dataset using both scalarization and state-of-the-art SMTOs. The experimental results not only corroborate our theoretical findings, but also unveil the potential of SMTOs in finding balanced solutions, which cannot be achieved by scalarization.
Fair and Optimal Classification via Transports to Wasserstein-Barycenter
Nov 03, 2022
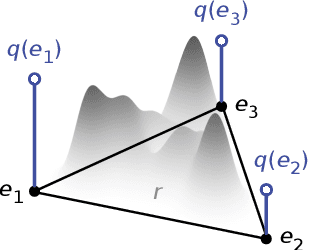


Abstract:Fairness in automated decision-making systems has gained increasing attention as their applications expand to real-world high-stakes domains. To facilitate the design of fair ML systems, it is essential to understand the potential trade-offs between fairness and predictive power, and the construction of the optimal predictor under a given fairness constraint. In this paper, for general classification problems under the group fairness criterion of demographic parity (DP), we precisely characterize the trade-off between DP and classification accuracy, referred to as the minimum cost of fairness. Our insight comes from the key observation that finding the optimal fair classifier is equivalent to solving a Wasserstein-barycenter problem under $\ell_1$-norm restricted to the vertices of the probability simplex. Inspired by our characterization, we provide a construction of an optimal fair classifier achieving this minimum cost via the composition of the Bayes regressor and optimal transports from its output distributions to the barycenter. Our construction naturally leads to an algorithm for post-processing any pre-trained predictor to satisfy DP fairness, complemented with finite sample guarantees. Experiments on real-world datasets verify and demonstrate the effectiveness of our approaches.
FOCUS: Fairness via Agent-Awareness for Federated Learning on Heterogeneous Data
Jul 21, 2022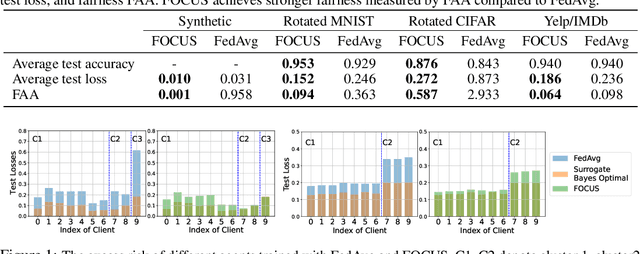

Abstract:Federated learning (FL) provides an effective paradigm to train machine learning models over distributed data with privacy protection. However, recent studies show that FL is subject to various security, privacy, and fairness threats due to the potentially malicious and heterogeneous local agents. For instance, it is vulnerable to local adversarial agents who only contribute low-quality data, with the goal of harming the performance of those with high-quality data. This kind of attack hence breaks existing definitions of fairness in FL that mainly focus on a certain notion of performance parity. In this work, we aim to address this limitation and propose a formal definition of fairness via agent-awareness for FL (FAA), which takes the heterogeneous data contributions of local agents into account. In addition, we propose a fair FL training algorithm based on agent clustering (FOCUS) to achieve FAA. Theoretically, we prove the convergence and optimality of FOCUS under mild conditions for linear models and general convex loss functions with bounded smoothness. We also prove that FOCUS always achieves higher fairness measured by FAA compared with standard FedAvg protocol under both linear models and general convex loss functions. Empirically, we evaluate FOCUS on four datasets, including synthetic data, images, and texts under different settings, and we show that FOCUS achieves significantly higher fairness based on FAA while maintaining similar or even higher prediction accuracy compared with FedAvg.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge