Loss Attitude Aware Energy Management for Signal Detection

This work considers a Bayesian signal processing problem where increasing the power of the probing signal may cause risks or undesired consequences. We employ a market based approach to solve energy management problems for signal detection while balancing multiple objectives. In particular, the optimal amount of resource consumption is determined so as to maximize a profit-loss based expected utility function. Next, we study the human behavior of resource consumption while taking individuals' behavioral disparity into account. Unlike rational decision makers who consume the amount of resource to maximize the expected utility function, human decision makers act to maximize their subjective utilities. We employ prospect theory to model humans' loss aversion towards a risky event. The amount of resource consumption that maximizes the humans' subjective utility is derived to characterize the actual behavior of humans. It is shown that loss attitudes may lead the human to behave quite differently from a rational decision maker.

Compact Multi-level Sparse Neural Networks with Input Independent Dynamic Rerouting

Deep neural networks (DNNs) have shown to provide superb performance in many real life applications, but their large computation cost and storage requirement have prevented them from being deployed to many edge and internet-of-things (IoT) devices. Sparse deep neural networks, whose majority weight parameters are zeros, can substantially reduce the computation complexity and memory consumption of the models. In real-use scenarios, devices may suffer from large fluctuations of the available computation and memory resources under different environment, and the quality of service (QoS) is difficult to maintain due to the long tail inferences with large latency. Facing the real-life challenges, we propose to train a sparse model that supports multiple sparse levels. That is, a hierarchical structure of weights are satisfied such that the locations and the values of the non-zero parameters of the more-sparse sub-model area subset of the less-sparse sub-model. In this way, one can dynamically select the appropriate sparsity level during inference, while the storage cost is capped by the least sparse sub-model. We have verified our methodologies on a variety of DNN models and tasks, including the ResNet-50, PointNet++, GNMT, and graph attention networks. We obtain sparse sub-models with an average of 13.38% weights and 14.97% FLOPs, while the accuracies are as good as their dense counterparts. More-sparse sub-models with 5.38% weights and 4.47% of FLOPs, which are subsets of the less-sparse ones, can be obtained with only 3.25% relative accuracy loss.

A Unified DNN Weight Compression Framework Using Reweighted Optimization Methods

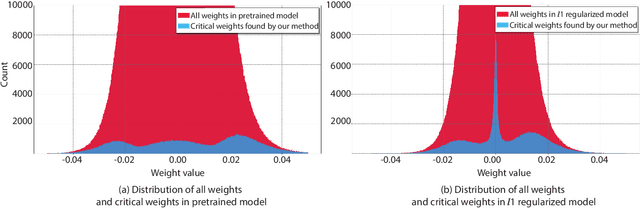
To address the large model size and intensive computation requirement of deep neural networks (DNNs), weight pruning techniques have been proposed and generally fall into two categories, i.e., static regularization-based pruning and dynamic regularization-based pruning. However, the former method currently suffers either complex workloads or accuracy degradation, while the latter one takes a long time to tune the parameters to achieve the desired pruning rate without accuracy loss. In this paper, we propose a unified DNN weight pruning framework with dynamically updated regularization terms bounded by the designated constraint, which can generate both non-structured sparsity and different kinds of structured sparsity. We also extend our method to an integrated framework for the combination of different DNN compression tasks.

Beyond Adversarial Training: Min-Max Optimization in Adversarial Attack and Defense

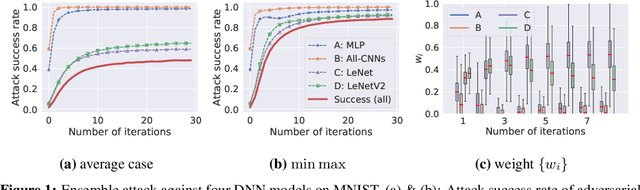
The worst-case training principle that minimizes the maximal adversarial loss, also known as adversarial training (AT), has shown to be a state-of-the-art approach for enhancing adversarial robustness against norm-ball bounded input perturbations. Nonetheless, min-max optimization beyond the purpose of AT has not been rigorously explored in the research of adversarial attack and defense. In particular, given a set of risk sources (domains), minimizing the maximal loss induced from the domain set can be reformulated as a general min-max problem that is different from AT, since the maximization is taken over the probability simplex of the domain set. Examples of this general formulation include attacking model ensembles, devising universal perturbation to input samples or data transformations, and generalized AT over multiple norm-ball threat models. We show that these problems can be solved under a unified and theoretically principled min-max optimization framework. Our proposed approach leads to substantial performance improvement over the uniform averaging strategy in four different tasks. Moreover, we show how the self-adjusted weighting factors of the probability simplex from our proposed algorithms can be used to explain the importance of different attack and defense models.

Progressive DNN Compression: A Key to Achieve Ultra-High Weight Pruning and Quantization Rates using ADMM

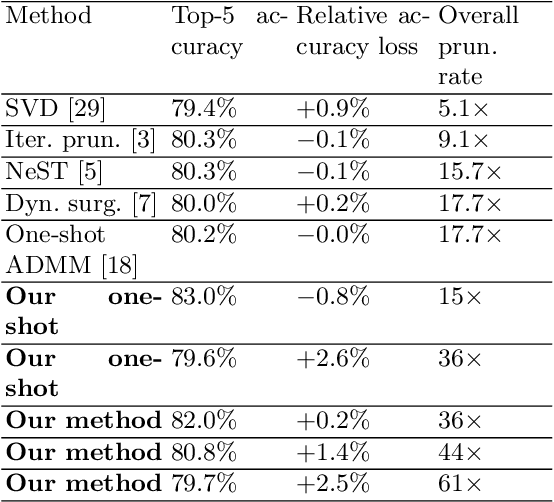
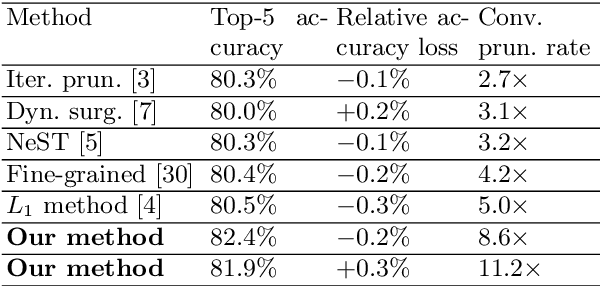
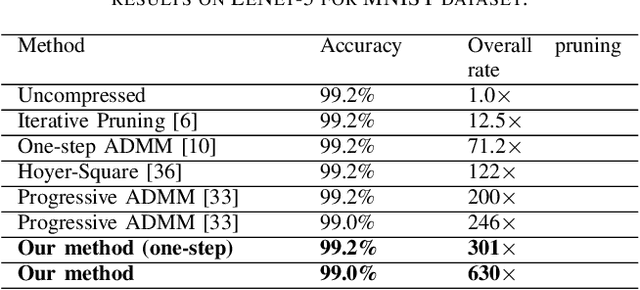
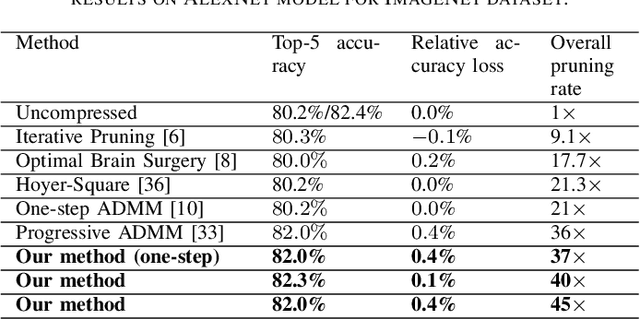
Weight pruning and weight quantization are two important categories of DNN model compression. Prior work on these techniques are mainly based on heuristics. A recent work developed a systematic frame-work of DNN weight pruning using the advanced optimization technique ADMM (Alternating Direction Methods of Multipliers), achieving one of state-of-art in weight pruning results. In this work, we first extend such one-shot ADMM-based framework to guarantee solution feasibility and provide fast convergence rate, and generalize to weight quantization as well. We have further developed a multi-step, progressive DNN weight pruning and quantization framework, with dual benefits of (i) achieving further weight pruning/quantization thanks to the special property of ADMM regularization, and (ii) reducing the search space within each step. Extensive experimental results demonstrate the superior performance compared with prior work. Some highlights: (i) we achieve 246x,36x, and 8x weight pruning on LeNet-5, AlexNet, and ResNet-50 models, respectively, with (almost) zero accuracy loss; (ii) even a significant 61x weight pruning in AlexNet (ImageNet) results in only minor degradation in actual accuracy compared with prior work; (iii) we are among the first to derive notable weight pruning results for ResNet and MobileNet models; (iv) we derive the first lossless, fully binarized (for all layers) LeNet-5 for MNIST and VGG-16 for CIFAR-10; and (v) we derive the first fully binarized (for all layers) ResNet for ImageNet with reasonable accuracy loss.

Progressive Weight Pruning of Deep Neural Networks using ADMM

Deep neural networks (DNNs) although achieving human-level performance in many domains, have very large model size that hinders their broader applications on edge computing devices. Extensive research work have been conducted on DNN model compression or pruning. However, most of the previous work took heuristic approaches. This work proposes a progressive weight pruning approach based on ADMM (Alternating Direction Method of Multipliers), a powerful technique to deal with non-convex optimization problems with potentially combinatorial constraints. Motivated by dynamic programming, the proposed method reaches extremely high pruning rate by using partial prunings with moderate pruning rates. Therefore, it resolves the accuracy degradation and long convergence time problems when pursuing extremely high pruning ratios. It achieves up to 34 times pruning rate for ImageNet dataset and 167 times pruning rate for MNIST dataset, significantly higher than those reached by the literature work. Under the same number of epochs, the proposed method also achieves faster convergence and higher compression rates. The codes and pruned DNN models are released in the link bit.ly/2zxdlss

ADAM-ADMM: A Unified, Systematic Framework of Structured Weight Pruning for DNNs

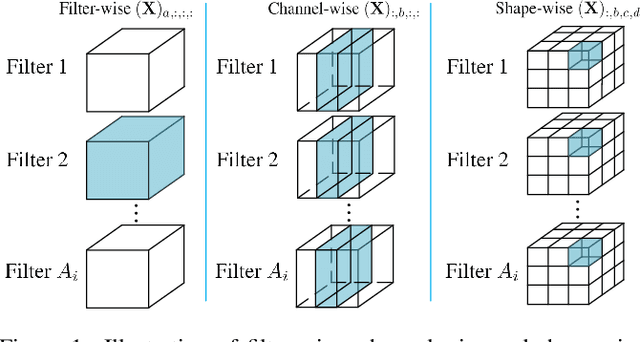
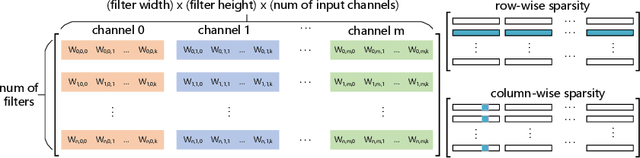
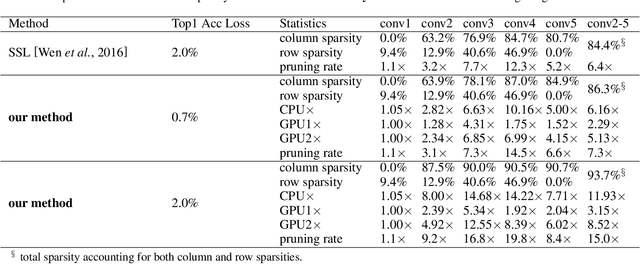
Weight pruning methods of deep neural networks (DNNs) have been demonstrated to achieve a good model pruning ratio without loss of accuracy, thereby alleviating the significant computation/storage requirements of large-scale DNNs. Structured weight pruning methods have been proposed to overcome the limitation of irregular network structure and demonstrated actual GPU acceleration. However, the pruning ratio (degree of sparsity) and GPU acceleration are limited (to less than 50%) when accuracy needs to be maintained. In this work, we overcome pruning ratio and GPU acceleration limitations by proposing a unified, systematic framework of structured weight pruning for DNNs, named ADAM-ADMM (Adaptive Moment Estimation-Alternating Direction Method of Multipliers). It is a framework that can be used to induce different types of structured sparsity, such as filter-wise, channel-wise, and shape-wise sparsity, as well non-structured sparsity. The proposed framework incorporates stochastic gradient descent with ADMM, and can be understood as a dynamic regularization method in which the regularization target is analytically updated in each iteration. A significant improvement in weight pruning ratio is achieved without loss of accuracy, along with fast convergence rate. With a small sparsity degree of 33% on the convolutional layers, we achieve 1.64% accuracy enhancement for the AlexNet (CaffeNet) model. This is obtained by mitigation of overfitting. Without loss of accuracy on the AlexNet model, we achieve 2.6 times and 3.65 times average measured speedup on two GPUs, clearly outperforming the prior work. The average speedups reach 2.77 times and 7.5 times when allowing a moderate accuracy loss of 2%. In this case the model compression for convolutional layers is 13.2 times, corresponding to 10.5 times CPU speedup. Our models and codes are released at https://github.com/KaiqiZhang/ADAM-ADMM

A Systematic DNN Weight Pruning Framework using Alternating Direction Method of Multipliers

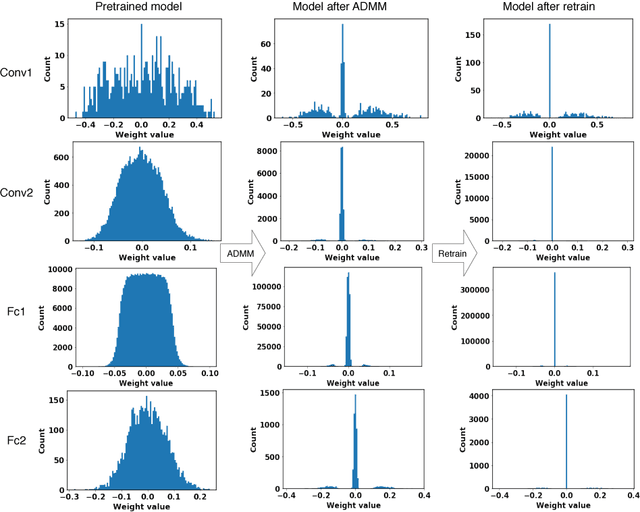
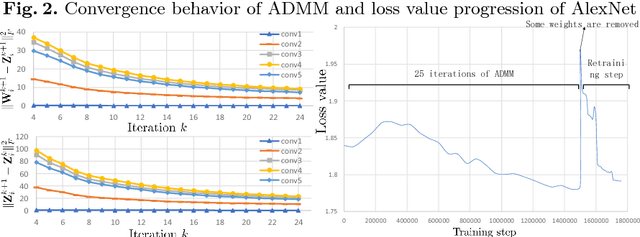
Weight pruning methods for deep neural networks (DNNs) have been investigated recently, but prior work in this area is mainly heuristic, iterative pruning, thereby lacking guarantees on the weight reduction ratio and convergence time. To mitigate these limitations, we present a systematic weight pruning framework of DNNs using the alternating direction method of multipliers (ADMM). We first formulate the weight pruning problem of DNNs as a nonconvex optimization problem with combinatorial constraints specifying the sparsity requirements, and then adopt the ADMM framework for systematic weight pruning. By using ADMM, the original nonconvex optimization problem is decomposed into two subproblems that are solved iteratively. One of these subproblems can be solved using stochastic gradient descent, the other can be solved analytically. Besides, our method achieves a fast convergence rate. The weight pruning results are very promising and consistently outperform the prior work. On the LeNet-5 model for the MNIST data set, we achieve 71.2 times weight reduction without accuracy loss. On the AlexNet model for the ImageNet data set, we achieve 21 times weight reduction without accuracy loss. When we focus on the convolutional layer pruning for computation reductions, we can reduce the total computation by five times compared with the prior work (achieving a total of 13.4 times weight reduction in convolutional layers). Our models and codes are released at https://github.com/KaiqiZhang/admm-pruning

Systematic Weight Pruning of DNNs using Alternating Direction Method of Multipliers

We present a systematic weight pruning framework of deep neural networks (DNNs) using the alternating direction method of multipliers (ADMM). We first formulate the weight pruning problem of DNNs as a constrained nonconvex optimization problem, and then adopt the ADMM framework for systematic weight pruning. We show that ADMM is highly suitable for weight pruning due to the computational efficiency it offers. We achieve a much higher compression ratio compared with prior work while maintaining the same test accuracy, together with a faster convergence rate. Our models are released at https://github.com/KaiqiZhang/admm-pruning

A Memristor-Based Optimization Framework for AI Applications

Memristors have recently received significant attention as ubiquitous device-level components for building a novel generation of computing systems. These devices have many promising features, such as non-volatility, low power consumption, high density, and excellent scalability. The ability to control and modify biasing voltages at the two terminals of memristors make them promising candidates to perform matrix-vector multiplications and solve systems of linear equations. In this article, we discuss how networks of memristors arranged in crossbar arrays can be used for efficiently solving optimization and machine learning problems. We introduce a new memristor-based optimization framework that combines the computational merit of memristor crossbars with the advantages of an operator splitting method, alternating direction method of multipliers (ADMM). Here, ADMM helps in splitting a complex optimization problem into subproblems that involve the solution of systems of linear equations. The capability of this framework is shown by applying it to linear programming, quadratic programming, and sparse optimization. In addition to ADMM, implementation of a customized power iteration (PI) method for eigenvalue/eigenvector computation using memristor crossbars is discussed. The memristor-based PI method can further be applied to principal component analysis (PCA). The use of memristor crossbars yields a significant speed-up in computation, and thus, we believe, has the potential to advance optimization and machine learning research in artificial intelligence (AI).