Learning Accurate, Efficient, and Interpretable MLPs on Multiplex Graphs via Node-wise Multi-View Ensemble Distillation

Multiplex graphs, with multiple edge types (graph views) among common nodes, provide richer structural semantics and better modeling capabilities. Multiplex Graph Neural Networks (MGNNs), typically comprising view-specific GNNs and a multi-view integration layer, have achieved advanced performance in various downstream tasks. However, their reliance on neighborhood aggregation poses challenges for deployment in latency-sensitive applications. Motivated by recent GNN-to-MLP knowledge distillation frameworks, we propose Multiplex Graph-Free Neural Networks (MGFNN and MGFNN+) to combine MGNNs' superior performance and MLPs' efficient inference via knowledge distillation. MGFNN directly trains student MLPs with node features as input and soft labels from teacher MGNNs as targets. MGFNN+ further employs a low-rank approximation-based reparameterization to learn node-wise coefficients, enabling adaptive knowledge ensemble from each view-specific GNN. This node-wise multi-view ensemble distillation strategy allows student MLPs to learn more informative multiplex semantic knowledge for different nodes. Experiments show that MGFNNs achieve average accuracy improvements of about 10% over vanilla MLPs and perform comparably or even better to teacher MGNNs (accurate); MGFNNs achieve a 35.40$\times$-89.14$\times$ speedup in inference over MGNNs (efficient); MGFNN+ adaptively assigns different coefficients for multi-view ensemble distillation regarding different nodes (interpretable).

Teaching MLPs to Master Heterogeneous Graph-Structured Knowledge for Efficient and Accurate Inference

Heterogeneous Graph Neural Networks (HGNNs) have achieved promising results in various heterogeneous graph learning tasks, owing to their superiority in capturing the intricate relationships and diverse relational semantics inherent in heterogeneous graph structures. However, the neighborhood-fetching latency incurred by structure dependency in HGNNs makes it challenging to deploy for latency-constrained applications that require fast inference. Inspired by recent GNN-to-MLP knowledge distillation frameworks, we introduce HG2M and HG2M+ to combine both HGNN's superior performance and MLP's efficient inference. HG2M directly trains student MLPs with node features as input and soft labels from teacher HGNNs as targets, and HG2M+ further distills reliable and heterogeneous semantic knowledge into student MLPs through reliable node distillation and reliable meta-path distillation. Experiments conducted on six heterogeneous graph datasets show that despite lacking structural dependencies, HG2Ms can still achieve competitive or even better performance than HGNNs and significantly outperform vanilla MLPs. Moreover, HG2Ms demonstrate a 379.24$\times$ speedup in inference over HGNNs on the large-scale IGB-3M-19 dataset, showcasing their ability for latency-sensitive deployments.

Negative-Free Self-Supervised Gaussian Embedding of Graphs

Graph Contrastive Learning (GCL) has recently emerged as a promising graph self-supervised learning framework for learning discriminative node representations without labels. The widely adopted objective function of GCL benefits from two key properties: \emph{alignment} and \emph{uniformity}, which align representations of positive node pairs while uniformly distributing all representations on the hypersphere. The uniformity property plays a critical role in preventing representation collapse and is achieved by pushing apart augmented views of different nodes (negative pairs). As such, existing GCL methods inherently rely on increasing the quantity and quality of negative samples, resulting in heavy computational demands, memory overhead, and potential class collision issues. In this study, we propose a negative-free objective to achieve uniformity, inspired by the fact that points distributed according to a normalized isotropic Gaussian are uniformly spread across the unit hypersphere. Therefore, we can minimize the distance between the distribution of learned representations and the isotropic Gaussian distribution to promote the uniformity of node representations. Our method also distinguishes itself from other approaches by eliminating the need for a parameterized mutual information estimator, an additional projector, asymmetric structures, and, crucially, negative samples. Extensive experiments over seven graph benchmarks demonstrate that our proposal achieves competitive performance with fewer parameters, shorter training times, and lower memory consumption compared to existing GCL methods.

Scalable and Adaptive Spectral Embedding for Attributed Graph Clustering

Attributed graph clustering, which aims to group the nodes of an attributed graph into disjoint clusters, has made promising advancements in recent years. However, most existing methods face challenges when applied to large graphs due to the expensive computational cost and high memory usage. In this paper, we introduce Scalable and Adaptive Spectral Embedding (SASE), a simple attributed graph clustering method devoid of parameter learning. SASE comprises three main components: node features smoothing via $k$-order simple graph convolution, scalable spectral clustering using random Fourier features, and adaptive order selection. With these designs, SASE not only effectively captures global cluster structures but also exhibits linear time and space complexity relative to the graph size. Empirical results demonstrate the superiority of SASE. For example, on the ArXiv dataset with 169K nodes and 1.17M edges, SASE achieves a 6.9\% improvement in ACC and a $5.87\times$ speedup compared to the runner-up, S3GC.

Bootstrap Latents of Nodes and Neighbors for Graph Self-Supervised Learning

Contrastive learning is a significant paradigm in graph self-supervised learning. However, it requires negative samples to prevent model collapse and learn discriminative representations. These negative samples inevitably lead to heavy computation, memory overhead and class collision, compromising the representation learning. Recent studies present that methods obviating negative samples can attain competitive performance and scalability enhancements, exemplified by bootstrapped graph latents (BGRL). However, BGRL neglects the inherent graph homophily, which provides valuable insights into underlying positive pairs. Our motivation arises from the observation that subtly introducing a few ground-truth positive pairs significantly improves BGRL. Although we can't obtain ground-truth positive pairs without labels under the self-supervised setting, edges in the graph can reflect noisy positive pairs, i.e., neighboring nodes often share the same label. Therefore, we propose to expand the positive pair set with node-neighbor pairs. Subsequently, we introduce a cross-attention module to predict the supportiveness score of a neighbor with respect to the anchor node. This score quantifies the positive support from each neighboring node, and is encoded into the training objective. Consequently, our method mitigates class collision from negative and noisy positive samples, concurrently enhancing intra-class compactness. Extensive experiments are conducted on five benchmark datasets and three downstream task node classification, node clustering, and node similarity search. The results demonstrate that our method generates node representations with enhanced intra-class compactness and achieves state-of-the-art performance.

Reliable Node Similarity Matrix Guided Contrastive Graph Clustering

Graph clustering, which involves the partitioning of nodes within a graph into disjoint clusters, holds significant importance for numerous subsequent applications. Recently, contrastive learning, known for utilizing supervisory information, has demonstrated encouraging results in deep graph clustering. This methodology facilitates the learning of favorable node representations for clustering by attracting positively correlated node pairs and distancing negatively correlated pairs within the representation space. Nevertheless, a significant limitation of existing methods is their inadequacy in thoroughly exploring node-wise similarity. For instance, some hypothesize that the node similarity matrix within the representation space is identical, ignoring the inherent semantic relationships among nodes. Given the fundamental role of instance similarity in clustering, our research investigates contrastive graph clustering from the perspective of the node similarity matrix. We argue that an ideal node similarity matrix within the representation space should accurately reflect the inherent semantic relationships among nodes, ensuring the preservation of semantic similarities in the learned representations. In response to this, we introduce a new framework, Reliable Node Similarity Matrix Guided Contrastive Graph Clustering (NS4GC), which estimates an approximately ideal node similarity matrix within the representation space to guide representation learning. Our method introduces node-neighbor alignment and semantic-aware sparsification, ensuring the node similarity matrix is both accurate and efficiently sparse. Comprehensive experiments conducted on $8$ real-world datasets affirm the efficacy of learning the node similarity matrix and the superior performance of NS4GC.

A novel robust meta-analysis model using the $t$ distribution for outlier accommodation and detection

Random effects meta-analysis model is an important tool for integrating results from multiple independent studies. However, the standard model is based on the assumption of normal distributions for both random effects and within-study errors, making it susceptible to outlying studies. Although robust modeling using the $t$ distribution is an appealing idea, the existing work, that explores the use of the $t$ distribution only for random effects, involves complicated numerical integration and numerical optimization. In this paper, a novel robust meta-analysis model using the $t$ distribution is proposed ($t$Meta). The novelty is that the marginal distribution of the effect size in $t$Meta follows the $t$ distribution, enabling that $t$Meta can simultaneously accommodate and detect outlying studies in a simple and adaptive manner. A simple and fast EM-type algorithm is developed for maximum likelihood estimation. Due to the mathematical tractability of the $t$ distribution, $t$Meta frees from numerical integration and allows for efficient optimization. Experiments on real data demonstrate that $t$Meta is compared favorably with related competitors in situations involving mild outliers. Moreover, in the presence of gross outliers, while related competitors may fail, $t$Meta continues to perform consistently and robustly.

A Safe Screening Rule with Bi-level Optimization of $ν$ Support Vector Machine

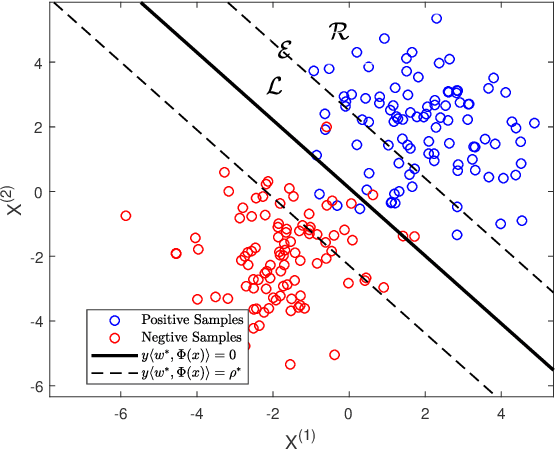
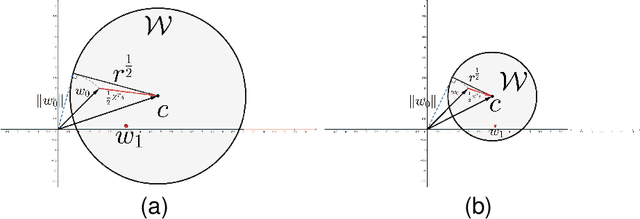
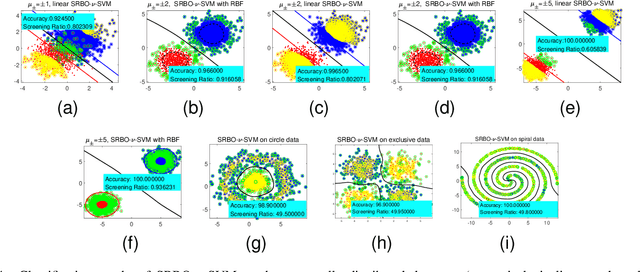
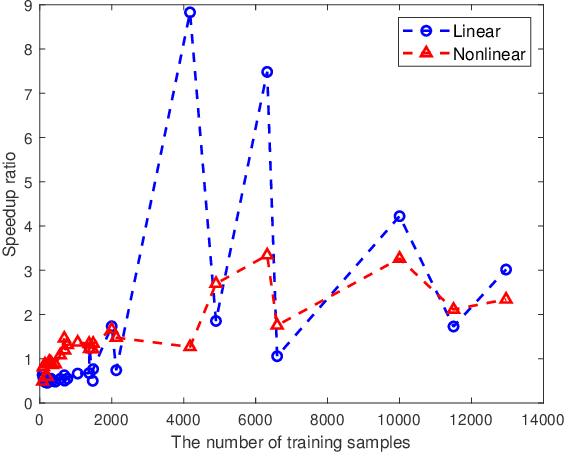
Support vector machine (SVM) has achieved many successes in machine learning, especially for a small sample problem. As a famous extension of the traditional SVM, the $\nu$ support vector machine ($\nu$-SVM) has shown outstanding performance due to its great model interpretability. However, it still faces challenges in training overhead for large-scale problems. To address this issue, we propose a safe screening rule with bi-level optimization for $\nu$-SVM (SRBO-$\nu$-SVM) which can screen out inactive samples before training and reduce the computational cost without sacrificing the prediction accuracy. Our SRBO-$\nu$-SVM is strictly deduced by integrating the Karush-Kuhn-Tucker (KKT) conditions, the variational inequalities of convex problems and the $\nu$-property. Furthermore, we develop an efficient dual coordinate descent method (DCDM) to further improve computational speed. Finally, a unified framework for SRBO is proposed to accelerate many SVM-type models, and it is successfully applied to one-class SVM. Experimental results on 6 artificial data sets and 30 benchmark data sets have verified the effectiveness and safety of our proposed methods in supervised and unsupervised tasks.

Robust bilinear factor analysis based on the matrix-variate $t$ distribution

Factor Analysis based on multivariate $t$ distribution ($t$fa) is a useful robust tool for extracting common factors on heavy-tailed or contaminated data. However, $t$fa is only applicable to vector data. When $t$fa is applied to matrix data, it is common to first vectorize the matrix observations. This introduces two challenges for $t$fa: (i) the inherent matrix structure of the data is broken, and (ii) robustness may be lost, as vectorized matrix data typically results in a high data dimension, which could easily lead to the breakdown of $t$fa. To address these issues, starting from the intrinsic matrix structure of matrix data, a novel robust factor analysis model, namely bilinear factor analysis built on the matrix-variate $t$ distribution ($t$bfa), is proposed in this paper. The novelty is that it is capable to simultaneously extract common factors for both row and column variables of interest on heavy-tailed or contaminated matrix data. Two efficient algorithms for maximum likelihood estimation of $t$bfa are developed. Closed-form expression for the Fisher information matrix to calculate the accuracy of parameter estimates are derived. Empirical studies are conducted to understand the proposed $t$bfa model and compare with related competitors. The results demonstrate the superiority and practicality of $t$bfa. Importantly, $t$bfa exhibits a significantly higher breakdown point than $t$fa, making it more suitable for matrix data.

Choosing the number of factors in factor analysis with incomplete data via a hierarchical Bayesian information criterion

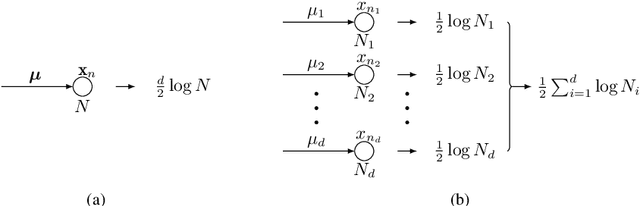
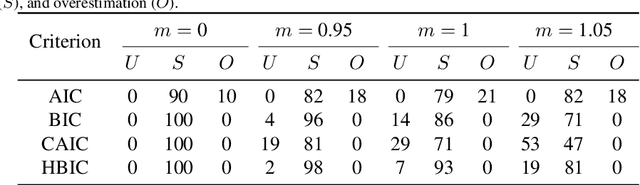
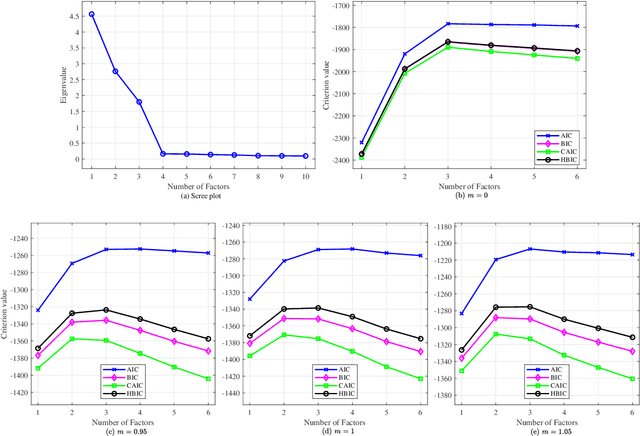
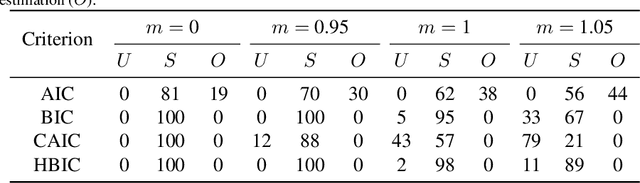
The Bayesian information criterion (BIC), defined as the observed data log likelihood minus a penalty term based on the sample size $N$, is a popular model selection criterion for factor analysis with complete data. This definition has also been suggested for incomplete data. However, the penalty term based on the `complete' sample size $N$ is the same no matter whether in a complete or incomplete data case. For incomplete data, there are often only $N_i<N$ observations for variable $i$, which means that using the `complete' sample size $N$ implausibly ignores the amounts of missing information inherent in incomplete data. Given this observation, a novel criterion called hierarchical BIC (HBIC) for factor analysis with incomplete data is proposed. The novelty is that it only uses the actual amounts of observed information, namely $N_i$'s, in the penalty term. Theoretically, it is shown that HBIC is a large sample approximation of variational Bayesian (VB) lower bound, and BIC is a further approximation of HBIC, which means that HBIC shares the theoretical consistency of BIC. Experiments on synthetic and real data sets are conducted to access the finite sample performance of HBIC, BIC, and related criteria with various missing rates. The results show that HBIC and BIC perform similarly when the missing rate is small, but HBIC is more accurate when the missing rate is not small.