A novel robust meta-analysis model using the $t$ distribution for outlier accommodation and detection

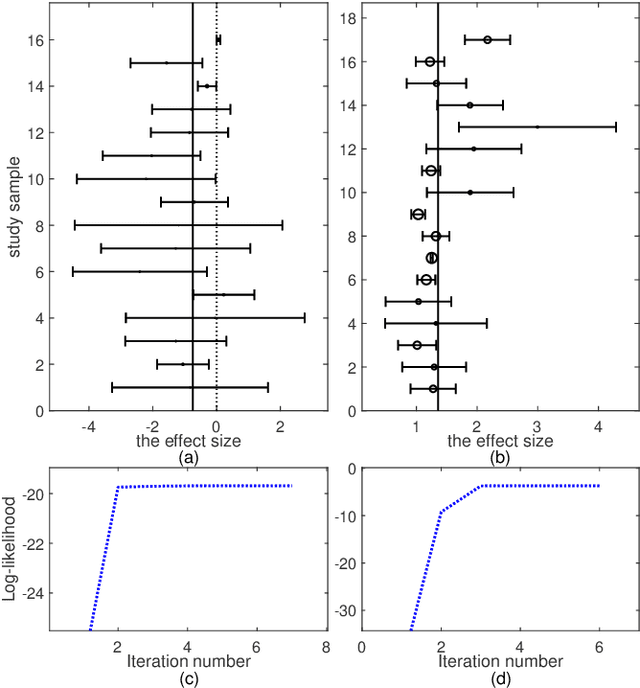
Random effects meta-analysis model is an important tool for integrating results from multiple independent studies. However, the standard model is based on the assumption of normal distributions for both random effects and within-study errors, making it susceptible to outlying studies. Although robust modeling using the $t$ distribution is an appealing idea, the existing work, that explores the use of the $t$ distribution only for random effects, involves complicated numerical integration and numerical optimization. In this paper, a novel robust meta-analysis model using the $t$ distribution is proposed ($t$Meta). The novelty is that the marginal distribution of the effect size in $t$Meta follows the $t$ distribution, enabling that $t$Meta can simultaneously accommodate and detect outlying studies in a simple and adaptive manner. A simple and fast EM-type algorithm is developed for maximum likelihood estimation. Due to the mathematical tractability of the $t$ distribution, $t$Meta frees from numerical integration and allows for efficient optimization. Experiments on real data demonstrate that $t$Meta is compared favorably with related competitors in situations involving mild outliers. Moreover, in the presence of gross outliers, while related competitors may fail, $t$Meta continues to perform consistently and robustly.

Robust bilinear factor analysis based on the matrix-variate $t$ distribution

Factor Analysis based on multivariate $t$ distribution ($t$fa) is a useful robust tool for extracting common factors on heavy-tailed or contaminated data. However, $t$fa is only applicable to vector data. When $t$fa is applied to matrix data, it is common to first vectorize the matrix observations. This introduces two challenges for $t$fa: (i) the inherent matrix structure of the data is broken, and (ii) robustness may be lost, as vectorized matrix data typically results in a high data dimension, which could easily lead to the breakdown of $t$fa. To address these issues, starting from the intrinsic matrix structure of matrix data, a novel robust factor analysis model, namely bilinear factor analysis built on the matrix-variate $t$ distribution ($t$bfa), is proposed in this paper. The novelty is that it is capable to simultaneously extract common factors for both row and column variables of interest on heavy-tailed or contaminated matrix data. Two efficient algorithms for maximum likelihood estimation of $t$bfa are developed. Closed-form expression for the Fisher information matrix to calculate the accuracy of parameter estimates are derived. Empirical studies are conducted to understand the proposed $t$bfa model and compare with related competitors. The results demonstrate the superiority and practicality of $t$bfa. Importantly, $t$bfa exhibits a significantly higher breakdown point than $t$fa, making it more suitable for matrix data.