Negative-Free Self-Supervised Gaussian Embedding of Graphs
Paper and Code
Nov 02, 2024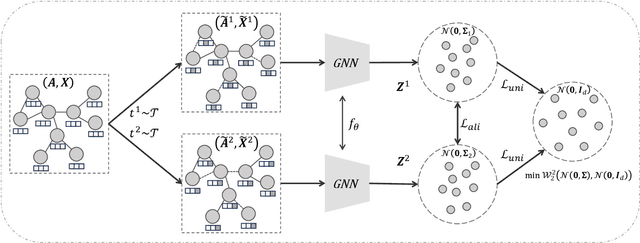
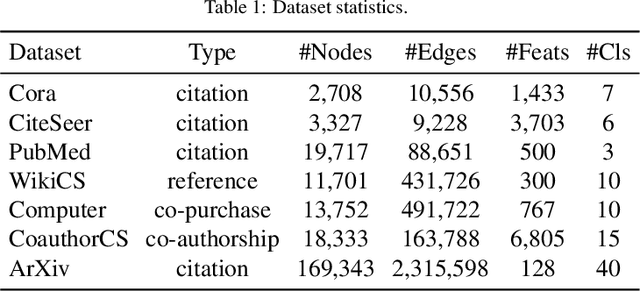
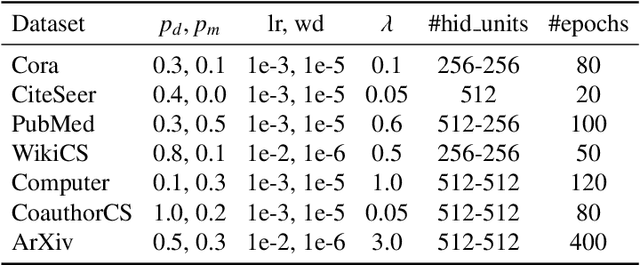
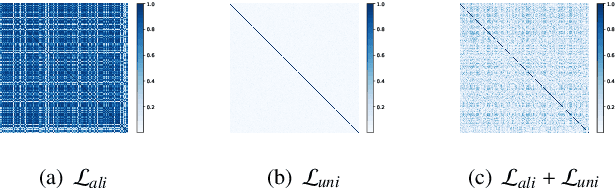
Graph Contrastive Learning (GCL) has recently emerged as a promising graph self-supervised learning framework for learning discriminative node representations without labels. The widely adopted objective function of GCL benefits from two key properties: \emph{alignment} and \emph{uniformity}, which align representations of positive node pairs while uniformly distributing all representations on the hypersphere. The uniformity property plays a critical role in preventing representation collapse and is achieved by pushing apart augmented views of different nodes (negative pairs). As such, existing GCL methods inherently rely on increasing the quantity and quality of negative samples, resulting in heavy computational demands, memory overhead, and potential class collision issues. In this study, we propose a negative-free objective to achieve uniformity, inspired by the fact that points distributed according to a normalized isotropic Gaussian are uniformly spread across the unit hypersphere. Therefore, we can minimize the distance between the distribution of learned representations and the isotropic Gaussian distribution to promote the uniformity of node representations. Our method also distinguishes itself from other approaches by eliminating the need for a parameterized mutual information estimator, an additional projector, asymmetric structures, and, crucially, negative samples. Extensive experiments over seven graph benchmarks demonstrate that our proposal achieves competitive performance with fewer parameters, shorter training times, and lower memory consumption compared to existing GCL methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge