Reliable Node Similarity Matrix Guided Contrastive Graph Clustering
Paper and Code
Aug 07, 2024
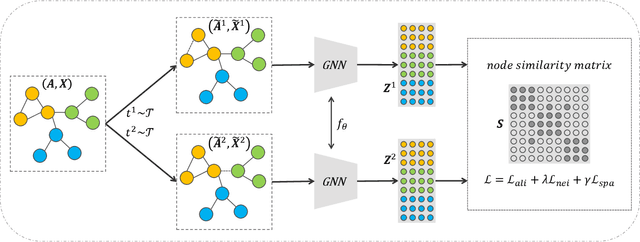
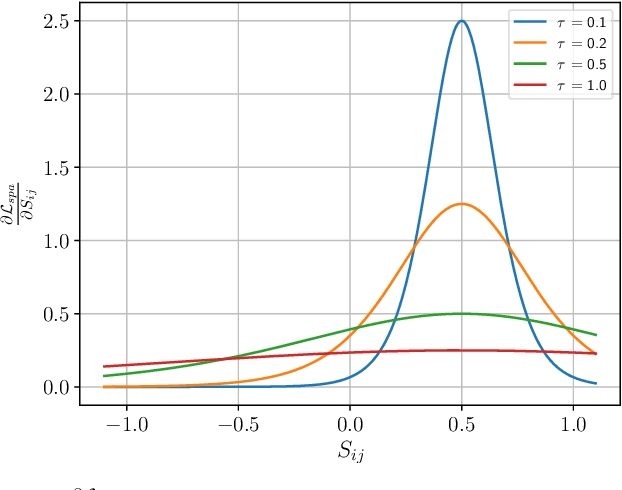
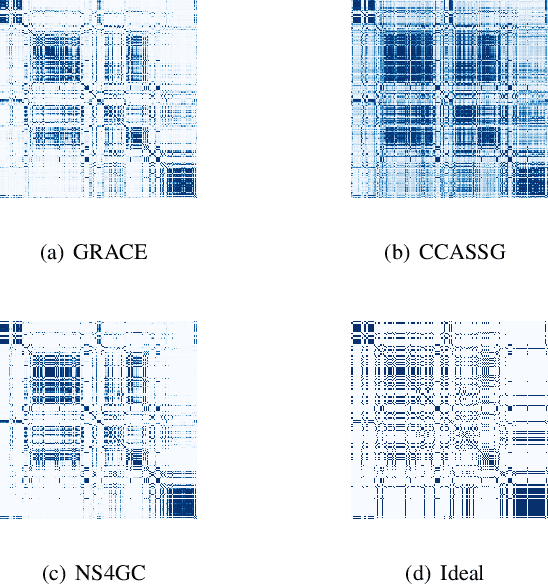
Graph clustering, which involves the partitioning of nodes within a graph into disjoint clusters, holds significant importance for numerous subsequent applications. Recently, contrastive learning, known for utilizing supervisory information, has demonstrated encouraging results in deep graph clustering. This methodology facilitates the learning of favorable node representations for clustering by attracting positively correlated node pairs and distancing negatively correlated pairs within the representation space. Nevertheless, a significant limitation of existing methods is their inadequacy in thoroughly exploring node-wise similarity. For instance, some hypothesize that the node similarity matrix within the representation space is identical, ignoring the inherent semantic relationships among nodes. Given the fundamental role of instance similarity in clustering, our research investigates contrastive graph clustering from the perspective of the node similarity matrix. We argue that an ideal node similarity matrix within the representation space should accurately reflect the inherent semantic relationships among nodes, ensuring the preservation of semantic similarities in the learned representations. In response to this, we introduce a new framework, Reliable Node Similarity Matrix Guided Contrastive Graph Clustering (NS4GC), which estimates an approximately ideal node similarity matrix within the representation space to guide representation learning. Our method introduces node-neighbor alignment and semantic-aware sparsification, ensuring the node similarity matrix is both accurate and efficiently sparse. Comprehensive experiments conducted on $8$ real-world datasets affirm the efficacy of learning the node similarity matrix and the superior performance of NS4GC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge