Choosing the number of factors in factor analysis with incomplete data via a hierarchical Bayesian information criterion

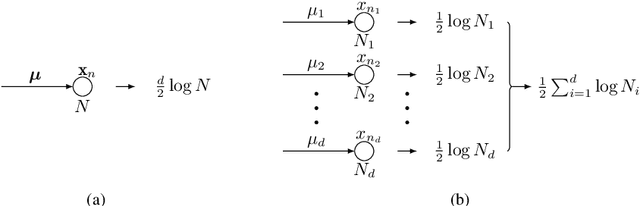
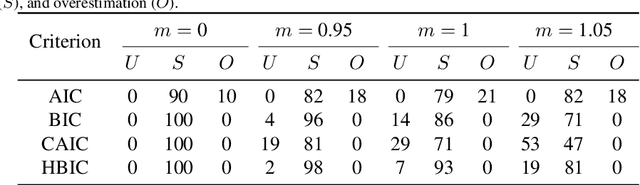
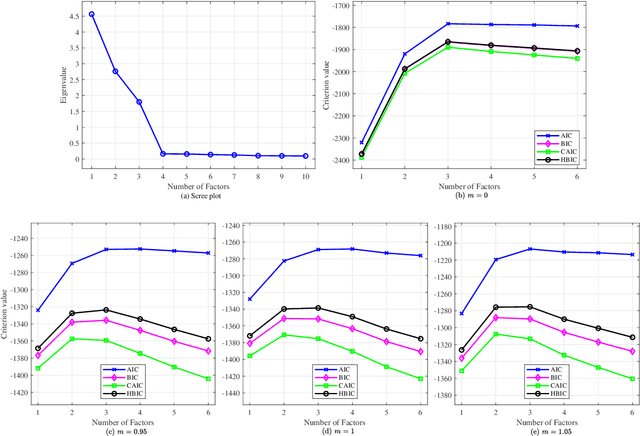
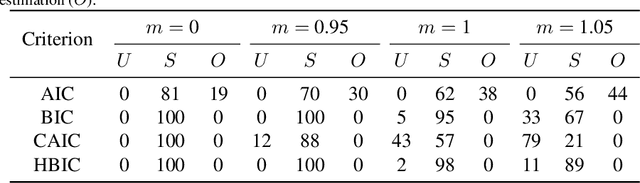
The Bayesian information criterion (BIC), defined as the observed data log likelihood minus a penalty term based on the sample size $N$, is a popular model selection criterion for factor analysis with complete data. This definition has also been suggested for incomplete data. However, the penalty term based on the `complete' sample size $N$ is the same no matter whether in a complete or incomplete data case. For incomplete data, there are often only $N_i<N$ observations for variable $i$, which means that using the `complete' sample size $N$ implausibly ignores the amounts of missing information inherent in incomplete data. Given this observation, a novel criterion called hierarchical BIC (HBIC) for factor analysis with incomplete data is proposed. The novelty is that it only uses the actual amounts of observed information, namely $N_i$'s, in the penalty term. Theoretically, it is shown that HBIC is a large sample approximation of variational Bayesian (VB) lower bound, and BIC is a further approximation of HBIC, which means that HBIC shares the theoretical consistency of BIC. Experiments on synthetic and real data sets are conducted to access the finite sample performance of HBIC, BIC, and related criteria with various missing rates. The results show that HBIC and BIC perform similarly when the missing rate is small, but HBIC is more accurate when the missing rate is not small.

Regularized Bilinear Discriminant Analysis for Multivariate Time Series Data

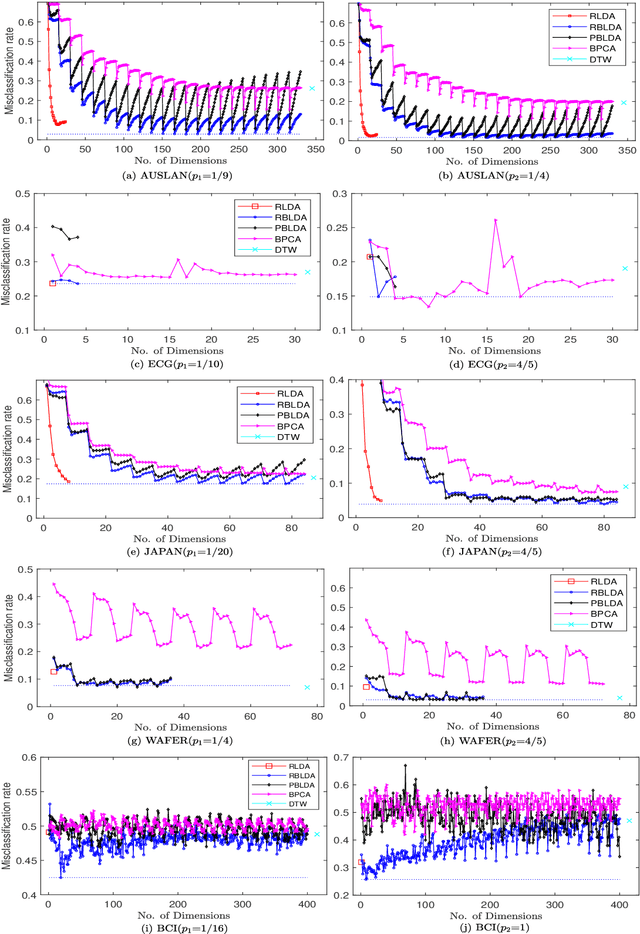
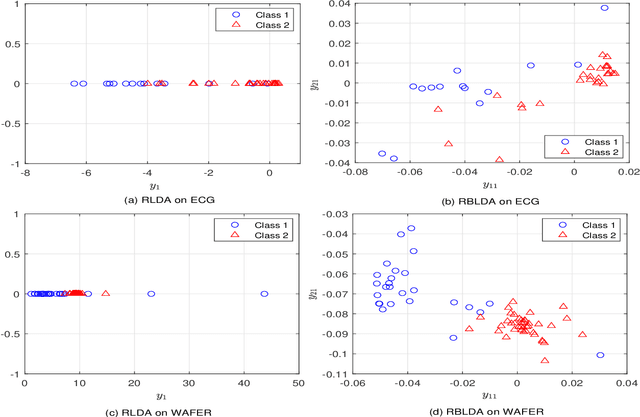
In recent years, the methods on matrix-based or bilinear discriminant analysis (BLDA) have received much attention. Despite their advantages, it has been reported that the traditional vector-based regularized LDA (RLDA) is still quite competitive and could outperform BLDA on some benchmark datasets. Nevertheless, it is also noted that this finding is mainly limited to image data. In this paper, we propose regularized BLDA (RBLDA) and further explore the comparison between RLDA and RBLDA on another type of matrix data, namely multivariate time series (MTS). Unlike image data, MTS typically consists of multiple variables measured at different time points. Although many methods for MTS data classification exist within the literature, there is relatively little work in exploring the matrix data structure of MTS data. Moreover, the existing BLDA can not be performed when one of its within-class matrices is singular. To address the two problems, we propose RBLDA for MTS data classification, where each of the two within-class matrices is regularized via one parameter. We develop an efficient implementation of RBLDA and an efficient model selection algorithm with which the cross validation procedure for RBLDA can be performed efficiently. Experiments on a number of real MTS data sets are conducted to evaluate the proposed algorithm and compare RBLDA with several closely related methods, including RLDA and BLDA. The results reveal that RBLDA achieves the best overall recognition performance and the proposed model selection algorithm is efficient; Moreover, RBLDA can produce better visualization of MTS data than RLDA.