Beyond 'Aha!': Toward Systematic Meta-Abilities Alignment in Large Reasoning Models

Large reasoning models (LRMs) already possess a latent capacity for long chain-of-thought reasoning. Prior work has shown that outcome-based reinforcement learning (RL) can incidentally elicit advanced reasoning behaviors such as self-correction, backtracking, and verification phenomena often referred to as the model's "aha moment". However, the timing and consistency of these emergent behaviors remain unpredictable and uncontrollable, limiting the scalability and reliability of LRMs' reasoning capabilities. To address these limitations, we move beyond reliance on prompts and coincidental "aha moments". Instead, we explicitly align models with three meta-abilities: deduction, induction, and abduction, using automatically generated, self-verifiable tasks. Our three stage-pipeline individual alignment, parameter-space merging, and domain-specific reinforcement learning, boosting performance by over 10\% relative to instruction-tuned baselines. Furthermore, domain-specific RL from the aligned checkpoint yields an additional 2\% average gain in the performance ceiling across math, coding, and science benchmarks, demonstrating that explicit meta-ability alignment offers a scalable and dependable foundation for reasoning. Code is available at: https://github.com/zhiyuanhubj/Meta-Ability-Alignment

Scalable Chain of Thoughts via Elastic Reasoning

Large reasoning models (LRMs) have achieved remarkable progress on complex tasks by generating extended chains of thought (CoT). However, their uncontrolled output lengths pose significant challenges for real-world deployment, where inference-time budgets on tokens, latency, or compute are strictly constrained. We propose Elastic Reasoning, a novel framework for scalable chain of thoughts that explicitly separates reasoning into two phases--thinking and solution--with independently allocated budgets. At test time, Elastic Reasoning prioritize that completeness of solution segments, significantly improving reliability under tight resource constraints. To train models that are robust to truncated thinking, we introduce a lightweight budget-constrained rollout strategy, integrated into GRPO, which teaches the model to reason adaptively when the thinking process is cut short and generalizes effectively to unseen budget constraints without additional training. Empirical results on mathematical (AIME, MATH500) and programming (LiveCodeBench, Codeforces) benchmarks demonstrate that Elastic Reasoning performs robustly under strict budget constraints, while incurring significantly lower training cost than baseline methods. Remarkably, our approach also produces more concise and efficient reasoning even in unconstrained settings. Elastic Reasoning offers a principled and practical solution to the pressing challenge of controllable reasoning at scale.

Optimizing Chain-of-Thought Reasoners via Gradient Variance Minimization in Rejection Sampling and RL

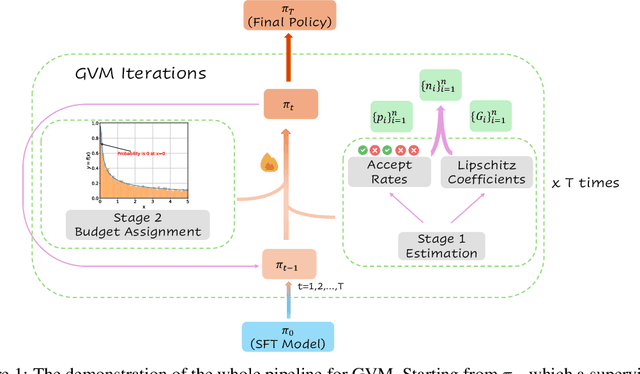
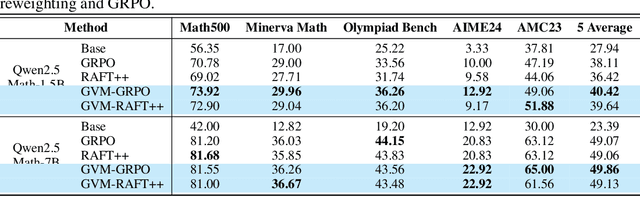
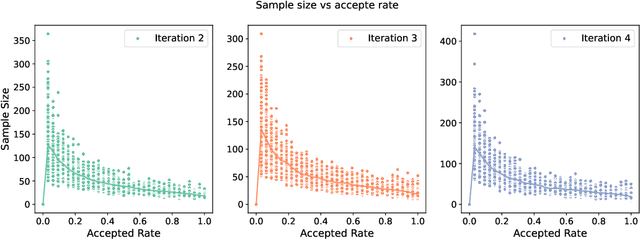
Chain-of-thought (CoT) reasoning in large language models (LLMs) can be formalized as a latent variable problem, where the model needs to generate intermediate reasoning steps. While prior approaches such as iterative reward-ranked fine-tuning (RAFT) have relied on such formulations, they typically apply uniform inference budgets across prompts, which fails to account for variability in difficulty and convergence behavior. This work identifies the main bottleneck in CoT training as inefficient stochastic gradient estimation due to static sampling strategies. We propose GVM-RAFT, a prompt-specific Dynamic Sample Allocation Strategy designed to minimize stochastic gradient variance under a computational budget constraint. The method dynamically allocates computational resources by monitoring prompt acceptance rates and stochastic gradient norms, ensuring that the resulting gradient variance is minimized. Our theoretical analysis shows that the proposed dynamic sampling strategy leads to accelerated convergence guarantees under suitable conditions. Experiments on mathematical reasoning show that GVM-RAFT achieves a 2-4x speedup and considerable accuracy improvements over vanilla RAFT. The proposed dynamic sampling strategy is general and can be incorporated into other reinforcement learning algorithms, such as GRPO, leading to similar improvements in convergence and test accuracy. Our code is available at https://github.com/RLHFlow/GVM.

A Minimalist Approach to LLM Reasoning: from Rejection Sampling to Reinforce

Reinforcement learning (RL) has become a prevailing approach for fine-tuning large language models (LLMs) on complex reasoning tasks. Among recent methods, GRPO stands out for its empirical success in training models such as DeepSeek-R1, yet the sources of its effectiveness remain poorly understood. In this work, we revisit GRPO from a reinforce-like algorithm perspective and analyze its core components. Surprisingly, we find that a simple rejection sampling baseline, RAFT, which trains only on positively rewarded samples, yields competitive performance than GRPO and PPO. Our ablation studies reveal that GRPO's main advantage arises from discarding prompts with entirely incorrect responses, rather than from its reward normalization. Motivated by this insight, we propose Reinforce-Rej, a minimal extension of policy gradient that filters both entirely incorrect and entirely correct samples. Reinforce-Rej improves KL efficiency and stability, serving as a lightweight yet effective alternative to more complex RL algorithms. We advocate RAFT as a robust and interpretable baseline, and suggest that future advances should focus on more principled designs for incorporating negative samples, rather than relying on them indiscriminately. Our findings provide guidance for future work in reward-based LLM post-training.

Reward Models Identify Consistency, Not Causality

Reward models (RMs) play a crucial role in aligning large language models (LLMs) with human preferences and enhancing reasoning quality. Traditionally, RMs are trained to rank candidate outputs based on their correctness and coherence. However, in this work, we present several surprising findings that challenge common assumptions about RM behavior. Our analysis reveals that state-of-the-art reward models prioritize structural consistency over causal correctness. Specifically, removing the problem statement has minimal impact on reward scores, whereas altering numerical values or disrupting the reasoning flow significantly affects RM outputs. Furthermore, RMs exhibit a strong dependence on complete reasoning trajectories truncated or incomplete steps lead to significant variations in reward assignments, indicating that RMs primarily rely on learned reasoning patterns rather than explicit problem comprehension. These findings hold across multiple architectures, datasets, and tasks, leading to three key insights: (1) RMs primarily assess coherence rather than true reasoning quality; (2) The role of explicit problem comprehension in reward assignment is overstated; (3) Current RMs may be more effective at ranking responses than verifying logical validity. Our results suggest a fundamental limitation in existing reward modeling approaches, emphasizing the need for a shift toward causality-aware reward models that go beyond consistency-driven evaluation.

BOLT: Bootstrap Long Chain-of-Thought in Language Models without Distillation

Large language models (LLMs), such as o1 from OpenAI, have demonstrated remarkable reasoning capabilities. o1 generates a long chain-of-thought (LongCoT) before answering a question. LongCoT allows LLMs to analyze problems, devise plans, reflect, and backtrack effectively. These actions empower LLM to solve complex problems. After the release of o1, many teams have attempted to replicate its LongCoT and reasoning capabilities. In terms of methods, they primarily rely on knowledge distillation with data from existing models with LongCoT capacities (e.g., OpenAI-o1, Qwen-QwQ, DeepSeek-R1-Preview), leaving significant uncertainties on systematically developing such reasoning abilities. In terms of data domains, these works focus narrowly on math while a few others include coding, limiting their generalizability. This paper introduces a novel approach to enable LLM's LongCoT capacity without distillation from o1-like models or expensive human annotations, where we bootstrap LongCoT (BOLT) from a standard instruct model. BOLT involves three stages: 1) LongCoT data bootstrapping with in-context learning on a standard instruct model; 2) LongCoT supervised finetuning; 3) online training to further refine LongCoT capacities. In BOLT, only a few in-context examples need to be constructed during the bootstrapping stage; in our experiments, we created 10 examples, demonstrating the feasibility of this approach. We use Llama-3.1-70B-Instruct to bootstrap LongCoT and apply our method to various model scales (7B, 8B, 70B). We achieve impressive performance on a variety of benchmarks, Arena-Hard, MT-Bench, WildBench, ZebraLogic, MATH500, which evaluate diverse task-solving and reasoning capabilities.

Reward-Guided Speculative Decoding for Efficient LLM Reasoning

We introduce Reward-Guided Speculative Decoding (RSD), a novel framework aimed at improving the efficiency of inference in large language models (LLMs). RSD synergistically combines a lightweight draft model with a more powerful target model, incorporating a controlled bias to prioritize high-reward outputs, in contrast to existing speculative decoding methods that enforce strict unbiasedness. RSD employs a process reward model to evaluate intermediate decoding steps and dynamically decide whether to invoke the target model, optimizing the trade-off between computational cost and output quality. We theoretically demonstrate that a threshold-based mixture strategy achieves an optimal balance between resource utilization and performance. Extensive evaluations on challenging reasoning benchmarks, including Olympiad-level tasks, show that RSD delivers significant efficiency gains against decoding with the target model only (up to 4.4x fewer FLOPs), while achieving significant better accuracy than parallel decoding method on average (up to +3.5). These results highlight RSD as a robust and cost-effective approach for deploying LLMs in resource-intensive scenarios.

Offline Reinforcement Learning for LLM Multi-Step Reasoning

Improving the multi-step reasoning ability of large language models (LLMs) with offline reinforcement learning (RL) is essential for quickly adapting them to complex tasks. While Direct Preference Optimization (DPO) has shown promise in aligning LLMs with human preferences, it is less suitable for multi-step reasoning tasks because (1) DPO relies on paired preference data, which is not readily available for multi-step reasoning tasks, and (2) it treats all tokens uniformly, making it ineffective for credit assignment in multi-step reasoning tasks, which often come with sparse reward. In this work, we propose OREO (Offline Reasoning Optimization), an offline RL method for enhancing LLM multi-step reasoning. Building on insights from previous works of maximum entropy reinforcement learning, it jointly learns a policy model and value function by optimizing the soft Bellman Equation. We show in principle that it reduces the need to collect pairwise data and enables better credit assignment. Empirically, OREO surpasses existing offline learning methods on multi-step reasoning benchmarks, including mathematical reasoning tasks (GSM8K, MATH) and embodied agent control (ALFWorld). The approach can be extended to a multi-iteration framework when additional resources are available. Furthermore, the learned value function can be leveraged to guide the tree search for free, which can further boost performance during test time.

Entropy-Regularized Process Reward Model

Large language models (LLMs) have shown promise in performing complex multi-step reasoning, yet they continue to struggle with mathematical reasoning, often making systematic errors. A promising solution is reinforcement learning (RL) guided by reward models, particularly those focusing on process rewards, which score each intermediate step rather than solely evaluating the final outcome. This approach is more effective at guiding policy models towards correct reasoning trajectories. In this work, we propose an entropy-regularized process reward model (ER-PRM) that integrates KL-regularized Markov Decision Processes (MDP) to balance policy optimization with the need to prevent the policy from shifting too far from its initial distribution. We derive a novel reward construction method based on the theoretical results. Our theoretical analysis shows that we could derive the optimal reward model from the initial policy sampling. Our empirical experiments on the MATH and GSM8K benchmarks demonstrate that ER-PRM consistently outperforms existing process reward models, achieving 1% improvement on GSM8K and 2-3% improvement on MATH under best-of-N evaluation, and more than 1% improvement under RLHF. These results highlight the efficacy of entropy-regularization in enhancing LLMs' reasoning capabilities.

Automatic Curriculum Expert Iteration for Reliable LLM Reasoning

Hallucinations (i.e., generating plausible but inaccurate content) and laziness (i.e. excessive refusals or defaulting to "I don't know") persist as major challenges in LLM reasoning. Current efforts to reduce hallucinations primarily focus on factual errors in knowledge-grounded tasks, often neglecting hallucinations related to faulty reasoning. Meanwhile, some approaches render LLMs overly conservative, limiting their problem-solving capabilities. To mitigate hallucination and laziness in reasoning tasks, we propose Automatic Curriculum Expert Iteration (Auto-CEI) to enhance LLM reasoning and align responses to the model's capabilities--assertively answering within its limits and declining when tasks exceed them. In our method, Expert Iteration explores the reasoning trajectories near the LLM policy, guiding incorrect paths back on track to reduce compounding errors and improve robustness; it also promotes appropriate "I don't know" responses after sufficient reasoning attempts. The curriculum automatically adjusts rewards, incentivizing extended reasoning before acknowledging incapability, thereby pushing the limits of LLM reasoning and aligning its behaviour with these limits. We compare Auto-CEI with various SOTA baselines across logical reasoning, mathematics, and planning tasks, where Auto-CEI achieves superior alignment by effectively balancing assertiveness and conservativeness.