Xuebo Zhang
EDEN: Efficient Dual-Layer Exploration Planning for Fast UAV Autonomous Exploration in Large 3-D Environments
Jun 05, 2025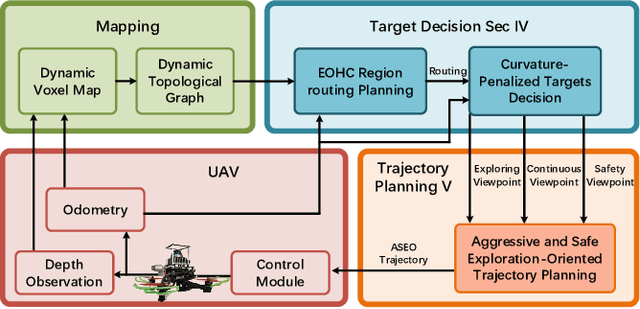
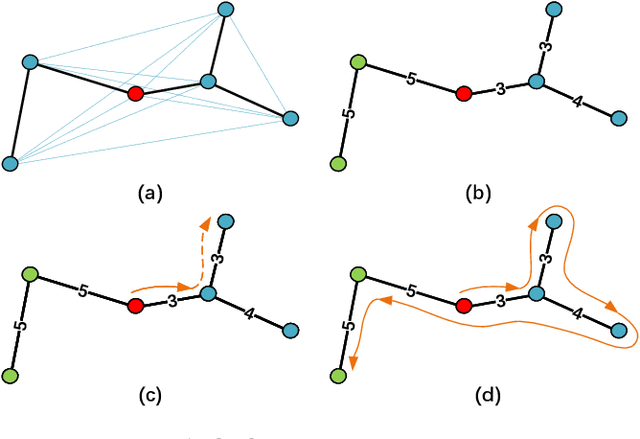
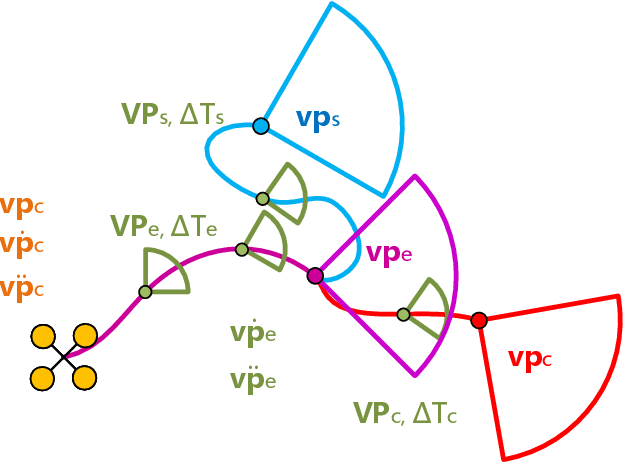

Abstract:Efficient autonomous exploration in large-scale environments remains challenging due to the high planning computational cost and low-speed maneuvers. In this paper, we propose a fast and computationally efficient dual-layer exploration planning method. The insight of our dual-layer method is efficiently finding an acceptable long-term region routing and greedily exploring the target in the region of the first routing area with high speed. Specifically, the proposed method finds the long-term area routing through an approximate algorithm to ensure real-time planning in large-scale environments. Then, the viewpoint in the first routing region with the lowest curvature-penalized cost, which can effectively reduce decelerations caused by sharp turn motions, will be chosen as the next exploration target. To further speed up the exploration, we adopt an aggressive and safe exploration-oriented trajectory to enhance exploration continuity. The proposed method is compared to state-of-the-art methods in challenging simulation environments. The results show that the proposed method outperforms other methods in terms of exploration efficiency, computational cost, and trajectory speed. We also conduct real-world experiments to validate the effectiveness of the proposed method. The code will be open-sourced.
Retrieval Augmented Learning: A Retrial-based Large Language Model Self-Supervised Learning and Autonomous Knowledge Generation
May 02, 2025Abstract:The lack of domain-specific data in the pre-training of Large Language Models (LLMs) severely limits LLM-based decision systems in specialized applications, while post-training a model in the scenarios requires significant computational resources. In this paper, we present Retrial-Augmented Learning (RAL), a reward-free self-supervised learning framework for LLMs that operates without model training. By developing Retrieval-Augmented Generation (RAG) into a module for organizing intermediate data, we realized a three-stage autonomous knowledge generation of proposing a hypothesis, validating the hypothesis, and generating the knowledge. The method is evaluated in the LLM-PySC2 environment, a representative decision-making platform that combines sufficient complexity with domain-specific knowledge requirements. Experiments demonstrate that the proposed method effectively reduces hallucination by generating and utilizing validated knowledge, and increases decision-making performance at an extremely low cost. Meanwhile, the approach exhibits potential in out-of-distribution(OOD) tasks, robustness, and transferability, making it a cost-friendly but effective solution for decision-making problems and autonomous knowledge generation.
FSMP: A Frontier-Sampling-Mixed Planner for Fast Autonomous Exploration of Complex and Large 3-D Environments
Feb 28, 2025



Abstract:In this paper, we propose a systematic framework for fast exploration of complex and large 3-D environments using micro aerial vehicles (MAVs). The key insight is the organic integration of the frontier-based and sampling-based strategies that can achieve rapid global exploration of the environment. Specifically, a field-of-view-based (FOV) frontier detector with the guarantee of completeness and soundness is devised for identifying 3-D map frontiers. Different from random sampling-based methods, the deterministic sampling technique is employed to build and maintain an incremental road map based on the recorded sensor FOVs and newly detected frontiers. With the resulting road map, we propose a two-stage path planner. First, it quickly computes the global optimal exploration path on the road map using the lazy evaluation strategy. Then, the best exploration path is smoothed for further improving the exploration efficiency. We validate the proposed method both in simulation and real-world experiments. The comparative results demonstrate the promising performance of our planner in terms of exploration efficiency, computational time, and explored volume.
Reflection of Episodes: Learning to Play Game from Expert and Self Experiences
Feb 19, 2025

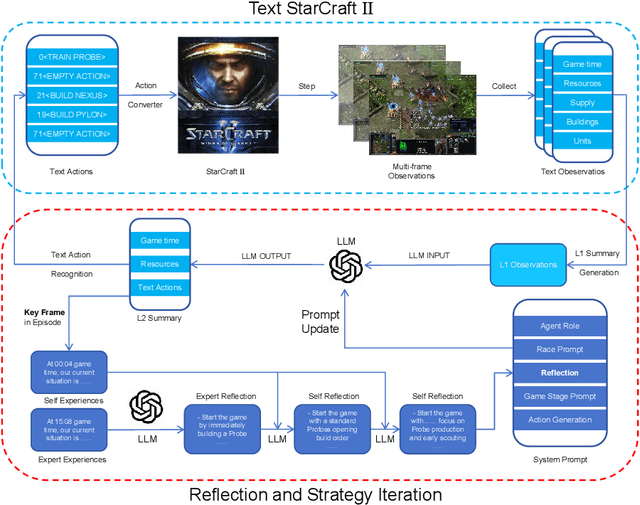

Abstract:StarCraft II is a complex and dynamic real-time strategy (RTS) game environment, which is very suitable for artificial intelligence and reinforcement learning research. To address the problem of Large Language Model(LLM) learning in complex environments through self-reflection, we propose a Reflection of Episodes(ROE) framework based on expert experience and self-experience. This framework first obtains key information in the game through a keyframe selection method, then makes decisions based on expert experience and self-experience. After a game is completed, it reflects on the previous experience to obtain new self-experience. Finally, in the experiment, our method beat the robot under the Very Hard difficulty in TextStarCraft II. We analyze the data of the LLM in the process of the game in detail, verified its effectiveness.
LLM-PySC2: Starcraft II learning environment for Large Language Models
Nov 08, 2024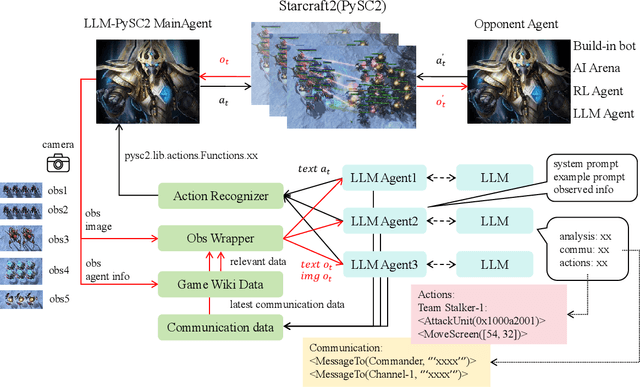
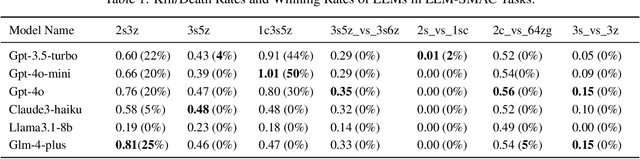
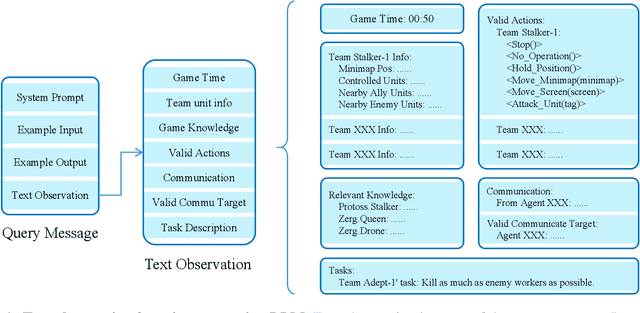

Abstract:This paper introduces a new environment LLM-PySC2 (the Large Language Model StarCraft II Learning Environment), a platform derived from DeepMind's StarCraft II Learning Environment that serves to develop Large Language Models (LLMs) based decision-making methodologies. This environment is the first to offer the complete StarCraft II action space, multi-modal observation interfaces, and a structured game knowledge database, which are seamlessly connected with various LLMs to facilitate the research of LLMs-based decision-making. To further support multi-agent research, we developed an LLM collaborative framework that supports multi-agent concurrent queries and multi-agent communication. In our experiments, the LLM-PySC2 environment is adapted to be compatible with the StarCraft Multi-Agent Challenge (SMAC) task group and provided eight new scenarios focused on macro-decision abilities. We evaluated nine mainstream LLMs in the experiments, and results show that sufficient parameters are necessary for LLMs to make decisions, but improving reasoning ability does not directly lead to better decision-making outcomes. Our findings further indicate the importance of enabling large models to learn autonomously in the deployment environment through parameter training or train-free learning techniques. Ultimately, we expect that the LLM-PySC2 environment can promote research on learning methods for LLMs, helping LLM-based methods better adapt to task scenarios.
Fast and Communication-Efficient Multi-UAV Exploration Via Voronoi Partition on Dynamic Topological Graph
Aug 11, 2024



Abstract:Efficient data transmission and reasonable task allocation are important to improve multi-robot exploration efficiency. However, most communication data types typically contain redundant information and thus require massive communication volume. Moreover, exploration-oriented task allocation is far from trivial and becomes even more challenging for resource-limited unmanned aerial vehicles (UAVs). In this paper, we propose a fast and communication-efficient multi-UAV exploration method for exploring large environments. We first design a multi-robot dynamic topological graph (MR-DTG) consisting of nodes representing the explored and exploring regions and edges connecting nodes. Supported by MR-DTG, our method achieves efficient communication by only transferring the necessary information required by exploration planning. To further improve the exploration efficiency, a hierarchical multi-UAV exploration method is devised using MR-DTG. Specifically, the \emph{graph Voronoi partition} is used to allocate MR-DTG's nodes to the closest UAVs, considering the actual motion cost, thus achieving reasonable task allocation. To our knowledge, this is the first work to address multi-UAV exploration using \emph{graph Voronoi partition}. The proposed method is compared with a state-of-the-art method in simulations. The results show that the proposed method is able to reduce the exploration time and communication volume by up to 38.3\% and 95.5\%, respectively. Finally, the effectiveness of our method is validated in the real-world experiment with 6 UAVs. We will release the source code to benefit the community.
Two-Timescale Optimization Framework for Decentralized Linear-Quadratic Optimal Control
Jun 17, 2024Abstract:This study investigates a decentralized linear-quadratic optimal control problem, and several approximate separable constrained optimization problems are formulated for the first time based on the selection of sparsity promoting functions. First, for the optimization problem with weighted $\ell_1$ sparsity promoting function, a two-timescale algorithm is adopted that is based on the BSUM (Block Successive Upper-bound Minimization) framework and a differential equation solver. Second, a piecewise quadratic sparsity promoting function is introduced, and the induced optimization problem demonstrates an accelerated convergence rate by performing the same two-timescale algorithm. Finally, the optimization problem with $\ell_0$ sparsity promoting function is considered that is nonconvex and discontinuous, and can be approximated by successive coordinatewise convex optimization problems.
6-DoF Robotic Grasping with Transformer
Jan 29, 2023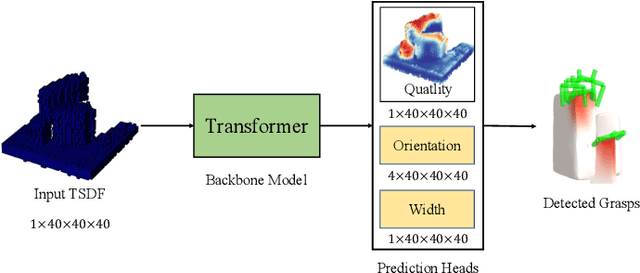
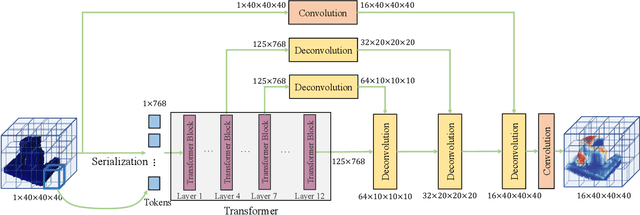
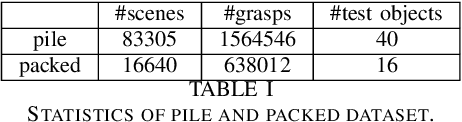
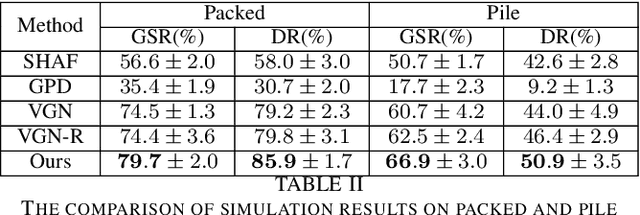
Abstract:Robotic grasping aims to detect graspable points and their corresponding gripper configurations in a particular scene, and is fundamental for robot manipulation. Existing research works have demonstrated the potential of using a transformer model for robotic grasping, which can efficiently learn both global and local features. However, such methods are still limited in grasp detection on a 2D plane. In this paper, we extend a transformer model for 6-Degree-of-Freedom (6-DoF) robotic grasping, which makes it more flexible and suitable for tasks that concern safety. The key designs of our method are a serialization module that turns a 3D voxelized space into a sequence of feature tokens that a transformer model can consume and skip-connections that merge multiscale features effectively. In particular, our method takes a Truncated Signed Distance Function (TSDF) as input. After serializing the TSDF, a transformer model is utilized to encode the sequence, which can obtain a set of aggregated hidden feature vectors through multi-head attention. We then decode the hidden features to obtain per-voxel feature vectors through deconvolution and skip-connections. Voxel feature vectors are then used to regress parameters for executing grasping actions. On a recently proposed pile and packed grasping dataset, we showcase that our transformer-based method can surpass existing methods by about 5% in terms of success rates and declutter rates. We further evaluate the running time and generalization ability to demonstrate the superiority of the proposed method.
CVR-LSE: Compact Vectorization Representation of Local Static Environments for Unmanned Ground Vehicles
Jun 14, 2022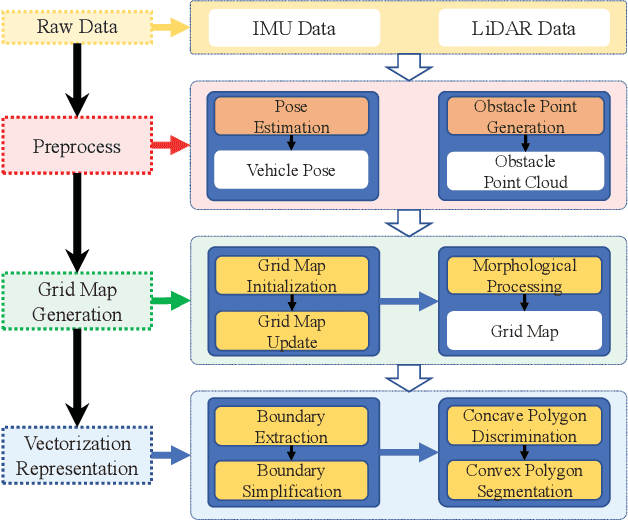
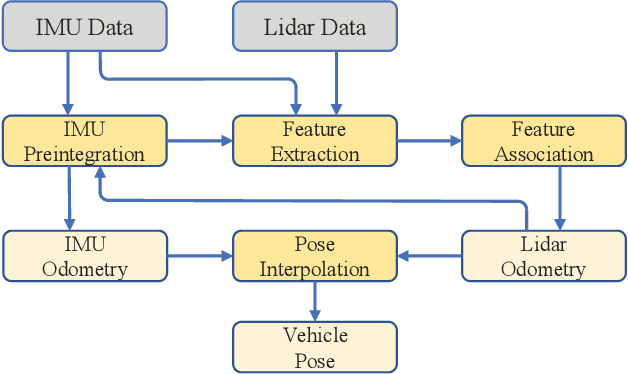
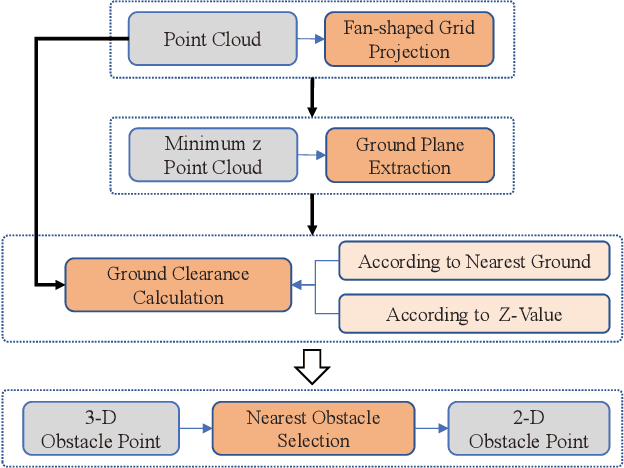
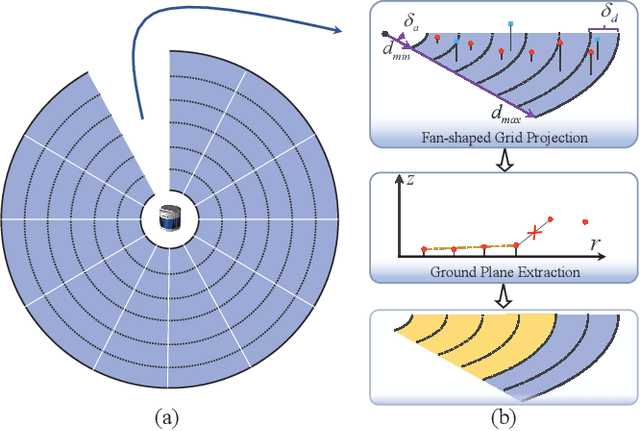
Abstract:According to the requirement of general static obstacle detection, this paper proposes a compact vectorization representation approach of local static environments for unmanned ground vehicles. At first, by fusing the data of LiDAR and IMU, high-frequency pose information is obtained. Then, through the two-dimensional (2D) obstacle points generation, the process of grid map maintenance with a fixed size is proposed. Finally, the local static environment is described via multiple convex polygons, which is realized throungh the double threshold-based boundary simplification and the convex polygon segmentation. Our proposed approach has been applied in a practical driverless project in the park, and the qualitative experimental results on typical scenes verify the effectiveness and robustness. In addition, the quantitative evaluation shows the superior performance on making use of fewer number of points information (decreased by about 60%) to represent the local static environment compared with the traditional grid map-based methods. Furthermore, the performance of running time (15ms) shows that the proposed approach can be used for real-time local static environment perception. The corresponding code can be accessed at https://github.com/ghm0819/cvr_lse.
G$ \mathbf{^2} $VD Planner: An Efficient Motion Planning Approach With Grid-based Generalized Voronoi Diagrams
Feb 01, 2022



Abstract:In this letter, an efficient motion planning approach with grid-based generalized Voronoi diagrams is newly proposed for mobile robots. Different from existing approaches, the novelty of this work is twofold: 1) a new state lattice-based path searching approach is proposed, in which the search space is reduced to a Voronoi corridor to further improve the search efficiency, along with a Voronoi potential field constructed to make the searched path keep a reasonable distance from obstacles to provide sufficient optimization margin for the subsequent path smoothing, and 2) an efficient quadratic programming-based path smoothing approach is presented, wherein the clearance to obstacles is considered in the form of the penalty of the deviation from the safe reference path to improve the path clearance of hard-constrained path smoothing approaches. We validate the efficiency and smoothness of our approach in various challenging simulation scenarios and large-scale outdoor environments. It is shown that the computational efficiency is improved by 17.1% in the path searching stage, and smoothing the path with our approach is 11.86 times faster than a recent gradient-based path smoothing approach. We will release the source code to the robotics community.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge