Graph Neural Networks with Transformer Fusion of Brain Connectivity Dynamics and Tabular Data for Forecasting Future Tobacco Use

Integrating non-Euclidean brain imaging data with Euclidean tabular data, such as clinical and demographic information, poses a substantial challenge for medical imaging analysis, particularly in forecasting future outcomes. While machine learning and deep learning techniques have been applied successfully to cross-sectional classification and prediction tasks, effectively forecasting outcomes in longitudinal imaging studies remains challenging. To address this challenge, we introduce a time-aware graph neural network model with transformer fusion (GNN-TF). This model flexibly integrates both tabular data and dynamic brain connectivity data, leveraging the temporal order of these variables within a coherent framework. By incorporating non-Euclidean and Euclidean sources of information from a longitudinal resting-state fMRI dataset from the National Consortium on Alcohol and Neurodevelopment in Adolescence (NCANDA), the GNN-TF enables a comprehensive analysis that captures critical aspects of longitudinal imaging data. Comparative analyses against a variety of established machine learning and deep learning models demonstrate that GNN-TF outperforms these state-of-the-art methods, delivering superior predictive accuracy for predicting future tobacco usage. The end-to-end, time-aware transformer fusion structure of the proposed GNN-TF model successfully integrates multiple data modalities and leverages temporal dynamics, making it a valuable analytic tool for functional brain imaging studies focused on clinical outcome prediction.

TWLR: Text-Guided Weakly-Supervised Lesion Localization and Severity Regression for Explainable Diabetic Retinopathy Grading

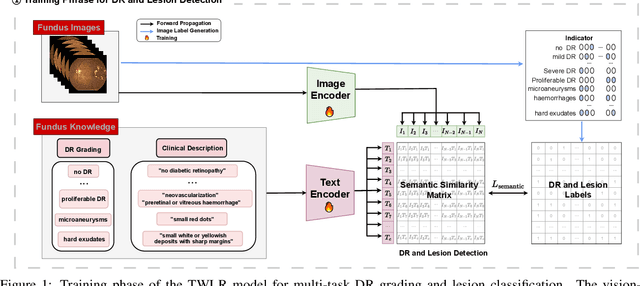
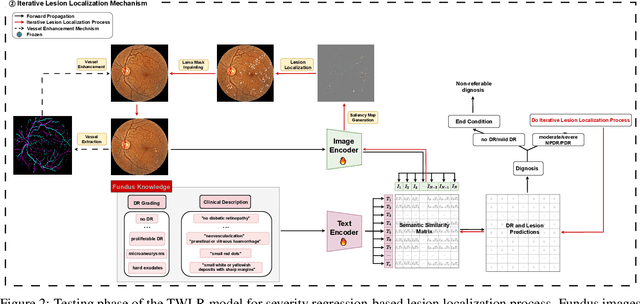
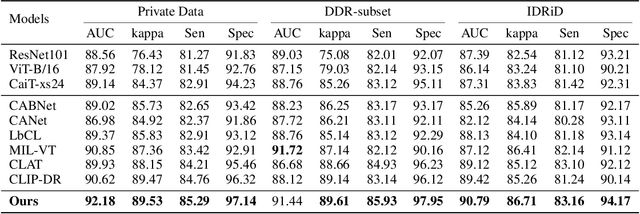
Accurate medical image analysis can greatly assist clinical diagnosis, but its effectiveness relies on high-quality expert annotations Obtaining pixel-level labels for medical images, particularly fundus images, remains costly and time-consuming. Meanwhile, despite the success of deep learning in medical imaging, the lack of interpretability limits its clinical adoption. To address these challenges, we propose TWLR, a two-stage framework for interpretable diabetic retinopathy (DR) assessment. In the first stage, a vision-language model integrates domain-specific ophthalmological knowledge into text embeddings to jointly perform DR grading and lesion classification, effectively linking semantic medical concepts with visual features. The second stage introduces an iterative severity regression framework based on weakly-supervised semantic segmentation. Lesion saliency maps generated through iterative refinement direct a progressive inpainting mechanism that systematically eliminates pathological features, effectively downgrading disease severity toward healthier fundus appearances. Critically, this severity regression approach achieves dual benefits: accurate lesion localization without pixel-level supervision and providing an interpretable visualization of disease-to-healthy transformations. Experimental results on the FGADR, DDR, and a private dataset demonstrate that TWLR achieves competitive performance in both DR classification and lesion segmentation, offering a more explainable and annotation-efficient solution for automated retinal image analysis.

Knowledge Distillation with Adapted Weight

Although large models have shown a strong capacity to solve large-scale problems in many areas including natural language and computer vision, their voluminous parameters are hard to deploy in a real-time system due to computational and energy constraints. Addressing this, knowledge distillation through Teacher-Student architecture offers a sustainable pathway to compress the knowledge of large models into more manageable sizes without significantly compromising performance. To enhance the robustness and interpretability of this framework, it is critical to understand how individual training data impact model performance, which is an area that remains underexplored. We propose the \textbf{Knowledge Distillation with Adaptive Influence Weight (KD-AIF)} framework which leverages influence functions from robust statistics to assign weights to training data, grounded in the four key SAFE principles: Sustainability, Accuracy, Fairness, and Explainability. This novel approach not only optimizes distillation but also increases transparency by revealing the significance of different data. The exploration of various update mechanisms within the KD-AIF framework further elucidates its potential to significantly improve learning efficiency and generalization in student models, marking a step toward more explainable and deployable Large Models. KD-AIF is effective in knowledge distillation while also showing exceptional performance in semi-supervised learning with outperforms existing baselines and methods in multiple benchmarks (CIFAR-100, CIFAR-10-4k, SVHN-1k, and GLUE).

NeutraSum: A Language Model can help a Balanced Media Diet by Neutralizing News Summaries

Media bias in news articles arises from the political polarisation of media outlets, which can reinforce societal stereotypes and beliefs. Reporting on the same event often varies significantly between outlets, reflecting their political leanings through polarised language and focus. Although previous studies have attempted to generate bias-free summaries from multiperspective news articles, they have not effectively addressed the challenge of mitigating inherent media bias. To address this gap, we propose \textbf{NeutraSum}, a novel framework that integrates two neutrality losses to adjust the semantic space of generated summaries, thus minimising media bias. These losses, designed to balance the semantic distances across polarised inputs and ensure alignment with expert-written summaries, guide the generation of neutral and factually rich summaries. To evaluate media bias, we employ the political compass test, which maps political leanings based on economic and social dimensions. Experimental results on the Allsides dataset demonstrate that NeutraSum not only improves summarisation performance but also achieves significant reductions in media bias, offering a promising approach for neutral news summarisation.

Air-Ground Collaborative Robots for Fire and Rescue Missions: Towards Mapping and Navigation Perspective

Air-ground collaborative robots have shown great potential in the field of fire and rescue, which can quickly respond to rescue needs and improve the efficiency of task execution. Mapping and navigation, as the key foundation for air-ground collaborative robots to achieve efficient task execution, have attracted a great deal of attention. This growing interest in collaborative robot mapping and navigation is conducive to improving the intelligence of fire and rescue task execution, but there has been no comprehensive investigation of this field to highlight their strengths. In this paper, we present a systematic review of the ground-to-ground cooperative robots for fire and rescue from a new perspective of mapping and navigation. First, an air-ground collaborative robots framework for fire and rescue missions based on unmanned aerial vehicle (UAV) mapping and unmanned ground vehicle (UGV) navigation is introduced. Then, the research progress of mapping and navigation under this framework is systematically summarized, including UAV mapping, UAV/UGV co-localization, and UGV navigation, with their main achievements and limitations. Based on the needs of fire and rescue missions, the collaborative robots with different numbers of UAVs and UGVs are classified, and their practicality in fire and rescue tasks is elaborated, with a focus on the discussion of their merits and demerits. In addition, the application examples of air-ground collaborative robots in various firefighting and rescue scenarios are given. Finally, this paper emphasizes the current challenges and potential research opportunities, rounding up references for practitioners and researchers willing to engage in this vibrant area of air-ground collaborative robots.

AutoSweep: Recovering 3D Editable Objectsfrom a Single Photograph

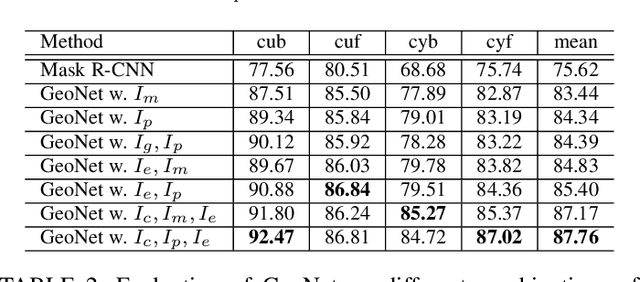
This paper presents a fully automatic framework for extracting editable 3D objects directly from a single photograph. Unlike previous methods which recover either depth maps, point clouds, or mesh surfaces, we aim to recover 3D objects with semantic parts and can be directly edited. We base our work on the assumption that most human-made objects are constituted by parts and these parts can be well represented by generalized primitives. Our work makes an attempt towards recovering two types of primitive-shaped objects, namely, generalized cuboids and generalized cylinders. To this end, we build a novel instance-aware segmentation network for accurate part separation. Our GeoNet outputs a set of smooth part-level masks labeled as profiles and bodies. Then in a key stage, we simultaneously identify profile-body relations and recover 3D parts by sweeping the recognized profile along their body contour and jointly optimize the geometry to align with the recovered masks. Qualitative and quantitative experiments show that our algorithm can recover high quality 3D models and outperforms existing methods in both instance segmentation and 3D reconstruction. The dataset and code of AutoSweep are available at https://chenxin.tech/AutoSweep.html.

Towards 3D Human Shape Recovery Under Clothing

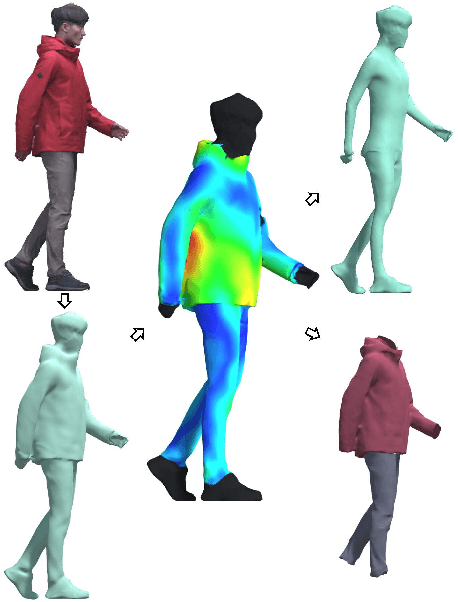
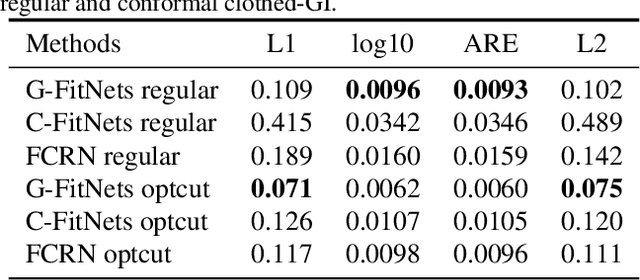
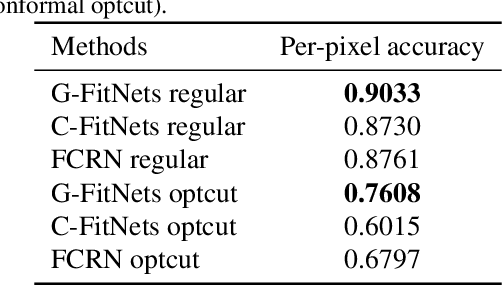
We present a learning-based scheme for robustly and accurately estimating clothing fitness as well as the human shape on clothed 3D human scans. Our approach maps the clothed human geometry to a geometry image that we call clothed-GI. To align clothed-GI under different clothing, we extend the parametric human model and employ skeleton detection and warping for reliable alignment. For each pixel on the clothed-GI, we extract a feature vector including color/texture, position, normal, etc. and train a modified conditional GAN network for per-pixel fitness prediction using a comprehensive 3D clothing. Our technique significantly improves the accuracy of human shape prediction, especially under loose and fitted clothing. We further demonstrate using our results for human/clothing segmentation and virtual clothes fitting at a high visual realism.

Model Assisted Variable Clustering: Minimax-optimal Recovery and Algorithms

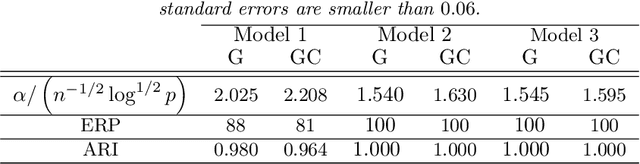
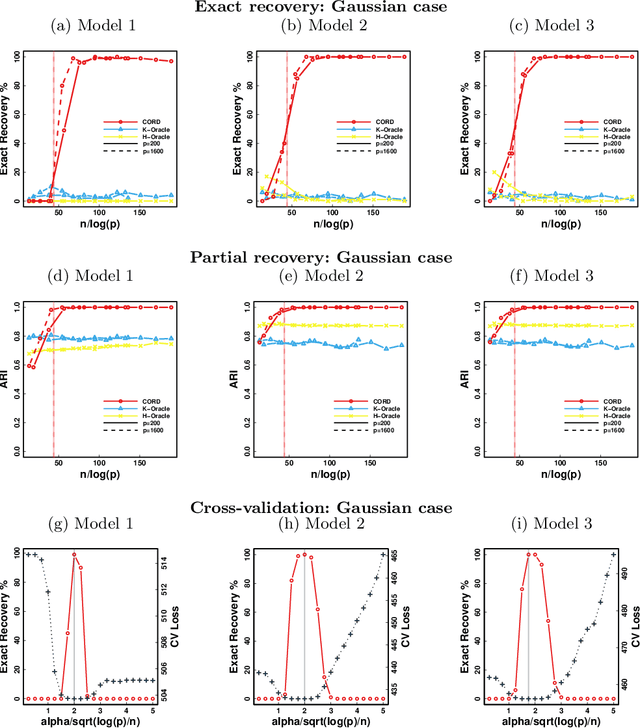
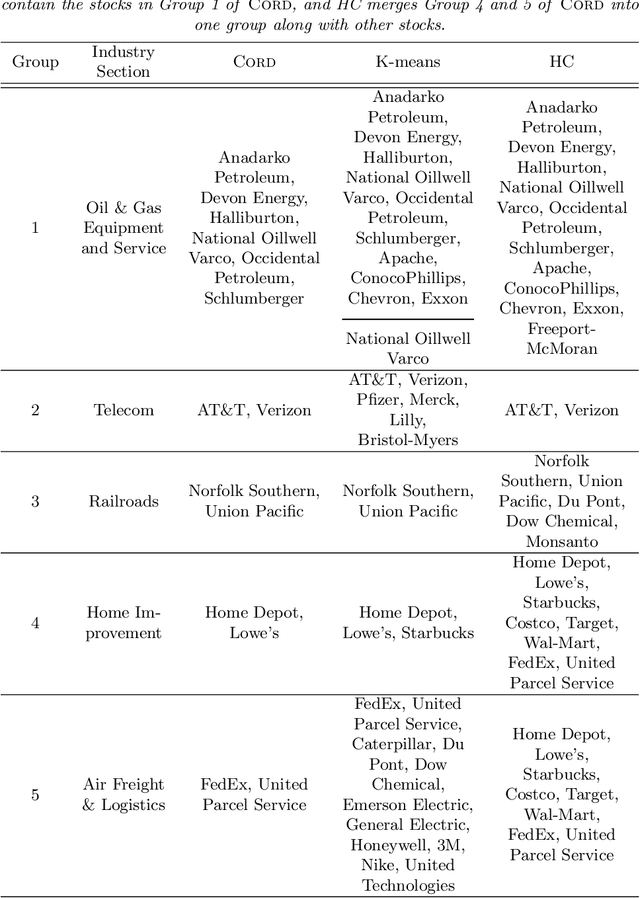
Model-based clustering defines population level clusters relative to a model that embeds notions of similarity. Algorithms tailored to such models yield estimated clusters with a clear statistical interpretation. We take this view here and introduce the class of $G$-block covariance models as a background model for variable clustering. In such models, two variables in a cluster are deemed similar if they have similar associations will all other variables. This can arise, for instance, when groups of variables are noise corrupted versions of the same latent factor. We quantify the difficulty of clustering data generated from a $G$-block covariance model in terms of cluster proximity, measured with respect to two related, but different, cluster separation metrics. We derive minimax cluster separation thresholds, which are the metric values below which no algorithm can recover the model-defined clusters exactly, and show that they are different for the two metrics. We therefore develop two algorithms, COD and PECOK, tailored to G-block covariance models, and study their minimax-optimality with respect to each metric. Of independent interest is the fact that the analysis of the PECOK algorithm, which is based on a corrected convex relaxation of the popular $K$-means algorithm, provides the first statistical analysis of such algorithms for variable clustering. Additionally, we contrast our methods with another popular clustering method, spectral clustering, specialized to variable clustering, and show that ensuring exact cluster recovery via this method requires clusters to have a higher separation, relative to the minimax threshold. Extensive simulation studies, as well as our data analyses, confirm the applicability of our approach.

Granger Mediation Analysis of Multiple Time Series with an Application to fMRI

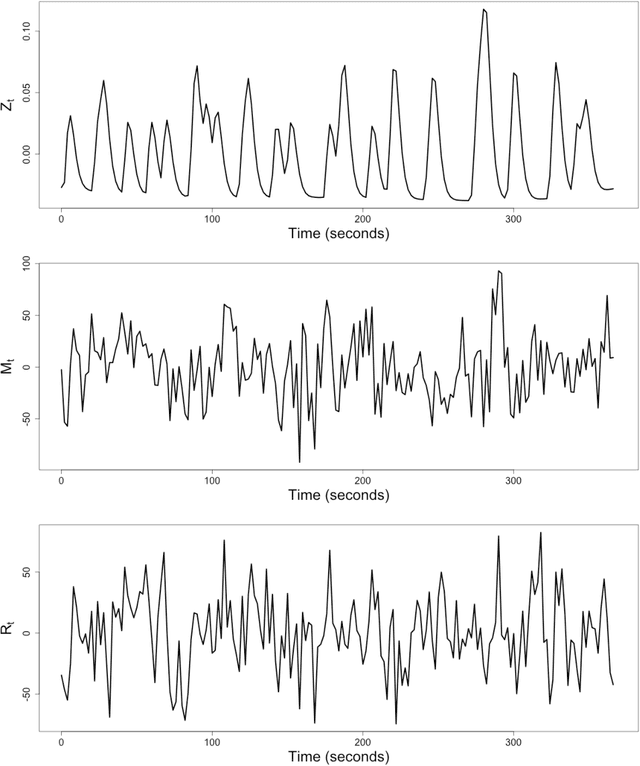
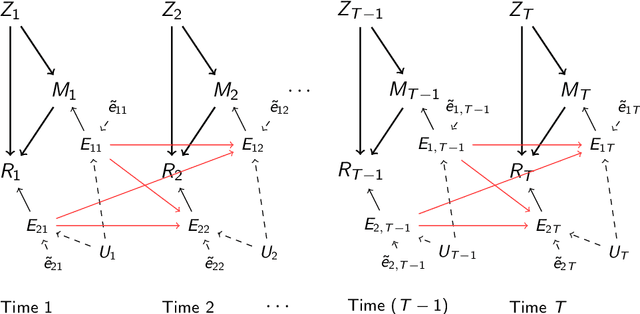
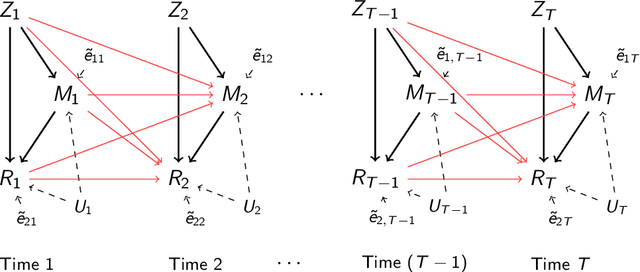
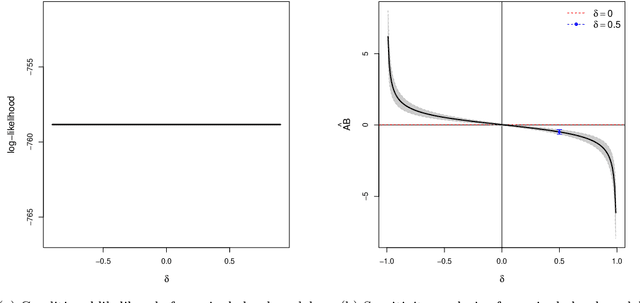
It becomes increasingly popular to perform mediation analysis for complex data from sophisticated experimental studies. In this paper, we present Granger Mediation Analysis (GMA), a new framework for causal mediation analysis of multiple time series. This framework is motivated by a functional magnetic resonance imaging (fMRI) experiment where we are interested in estimating the mediation effects between a randomized stimulus time series and brain activity time series from two brain regions. The stable unit treatment assumption for causal mediation analysis is thus unrealistic for this type of time series data. To address this challenge, our framework integrates two types of models: causal mediation analysis across the variables and vector autoregressive models across the temporal observations. We further extend this framework to handle multilevel data to address individual variability and correlated errors between the mediator and the outcome variables. These models not only provide valid causal mediation for time series data but also model the causal dynamics across time. We show that the modeling parameters in our models are identifiable, and we develop computationally efficient methods to maximize the likelihood-based optimization criteria. Simulation studies show that our method reduces the estimation bias and improve statistical power, compared to existing approaches. On a real fMRI data set, our approach not only infers the causal effects of brain pathways but accurately captures the feedback effect of the outcome region on the mediator region.

Fast and Adaptive Sparse Precision Matrix Estimation in High Dimensions

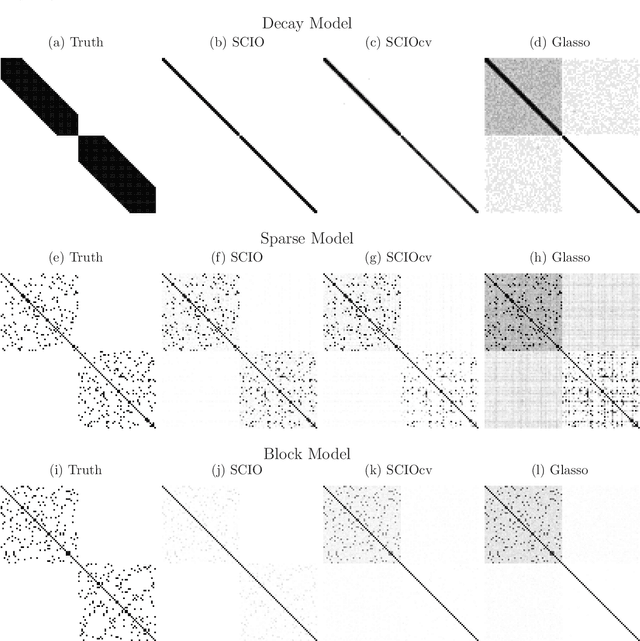
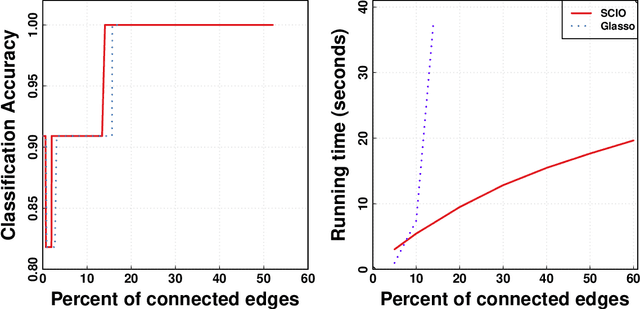
This paper proposes a new method for estimating sparse precision matrices in the high dimensional setting. It has been popular to study fast computation and adaptive procedures for this problem. We propose a novel approach, called Sparse Column-wise Inverse Operator, to address these two issues. We analyze an adaptive procedure based on cross validation, and establish its convergence rate under the Frobenius norm. The convergence rates under other matrix norms are also established. This method also enjoys the advantage of fast computation for large-scale problems, via a coordinate descent algorithm. Numerical merits are illustrated using both simulated and real datasets. In particular, it performs favorably on an HIV brain tissue dataset and an ADHD resting-state fMRI dataset.