Model Assisted Variable Clustering: Minimax-optimal Recovery and Algorithms

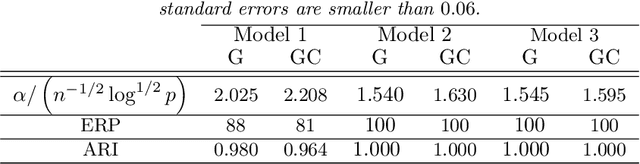
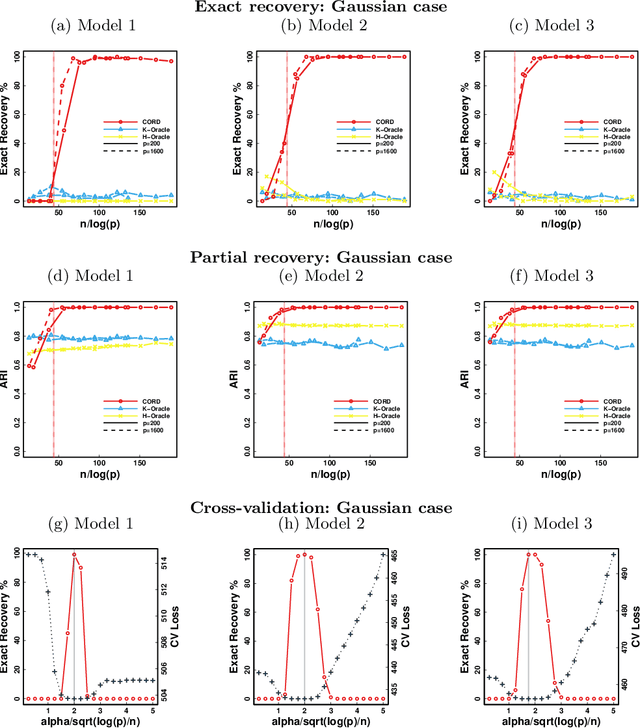
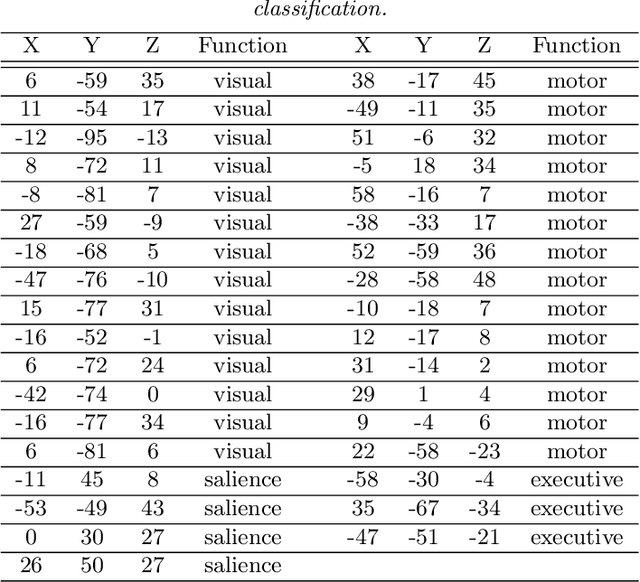
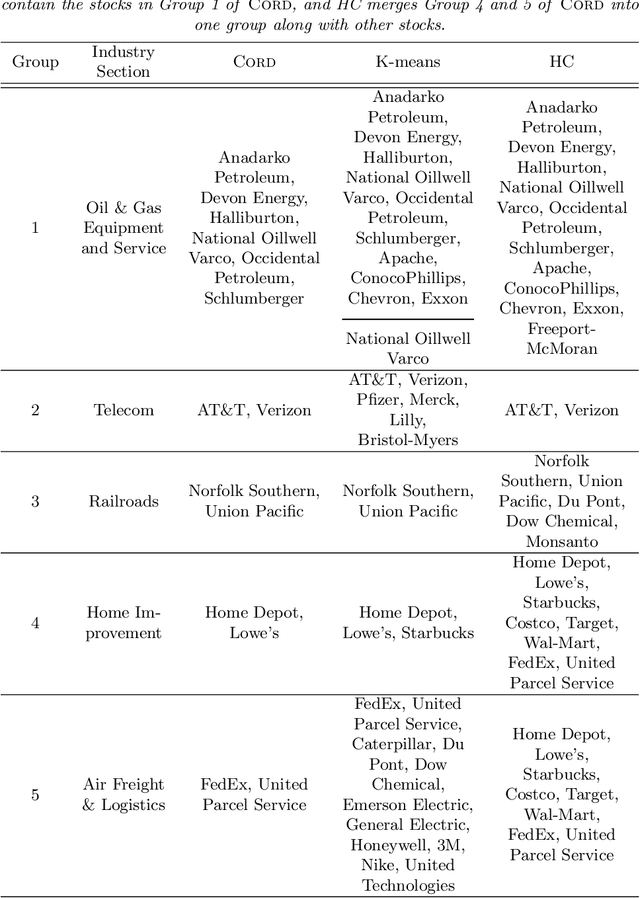
Model-based clustering defines population level clusters relative to a model that embeds notions of similarity. Algorithms tailored to such models yield estimated clusters with a clear statistical interpretation. We take this view here and introduce the class of $G$-block covariance models as a background model for variable clustering. In such models, two variables in a cluster are deemed similar if they have similar associations will all other variables. This can arise, for instance, when groups of variables are noise corrupted versions of the same latent factor. We quantify the difficulty of clustering data generated from a $G$-block covariance model in terms of cluster proximity, measured with respect to two related, but different, cluster separation metrics. We derive minimax cluster separation thresholds, which are the metric values below which no algorithm can recover the model-defined clusters exactly, and show that they are different for the two metrics. We therefore develop two algorithms, COD and PECOK, tailored to G-block covariance models, and study their minimax-optimality with respect to each metric. Of independent interest is the fact that the analysis of the PECOK algorithm, which is based on a corrected convex relaxation of the popular $K$-means algorithm, provides the first statistical analysis of such algorithms for variable clustering. Additionally, we contrast our methods with another popular clustering method, spectral clustering, specialized to variable clustering, and show that ensuring exact cluster recovery via this method requires clusters to have a higher separation, relative to the minimax threshold. Extensive simulation studies, as well as our data analyses, confirm the applicability of our approach.