Pathway Lasso: Estimate and Select Sparse Mediation Pathways with High Dimensional Mediators
Paper and Code
Mar 24, 2016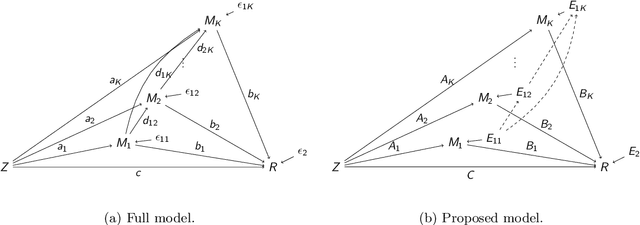
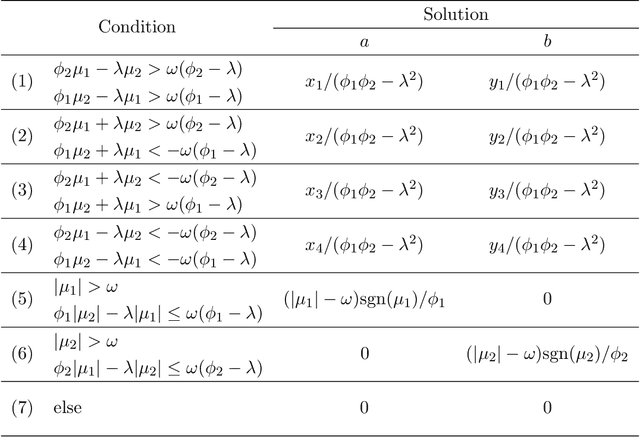
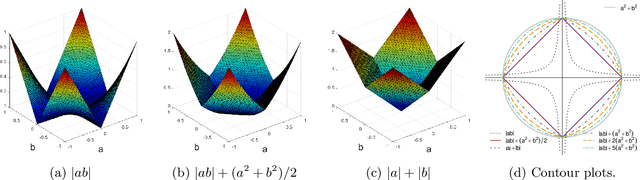
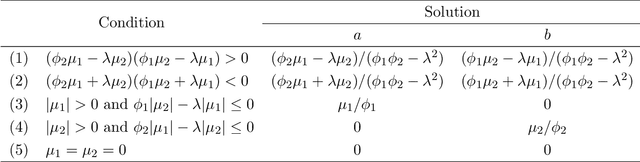
In many scientific studies, it becomes increasingly important to delineate the causal pathways through a large number of mediators, such as genetic and brain mediators. Structural equation modeling (SEM) is a popular technique to estimate the pathway effects, commonly expressed as products of coefficients. However, it becomes unstable to fit such models with high dimensional mediators, especially for a general setting where all the mediators are causally dependent but the exact causal relationships between them are unknown. This paper proposes a sparse mediation model using a regularized SEM approach, where sparsity here means that a small number of mediators have nonzero mediation effects between a treatment and an outcome. To address the model selection challenge, we innovate by introducing a new penalty called Pathway Lasso. This penalty function is a convex relaxation of the non-convex product function, and it enables a computationally tractable optimization criterion to estimate and select many pathway effects simultaneously. We develop a fast ADMM-type algorithm to compute the model parameters, and we show that the iterative updates can be expressed in closed form. On both simulated data and a real fMRI dataset, the proposed approach yields higher pathway selection accuracy and lower estimation bias than other competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge