A Hierarchical Graphical Model for Big Inverse Covariance Estimation with an Application to fMRI
Paper and Code
Apr 07, 2014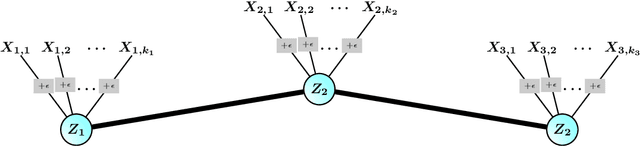
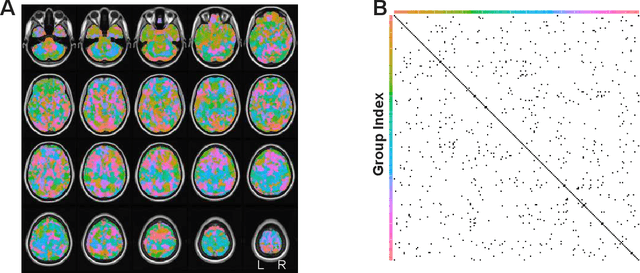
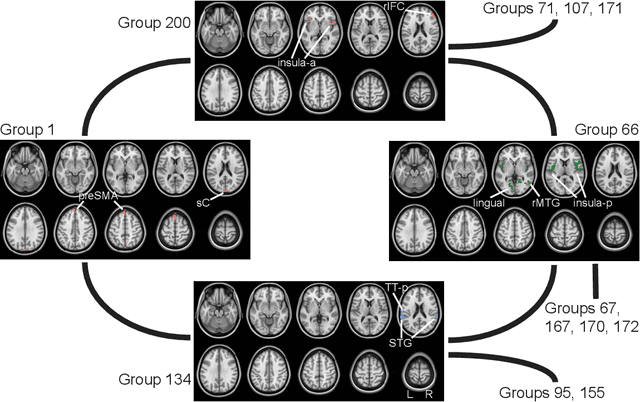
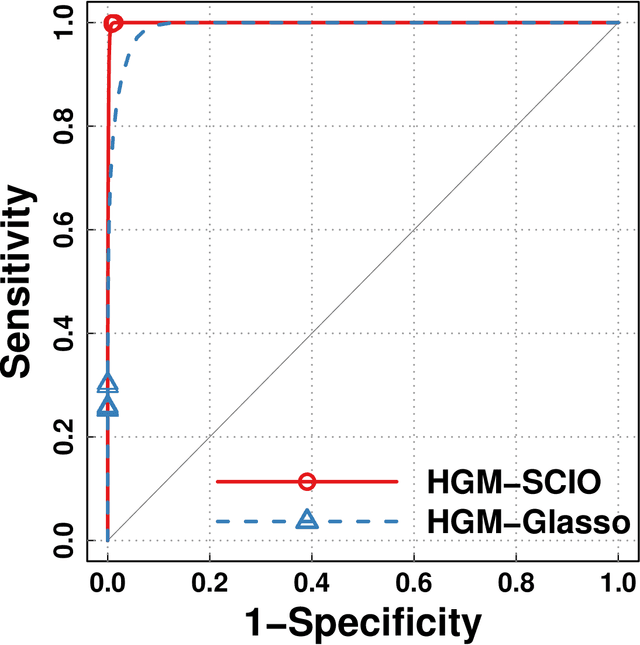
Brain networks has attracted the interests of many neuroscientists. From functional MRI (fMRI) data, statistical tools have been developed to recover brain networks. However, the dimensionality of whole-brain fMRI, usually in hundreds of thousands, challenges the applicability of these methods. We develop a hierarchical graphical model (HGM) to remediate this difficulty. This model introduces a hidden layer of networks based on sparse Gaussian graphical models, and the observed data are sampled from individual network nodes. In fMRI, the network layer models the underlying signals of different brain functional units, and how these units directly interact with each other. The introduction of this hierarchical structure not only provides a formal and interpretable approach, but also enables efficient computation for inferring big networks with hundreds of thousands of nodes. Based on the conditional convexity of our formulation, we develop an alternating update algorithm to compute the HGM model parameters simultaneously. The effectiveness of this approach is demonstrated on simulated data and a real dataset from a stop/go fMRI experiment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge