Diffusion-nested Auto-Regressive Synthesis of Heterogeneous Tabular Data

Autoregressive models are predominant in natural language generation, while their application in tabular data remains underexplored. We posit that this can be attributed to two factors: 1) tabular data contains heterogeneous data type, while the autoregressive model is primarily designed to model discrete-valued data; 2) tabular data is column permutation-invariant, requiring a generation model to generate columns in arbitrary order. This paper proposes a Diffusion-nested Autoregressive model (TabDAR) to address these issues. To enable autoregressive methods for continuous columns, TabDAR employs a diffusion model to parameterize the conditional distribution of continuous features. To ensure arbitrary generation order, TabDAR resorts to masked transformers with bi-directional attention, which simulate various permutations of column order, hence enabling it to learn the conditional distribution of a target column given an arbitrary combination of other columns. These designs enable TabDAR to not only freely handle heterogeneous tabular data but also support convenient and flexible unconditional/conditional sampling. We conduct extensive experiments on ten datasets with distinct properties, and the proposed TabDAR outperforms previous state-of-the-art methods by 18% to 45% on eight metrics across three distinct aspects.

Neural Message Passing Induced by Energy-Constrained Diffusion

Learning representations for structured data with certain geometries (observed or unobserved) is a fundamental challenge, wherein message passing neural networks (MPNNs) have become a de facto class of model solutions. In this paper, we propose an energy-constrained diffusion model as a principled interpretable framework for understanding the mechanism of MPNNs and navigating novel architectural designs. The model, inspired by physical systems, combines the inductive bias of diffusion on manifolds with layer-wise constraints of energy minimization. As shown by our analysis, the diffusion operators have a one-to-one correspondence with the energy functions implicitly descended by the diffusion process, and the finite-difference iteration for solving the energy-constrained diffusion system induces the propagation layers of various types of MPNNs operated on observed or latent structures. On top of these findings, we devise a new class of neural message passing models, dubbed as diffusion-inspired Transformers, whose global attention layers are induced by the principled energy-constrained diffusion. Across diverse datasets ranging from real-world networks to images and physical particles, we show that the new model can yield promising performance for cases where the data structures are observed (as a graph), partially observed or completely unobserved.

SGFormer: Single-Layer Graph Transformers with Approximation-Free Linear Complexity

Learning representations on large graphs is a long-standing challenge due to the inter-dependence nature. Transformers recently have shown promising performance on small graphs thanks to its global attention for capturing all-pair interactions beyond observed structures. Existing approaches tend to inherit the spirit of Transformers in language and vision tasks, and embrace complicated architectures by stacking deep attention-based propagation layers. In this paper, we attempt to evaluate the necessity of adopting multi-layer attentions in Transformers on graphs, which considerably restricts the efficiency. Specifically, we analyze a generic hybrid propagation layer, comprised of all-pair attention and graph-based propagation, and show that multi-layer propagation can be reduced to one-layer propagation, with the same capability for representation learning. It suggests a new technical path for building powerful and efficient Transformers on graphs, particularly through simplifying model architectures without sacrificing expressiveness. As exemplified by this work, we propose a Simplified Single-layer Graph Transformers (SGFormer), whose main component is a single-layer global attention that scales linearly w.r.t. graph sizes and requires none of any approximation for accommodating all-pair interactions. Empirically, SGFormer successfully scales to the web-scale graph ogbn-papers100M, yielding orders-of-magnitude inference acceleration over peer Transformers on medium-sized graphs, and demonstrates competitiveness with limited labeled data.

GeoMix: Towards Geometry-Aware Data Augmentation

Mixup has shown considerable success in mitigating the challenges posed by limited labeled data in image classification. By synthesizing samples through the interpolation of features and labels, Mixup effectively addresses the issue of data scarcity. However, it has rarely been explored in graph learning tasks due to the irregularity and connectivity of graph data. Specifically, in node classification tasks, Mixup presents a challenge in creating connections for synthetic data. In this paper, we propose Geometric Mixup (GeoMix), a simple and interpretable Mixup approach leveraging in-place graph editing. It effectively utilizes geometry information to interpolate features and labels with those from the nearby neighborhood, generating synthetic nodes and establishing connections for them. We conduct theoretical analysis to elucidate the rationale behind employing geometry information for node Mixup, emphasizing the significance of locality enhancement-a critical aspect of our method's design. Extensive experiments demonstrate that our lightweight Geometric Mixup achieves state-of-the-art results on a wide variety of standard datasets with limited labeled data. Furthermore, it significantly improves the generalization capability of underlying GNNs across various challenging out-of-distribution generalization tasks. Our code is available at https://github.com/WtaoZhao/geomix.

Learning Divergence Fields for Shift-Robust Graph Representations

Real-world data generation often involves certain geometries (e.g., graphs) that induce instance-level interdependence. This characteristic makes the generalization of learning models more difficult due to the intricate interdependent patterns that impact data-generative distributions and can vary from training to testing. In this work, we propose a geometric diffusion model with learnable divergence fields for the challenging generalization problem with interdependent data. We generalize the diffusion equation with stochastic diffusivity at each time step, which aims to capture the multi-faceted information flows among interdependent data. Furthermore, we derive a new learning objective through causal inference, which can guide the model to learn generalizable patterns of interdependence that are insensitive across domains. Regarding practical implementation, we introduce three model instantiations that can be considered as the generalized versions of GCN, GAT, and Transformers, respectively, which possess advanced robustness against distribution shifts. We demonstrate their promising efficacy for out-of-distribution generalization on diverse real-world datasets.

Graph Out-of-Distribution Generalization via Causal Intervention

Out-of-distribution (OOD) generalization has gained increasing attentions for learning on graphs, as graph neural networks (GNNs) often exhibit performance degradation with distribution shifts. The challenge is that distribution shifts on graphs involve intricate interconnections between nodes, and the environment labels are often absent in data. In this paper, we adopt a bottom-up data-generative perspective and reveal a key observation through causal analysis: the crux of GNNs' failure in OOD generalization lies in the latent confounding bias from the environment. The latter misguides the model to leverage environment-sensitive correlations between ego-graph features and target nodes' labels, resulting in undesirable generalization on new unseen nodes. Built upon this analysis, we introduce a conceptually simple yet principled approach for training robust GNNs under node-level distribution shifts, without prior knowledge of environment labels. Our method resorts to a new learning objective derived from causal inference that coordinates an environment estimator and a mixture-of-expert GNN predictor. The new approach can counteract the confounding bias in training data and facilitate learning generalizable predictive relations. Extensive experiment demonstrates that our model can effectively enhance generalization with various types of distribution shifts and yield up to 27.4\% accuracy improvement over state-of-the-arts on graph OOD generalization benchmarks. Source codes are available at https://github.com/fannie1208/CaNet.

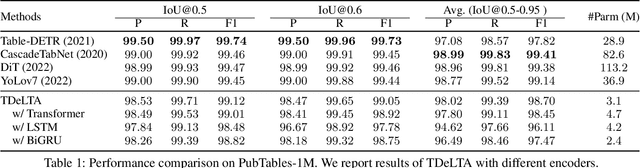
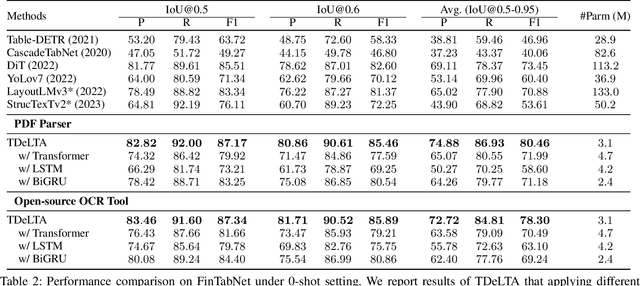
TDeLTA: A Light-weight and Robust Table Detection Method based on Learning Text Arrangement

The diversity of tables makes table detection a great challenge, leading to existing models becoming more tedious and complex. Despite achieving high performance, they often overfit to the table style in training set, and suffer from significant performance degradation when encountering out-of-distribution tables in other domains. To tackle this problem, we start from the essence of the table, which is a set of text arranged in rows and columns. Based on this, we propose a novel, light-weighted and robust Table Detection method based on Learning Text Arrangement, namely TDeLTA. TDeLTA takes the text blocks as input, and then models the arrangement of them with a sequential encoder and an attention module. To locate the tables precisely, we design a text-classification task, classifying the text blocks into 4 categories according to their semantic roles in the tables. Experiments are conducted on both the text blocks parsed from PDF and extracted by open-source OCR tools, respectively. Compared to several state-of-the-art methods, TDeLTA achieves competitive results with only 3.1M model parameters on the large-scale public datasets. Moreover, when faced with the cross-domain data under the 0-shot setting, TDeLTA outperforms baselines by a large margin of nearly 7%, which shows the strong robustness and transferability of the proposed model.

Rethinking Cross-Domain Sequential Recommendation under Open-World Assumptions

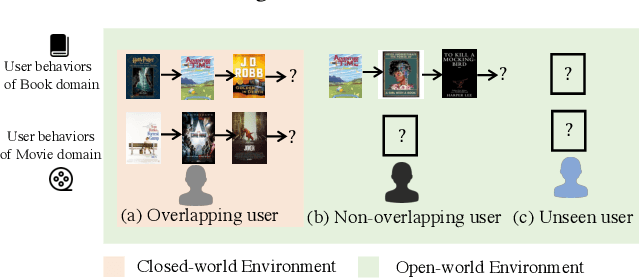
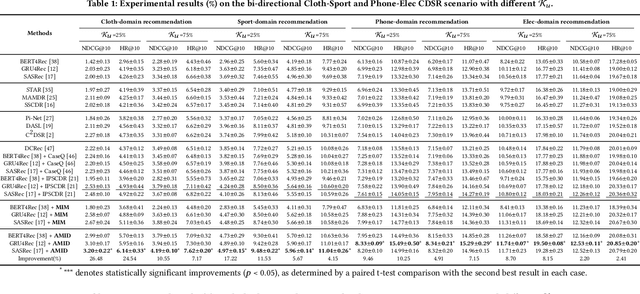
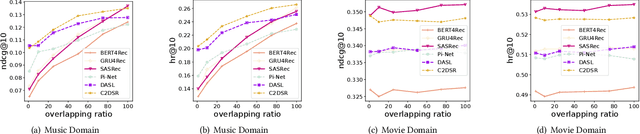
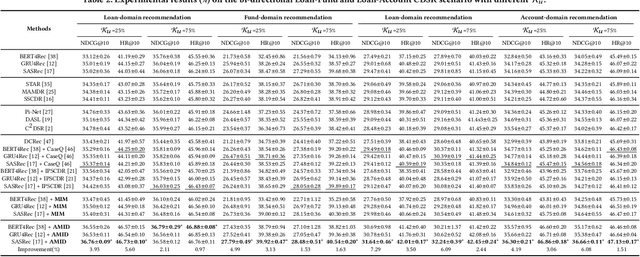
Cross-Domain Sequential Recommendation (CDSR) methods aim to tackle the data sparsity and cold-start problems present in Single-Domain Sequential Recommendation (SDSR). Existing CDSR works design their elaborate structures relying on overlapping users to propagate the cross-domain information. However, current CDSR methods make closed-world assumptions, assuming fully overlapping users across multiple domains and that the data distribution remains unchanged from the training environment to the test environment. As a result, these methods typically result in lower performance on online real-world platforms due to the data distribution shifts. To address these challenges under open-world assumptions, we design an \textbf{A}daptive \textbf{M}ulti-\textbf{I}nterest \textbf{D}ebiasing framework for cross-domain sequential recommendation (\textbf{AMID}), which consists of a multi-interest information module (\textbf{MIM}) and a doubly robust estimator (\textbf{DRE}). Our framework is adaptive for open-world environments and can improve the model of most off-the-shelf single-domain sequential backbone models for CDSR. Our MIM establishes interest groups that consider both overlapping and non-overlapping users, allowing us to effectively explore user intent and explicit interest. To alleviate biases across multiple domains, we developed the DRE for the CDSR methods. We also provide a theoretical analysis that demonstrates the superiority of our proposed estimator in terms of bias and tail bound, compared to the IPS estimator used in previous work.

Advective Diffusion Transformers for Topological Generalization in Graph Learning

Graph diffusion equations are intimately related to graph neural networks (GNNs) and have recently attracted attention as a principled framework for analyzing GNN dynamics, formalizing their expressive power, and justifying architectural choices. One key open questions in graph learning is the generalization capabilities of GNNs. A major limitation of current approaches hinges on the assumption that the graph topologies in the training and test sets come from the same distribution. In this paper, we make steps towards understanding the generalization of GNNs by exploring how graph diffusion equations extrapolate and generalize in the presence of varying graph topologies. We first show deficiencies in the generalization capability of existing models built upon local diffusion on graphs, stemming from the exponential sensitivity to topology variation. Our subsequent analysis reveals the promise of non-local diffusion, which advocates for feature propagation over fully-connected latent graphs, under the assumption of a specific data-generating condition. In addition to these findings, we propose a novel graph encoder backbone, Advective Diffusion Transformer (ADiT), inspired by advective graph diffusion equations that have a closed-form solution backed up with theoretical guarantees of desired generalization under topological distribution shifts. The new model, functioning as a versatile graph Transformer, demonstrates superior performance across a wide range of graph learning tasks.

How Graph Neural Networks Learn: Lessons from Training Dynamics in Function Space

A long-standing goal in deep learning has been to characterize the learning behavior of black-box models in a more interpretable manner. For graph neural networks (GNNs), considerable advances have been made in formalizing what functions they can represent, however it remains less clear whether and how GNNs learn desired functions during the optimization process. To fill this critical gap, we study the learning dynamics of GNNs in function space via the analytic framework of overparameterization. In particular, we find that the seemingly complicated training process of GNNs can be re-cast into a more familiar label propagation framework, due to the graph inductive bias implicit in this process. From this vantage point, we provide explanations for why the learned GNN functions successfully generalize and for their pathological behavior on heterophilic graphs, which are consistent with observations. Practically, sparsifying and implementing the learning dynamics lead to a minimalist semi-supervised learning algorithm with the efficiency of classic algorithms and the effectiveness of modern GNNs.