Earth Observation Satellite Scheduling with Graph Neural Networks

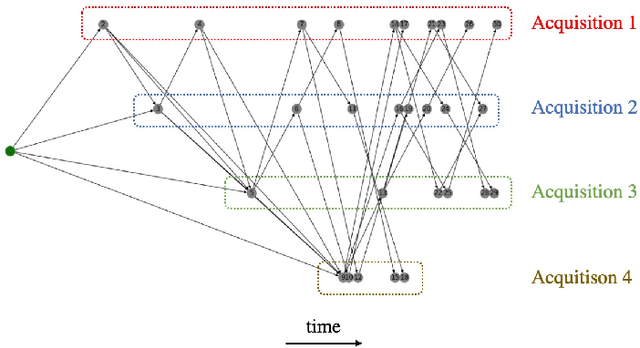
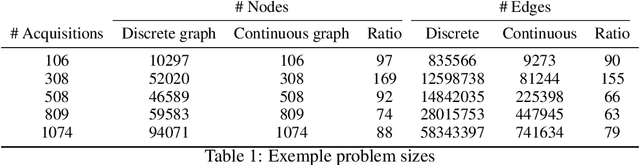
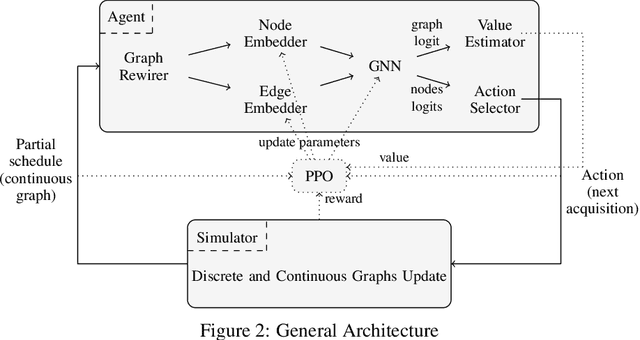
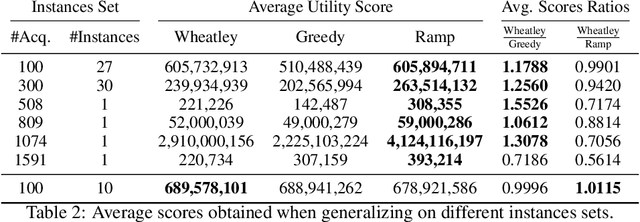
The Earth Observation Satellite Planning (EOSP) is a difficult optimization problem with considerable practical interest. A set of requested observations must be scheduled on an agile Earth observation satellite while respecting constraints on their visibility window, as well as maneuver constraints that impose varying delays between successive observations. In addition, the problem is largely oversubscribed: there are much more candidate observations than what can possibly be achieved. Therefore, one must select the set of observations that will be performed while maximizing their weighted cumulative benefit, and propose a feasible schedule for these observations. As previous work mostly focused on heuristic and iterative search algorithms, this paper presents a new technique for selecting and scheduling observations based on Graph Neural Networks (GNNs) and Deep Reinforcement Learning (DRL). GNNs are used to extract relevant information from the graphs representing instances of the EOSP, and DRL drives the search for optimal schedules. Our simulations show that it is able to learn on small problem instances and generalize to larger real-world instances, with very competitive performance compared to traditional approaches.

Learning to Cooperate via Policy Search

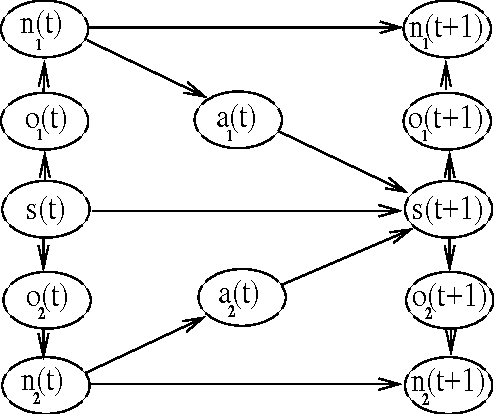
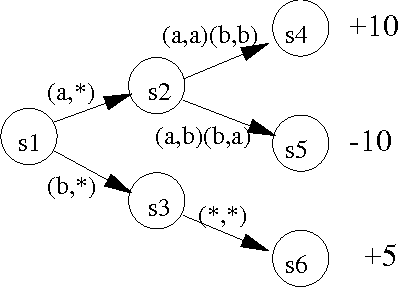
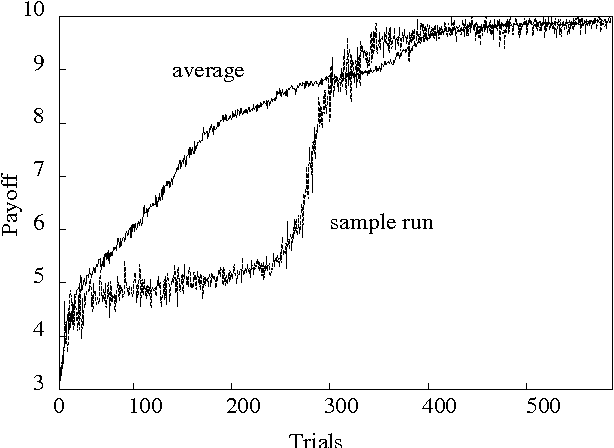
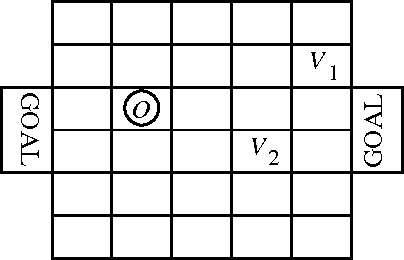
Cooperative games are those in which both agents share the same payoff structure. Value-based reinforcement-learning algorithms, such as variants of Q-learning, have been applied to learning cooperative games, but they only apply when the game state is completely observable to both agents. Policy search methods are a reasonable alternative to value-based methods for partially observable environments. In this paper, we provide a gradient-based distributed policy-search method for cooperative games and compare the notion of local optimum to that of Nash equilibrium. We demonstrate the effectiveness of this method experimentally in a small, partially observable simulated soccer domain.

A Heuristic Search Approach to Planning with Continuous Resources in Stochastic Domains

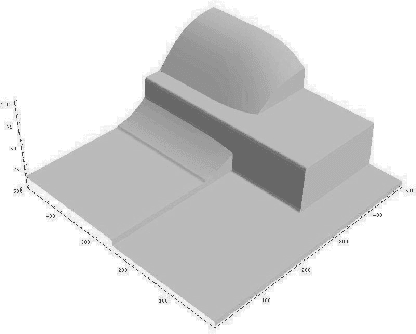
We consider the problem of optimal planning in stochastic domains with resource constraints, where the resources are continuous and the choice of action at each step depends on resource availability. We introduce the HAO* algorithm, a generalization of the AO* algorithm that performs search in a hybrid state space that is modeled using both discrete and continuous state variables, where the continuous variables represent monotonic resources. Like other heuristic search algorithms, HAO* leverages knowledge of the start state and an admissible heuristic to focus computational effort on those parts of the state space that could be reached from the start state by following an optimal policy. We show that this approach is especially effective when resource constraints limit how much of the state space is reachable. Experimental results demonstrate its effectiveness in the domain that motivates our research: automated planning for planetary exploration rovers.

Hierarchical Solution of Markov Decision Processes using Macro-actions

We investigate the use of temporally abstract actions, or macro-actions, in the solution of Markov decision processes. Unlike current models that combine both primitive actions and macro-actions and leave the state space unchanged, we propose a hierarchical model (using an abstract MDP) that works with macro-actions only, and that significantly reduces the size of the state space. This is achieved by treating macroactions as local policies that act in certain regions of state space, and by restricting states in the abstract MDP to those at the boundaries of regions. The abstract MDP approximates the original and can be solved more efficiently. We discuss several ways in which macro-actions can be generated to ensure good solution quality. Finally, we consider ways in which macro-actions can be reused to solve multiple, related MDPs; and we show that this can justify the computational overhead of macro-action generation.

Learning Finite-State Controllers for Partially Observable Environments

Reactive (memoryless) policies are sufficient in completely observable Markov decision processes (MDPs), but some kind of memory is usually necessary for optimal control of a partially observable MDP. Policies with finite memory can be represented as finite-state automata. In this paper, we extend Baird and Moore's VAPS algorithm to the problem of learning general finite-state automata. Because it performs stochastic gradient descent, this algorithm can be shown to converge to a locally optimal finite-state controller. We provide the details of the algorithm and then consider the question of under what conditions stochastic gradient descent will outperform exact gradient descent. We conclude with empirical results comparing the performance of stochastic and exact gradient descent, and showing the ability of our algorithm to extract the useful information contained in the sequence of past observations to compensate for the lack of observability at each time-step.

Solving POMDPs by Searching the Space of Finite Policies

Solving partially observable Markov decision processes (POMDPs) is highly intractable in general, at least in part because the optimal policy may be infinitely large. In this paper, we explore the problem of finding the optimal policy from a restricted set of policies, represented as finite state automata of a given size. This problem is also intractable, but we show that the complexity can be greatly reduced when the POMDP and/or policy are further constrained. We demonstrate good empirical results with a branch-and-bound method for finding globally optimal deterministic policies, and a gradient-ascent method for finding locally optimal stochastic policies.

Planning under Continuous Time and Resource Uncertainty: A Challenge for AI

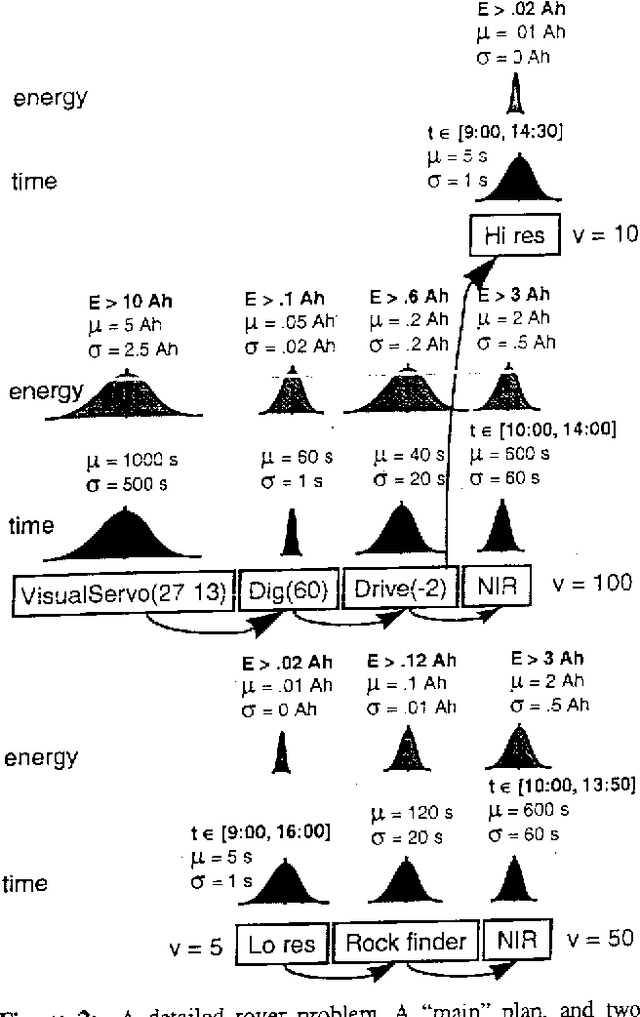
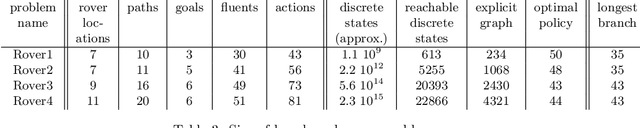
We outline a class of problems, typical of Mars rover operations, that are problematic for current methods of planning under uncertainty. The existing methods fail because they suffer from one or more of the following limitations: 1) they rely on very simple models of actions and time, 2) they assume that uncertainty is manifested in discrete action outcomes, 3) they are only practical for very small problems. For many real world problems, these assumptions fail to hold. In particular, when planning the activities for a Mars rover, none of the above assumptions is valid: 1) actions can be concurrent and have differing durations, 2) there is uncertainty concerning action durations and consumption of continuous resources like power, and 3) typical daily plans involve on the order of a hundred actions. This class of problems may be of particular interest to the UAI community because both classical and decision-theoretic planning techniques may be useful in solving it. We describe the rover problem, discuss previous work on planning under uncertainty, and present a detailed, but very small, example illustrating some of the difficulties of finding good plans.

Optimal Limited Contingency Planning

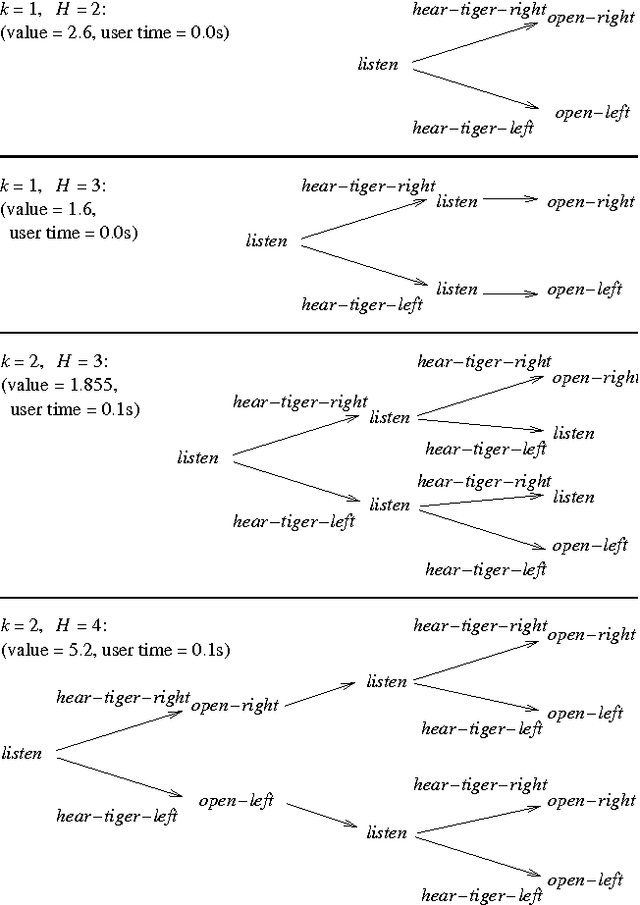
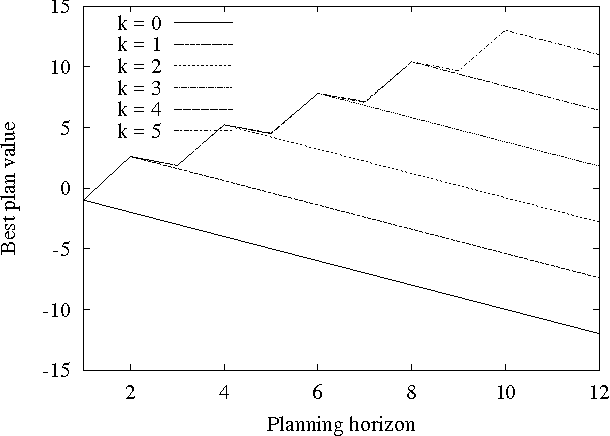
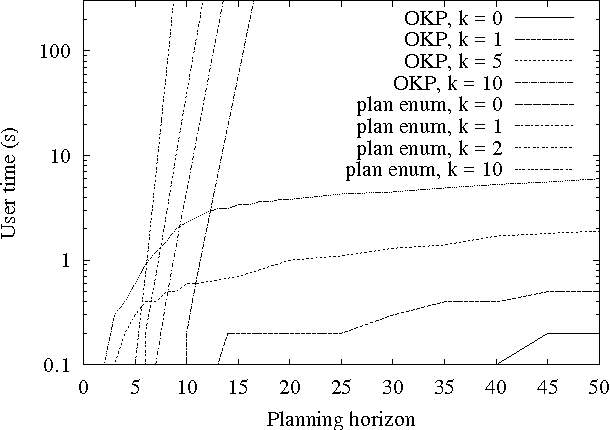
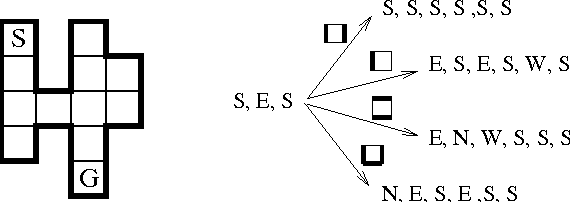
For a given problem, the optimal Markov policy can be considerred as a conditional or contingent plan containing a (potentially large) number of branches. Unfortunately, there are applications where it is desirable to strictly limit the number of decision points and branches in a plan. For example, it may be that plans must later undergo more detailed simulation to verify correctness and safety, or that they must be simple enough to be understood and analyzed by humans. As a result, it may be necessary to limit consideration to plans with only a small number of branches. This raises the question of how one goes about finding optimal plans containing only a limited number of branches. In this paper, we present an any-time algorithm for optimal k-contingency planning (OKP). It is the first optimal algorithm for limited contingency planning that is not an explicit enumeration of possible contingent plans. By modelling the problem as a Partially Observable Markov Decision Process, it implements the Bellman optimality principle and prunes the solution space. We present experimental results of applying this algorithm to some simple test cases.

Dynamic Programming for Structured Continuous Markov Decision Problems

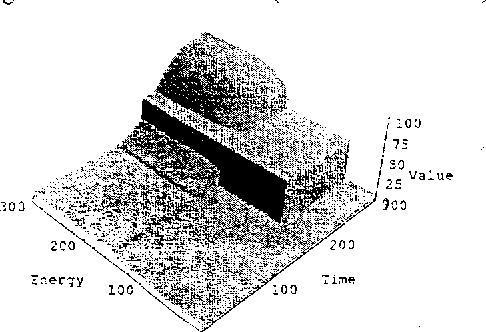
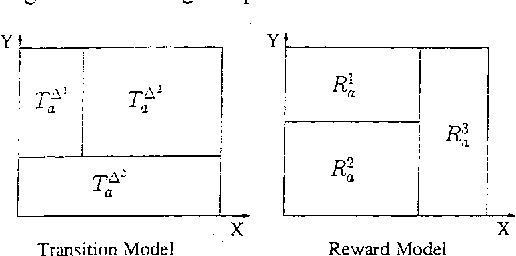
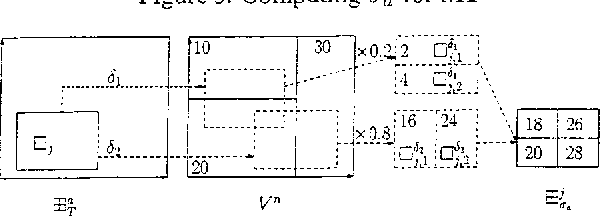
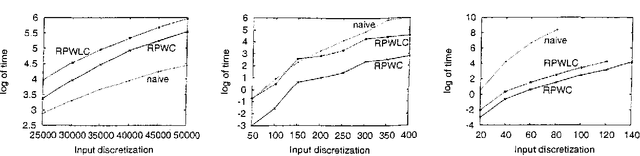
We describe an approach for exploiting structure in Markov Decision Processes with continuous state variables. At each step of the dynamic programming, the state space is dynamically partitioned into regions where the value function is the same throughout the region. We first describe the algorithm for piecewise constant representations. We then extend it to piecewise linear representations, using techniques from POMDPs to represent and reason about linear surfaces efficiently. We show that for complex, structured problems, our approach exploits the natural structure so that optimal solutions can be computed efficiently.

Learning Policies with External Memory

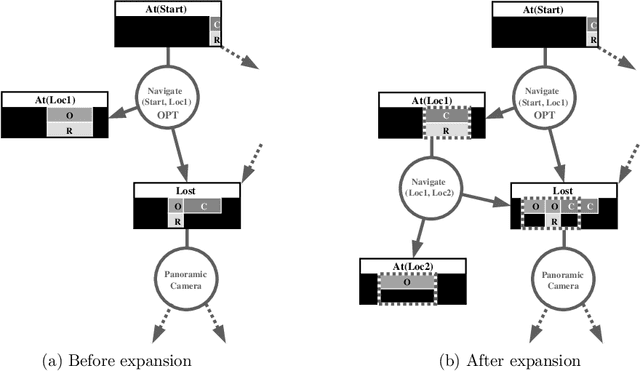
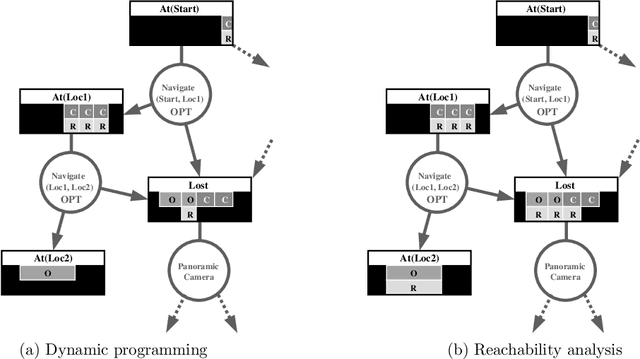
In order for an agent to perform well in partially observable domains, it is usually necessary for actions to depend on the history of observations. In this paper, we explore a {\it stigmergic} approach, in which the agent's actions include the ability to set and clear bits in an external memory, and the external memory is included as part of the input to the agent. In this case, we need to learn a reactive policy in a highly non-Markovian domain. We explore two algorithms: SARSA(\lambda), which has had empirical success in partially observable domains, and VAPS, a new algorithm due to Baird and Moore, with convergence guarantees in partially observable domains. We compare the performance of these two algorithms on benchmark problems.