Symbolic Generalization for On-line Planning

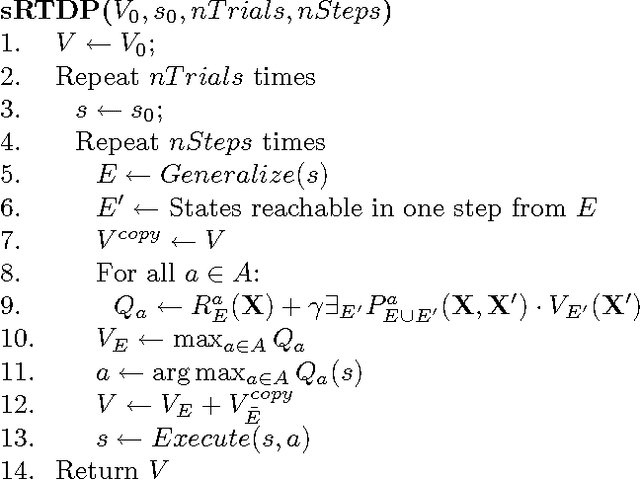
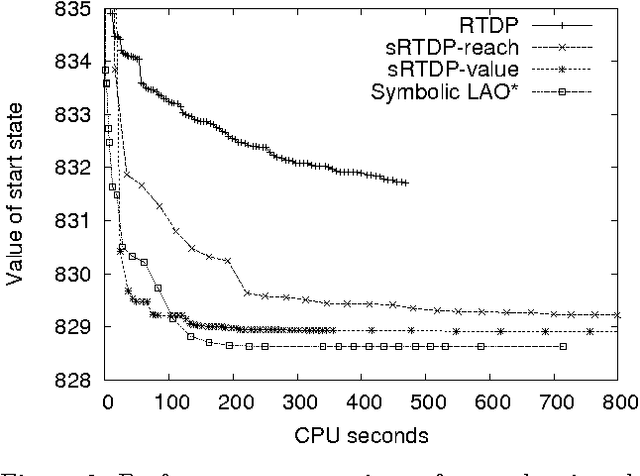
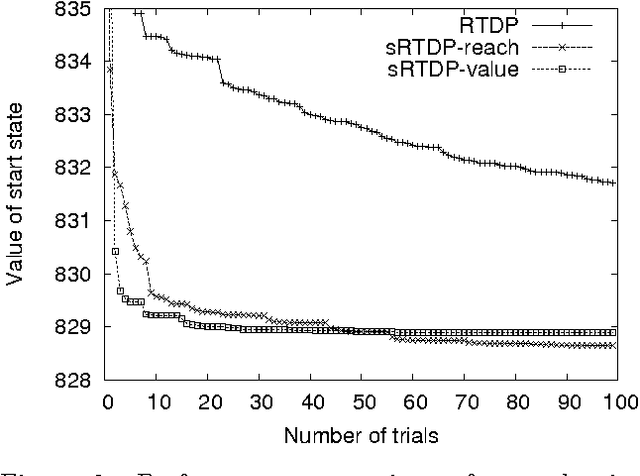
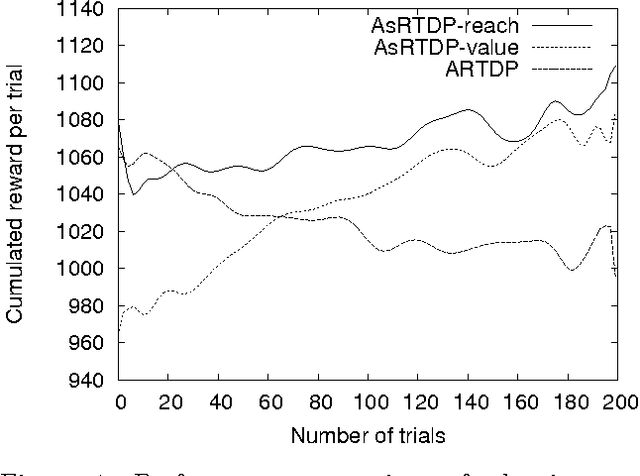
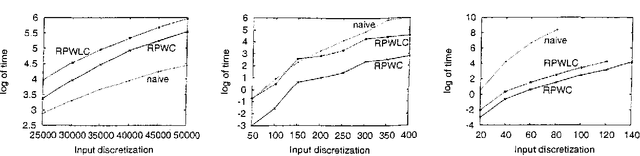
Symbolic representations have been used successfully in off-line planning algorithms for Markov decision processes. We show that they can also improve the performance of on-line planners. In addition to reducing computation time, symbolic generalization can reduce the amount of costly real-world interactions required for convergence. We introduce Symbolic Real-Time Dynamic Programming (or sRTDP), an extension of RTDP. After each step of on-line interaction with an environment, sRTDP uses symbolic model-checking techniques to generalizes its experience by updating a group of states rather than a single state. We examine two heuristic approaches to dynamic grouping of states and show that they accelerate the planning process significantly in terms of both CPU time and the number of steps of interaction with the environment.

Region-Based Incremental Pruning for POMDPs

We present a major improvement to the incremental pruning algorithm for solving partially observable Markov decision processes. Our technique targets the cross-sum step of the dynamic programming (DP) update, a key source of complexity in POMDP algorithms. Instead of reasoning about the whole belief space when pruning the cross-sums, our algorithm divides the belief space into smaller regions and performs independent pruning in each region. We evaluate the benefits of the new technique both analytically and experimentally, and show that it produces very significant performance gains. The results contribute to the scalability of POMDP algorithms to domains that cannot be handled by the best existing techniques.

Dynamic Programming for Structured Continuous Markov Decision Problems

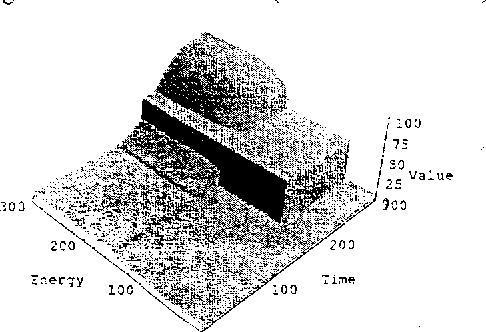
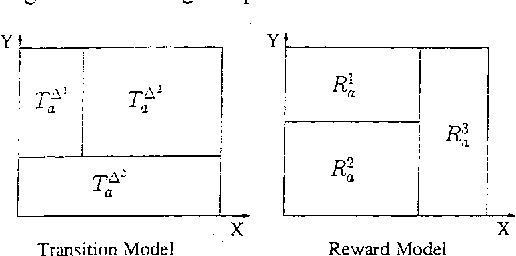
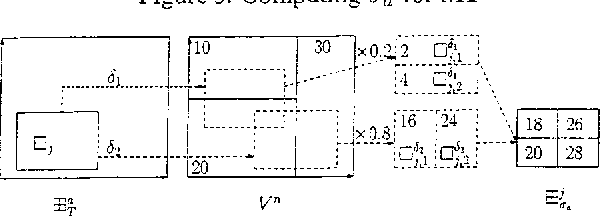
We describe an approach for exploiting structure in Markov Decision Processes with continuous state variables. At each step of the dynamic programming, the state space is dynamically partitioned into regions where the value function is the same throughout the region. We first describe the algorithm for piecewise constant representations. We then extend it to piecewise linear representations, using techniques from POMDPs to represent and reason about linear surfaces efficiently. We show that for complex, structured problems, our approach exploits the natural structure so that optimal solutions can be computed efficiently.