Policy Iteration for Decentralized Control of Markov Decision Processes

Coordination of distributed agents is required for problems arising in many areas, including multi-robot systems, networking and e-commerce. As a formal framework for such problems, we use the decentralized partially observable Markov decision process (DEC-POMDP). Though much work has been done on optimal dynamic programming algorithms for the single-agent version of the problem, optimal algorithms for the multiagent case have been elusive. The main contribution of this paper is an optimal policy iteration algorithm for solving DEC-POMDPs. The algorithm uses stochastic finite-state controllers to represent policies. The solution can include a correlation device, which allows agents to correlate their actions without communicating. This approach alternates between expanding the controller and performing value-preserving transformations, which modify the controller without sacrificing value. We present two efficient value-preserving transformations: one can reduce the size of the controller and the other can improve its value while keeping the size fixed. Empirical results demonstrate the usefulness of value-preserving transformations in increasing value while keeping controller size to a minimum. To broaden the applicability of the approach, we also present a heuristic version of the policy iteration algorithm, which sacrifices convergence to optimality. This algorithm further reduces the size of the controllers at each step by assuming that probability distributions over the other agents actions are known. While this assumption may not hold in general, it helps produce higher quality solutions in our test problems.

A Heuristic Search Approach to Planning with Continuous Resources in Stochastic Domains

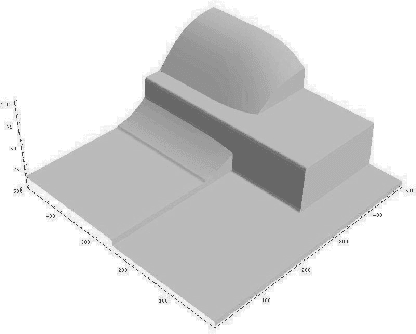
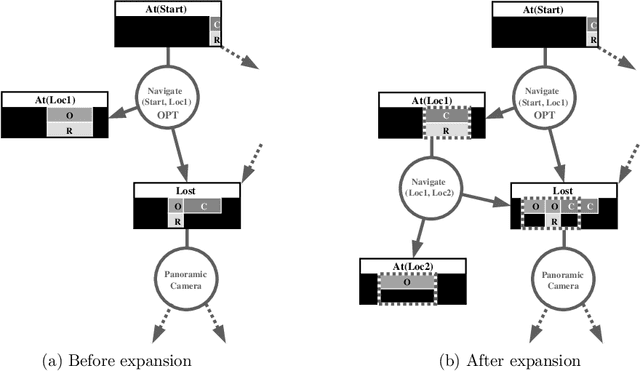
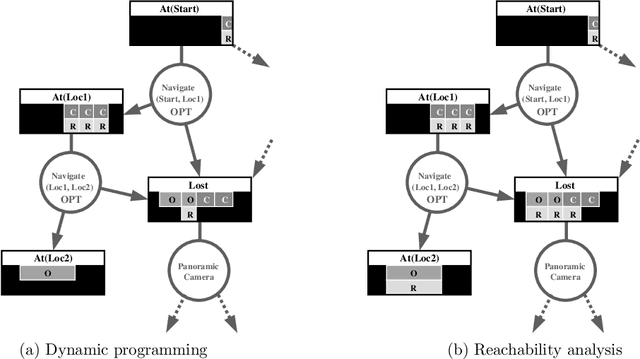
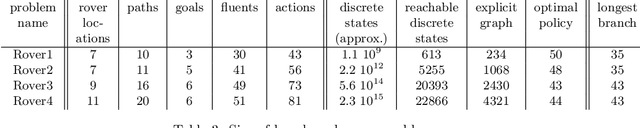
We consider the problem of optimal planning in stochastic domains with resource constraints, where the resources are continuous and the choice of action at each step depends on resource availability. We introduce the HAO* algorithm, a generalization of the AO* algorithm that performs search in a hybrid state space that is modeled using both discrete and continuous state variables, where the continuous variables represent monotonic resources. Like other heuristic search algorithms, HAO* leverages knowledge of the start state and an admissible heuristic to focus computational effort on those parts of the state space that could be reached from the start state by following an optimal policy. We show that this approach is especially effective when resource constraints limit how much of the state space is reachable. Experimental results demonstrate its effectiveness in the domain that motivates our research: automated planning for planetary exploration rovers.

Solving Limited-Memory Influence Diagrams Using Branch-and-Bound Search

A limited-memory influence diagram (LIMID) generalizes a traditional influence diagram by relaxing the assumptions of regularity and no-forgetting, allowing a wider range of decision problems to be modeled. Algorithms for solving traditional influence diagrams are not easily generalized to solve LIMIDs, however, and only recently have exact algorithms for solving LIMIDs been developed. In this paper, we introduce an exact algorithm for solving LIMIDs that is based on branch-and-bound search. Our approach is related to the approach of solving an influence diagram by converting it to an equivalent decision tree, with the difference that the LIMID is converted to a much smaller decision graph that can be searched more efficiently.

Solving POMDPs by Searching in Policy Space

Most algorithms for solving POMDPs iteratively improve a value function that implicitly represents a policy and are said to search in value function space. This paper presents an approach to solving POMDPs that represents a policy explicitly as a finite-state controller and iteratively improves the controller by search in policy space. Two related algorithms illustrate this approach. The first is a policy iteration algorithm that can outperform value iteration in solving infinitehorizon POMDPs. It provides the foundation for a new heuristic search algorithm that promises further speedup by focusing computational effort on regions of the problem space that are reachable, or likely to be reached, from a start state.

Symbolic Generalization for On-line Planning

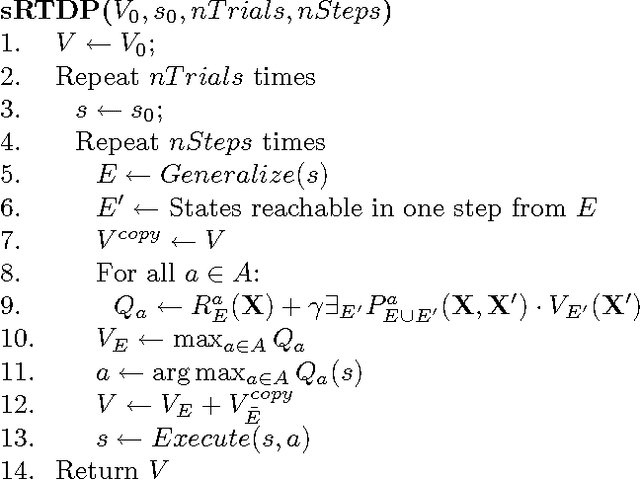
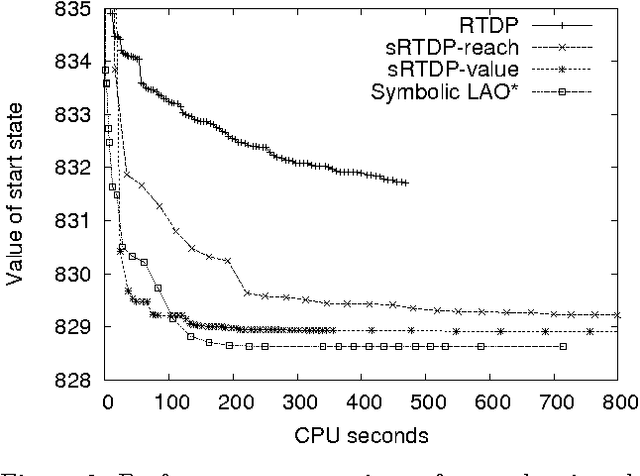
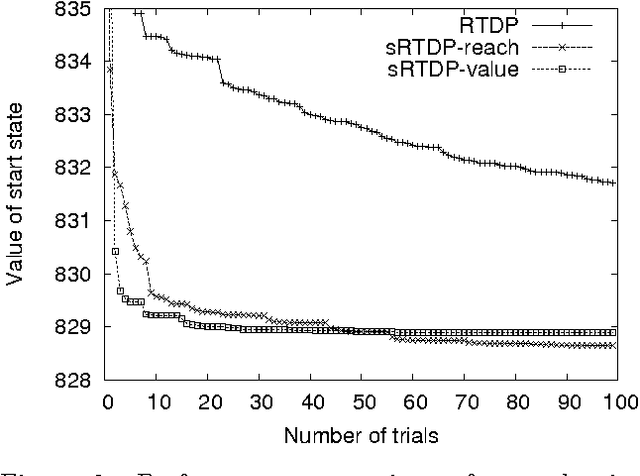
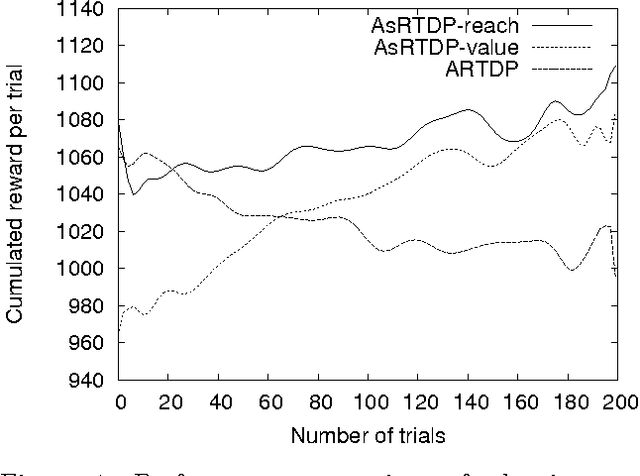
Symbolic representations have been used successfully in off-line planning algorithms for Markov decision processes. We show that they can also improve the performance of on-line planners. In addition to reducing computation time, symbolic generalization can reduce the amount of costly real-world interactions required for convergence. We introduce Symbolic Real-Time Dynamic Programming (or sRTDP), an extension of RTDP. After each step of on-line interaction with an environment, sRTDP uses symbolic model-checking techniques to generalizes its experience by updating a group of states rather than a single state. We examine two heuristic approaches to dynamic grouping of states and show that they accelerate the planning process significantly in terms of both CPU time and the number of steps of interaction with the environment.

Sparse Stochastic Finite-State Controllers for POMDPs

Bounded policy iteration is an approach to solving infinite-horizon POMDPs that represents policies as stochastic finite-state controllers and iteratively improves a controller by adjusting the parameters of each node using linear programming. In the original algorithm, the size of the linear programs, and thus the complexity of policy improvement, depends on the number of parameters of each node, which grows with the size of the controller. But in practice, the number of parameters of a node with non-zero values is often very small, and does not grow with the size of the controller. Based on this observation, we develop a version of bounded policy iteration that leverages the sparse structure of a stochastic finite-state controller. In each iteration, it improves a policy by the same amount as the original algorithm, but with much better scalability.

Solving Multistage Influence Diagrams using Branch-and-Bound Search

A branch-and-bound approach to solving influ- ence diagrams has been previously proposed in the literature, but appears to have never been implemented and evaluated - apparently due to the difficulties of computing effective bounds for the branch-and-bound search. In this paper, we describe how to efficiently compute effective bounds, and we develop a practical implementa- tion of depth-first branch-and-bound search for influence diagram evaluation that outperforms existing methods for solving influence diagrams with multiple stages.

Suboptimality Bounds for Stochastic Shortest Path Problems

We consider how to use the Bellman residual of the dynamic programming operator to compute suboptimality bounds for solutions to stochastic shortest path problems. Such bounds have been previously established only in the special case that "all policies are proper," in which case the dynamic programming operator is known to be a contraction, and have been shown to be easily computable only in the more limited special case of discounting. Under the condition that transition costs are positive, we show that suboptimality bounds can be easily computed even when not all policies are proper. In the general case when there are no restrictions on transition costs, the analysis is more complex. But we present preliminary results that show such bounds are possible.

Improving the Scalability of Optimal Bayesian Network Learning with External-Memory Frontier Breadth-First Branch and Bound Search

Previous work has shown that the problem of learning the optimal structure of a Bayesian network can be formulated as a shortest path finding problem in a graph and solved using A* search. In this paper, we improve the scalability of this approach by developing a memory-efficient heuristic search algorithm for learning the structure of a Bayesian network. Instead of using A*, we propose a frontier breadth-first branch and bound search that leverages the layered structure of the search graph of this problem so that no more than two layers of the graph, plus solution reconstruction information, need to be stored in memory at a time. To further improve scalability, the algorithm stores most of the graph in external memory, such as hard disk, when it does not fit in RAM. Experimental results show that the resulting algorithm solves significantly larger problems than the current state of the art.