Integrating Planning and Execution in Stochastic Domains

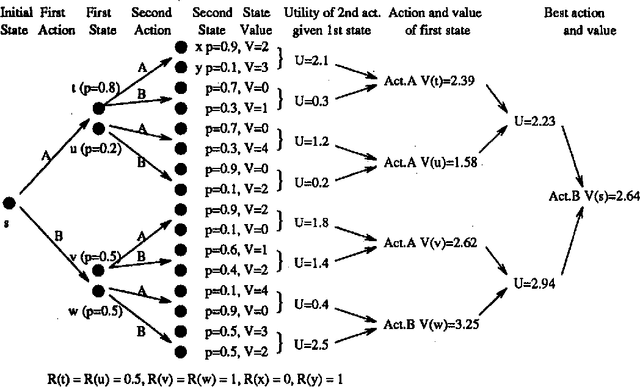
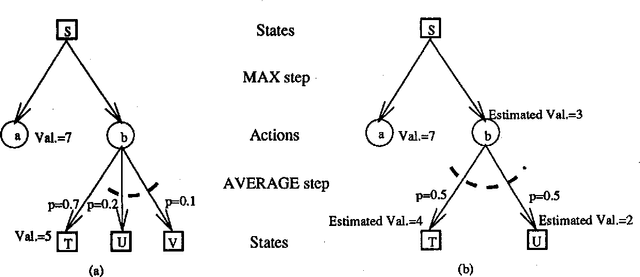
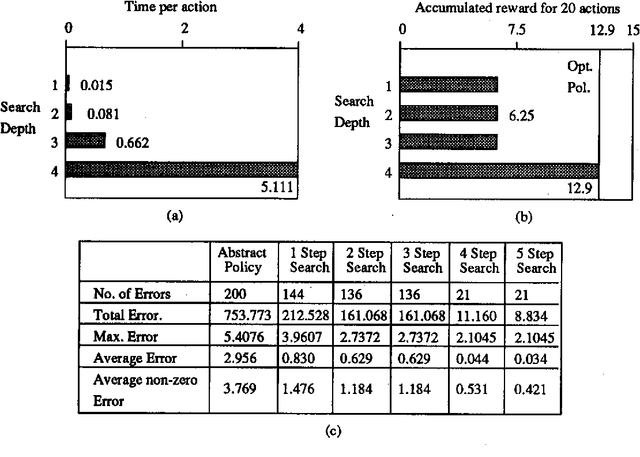
We investigate planning in time-critical domains represented as Markov Decision Processes, showing that search based techniques can be a very powerful method for finding close to optimal plans. To reduce the computational cost of planning in these domains, we execute actions as we construct the plan, and sacrifice optimality by searching to a fixed depth and using a heuristic function to estimate the value of states. Although this paper concentrates on the search algorithm, we also discuss ways of constructing heuristic functions suitable for this approach. Our results show that by interleaving search and execution, close to optimal policies can be found without the computational requirements of other approaches.

Model-Based Bayesian Exploration

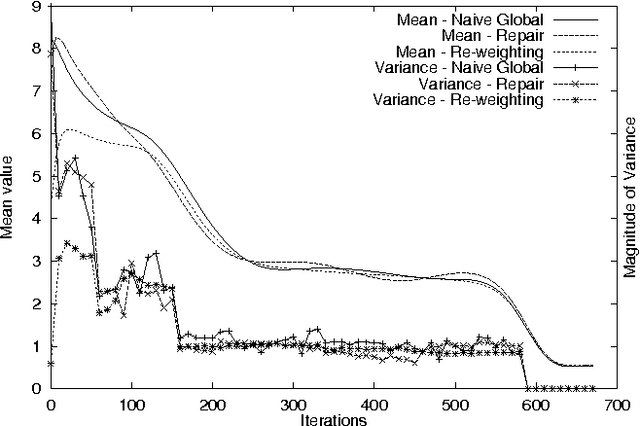
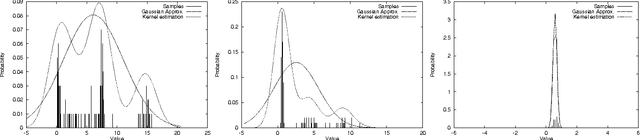
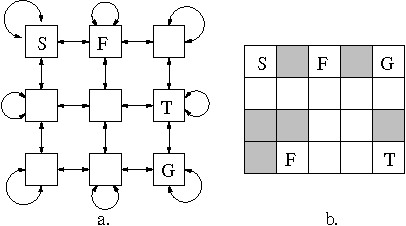
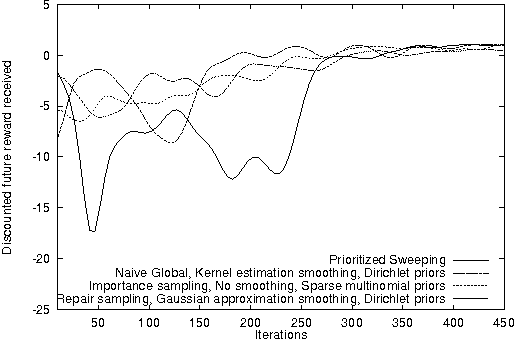
Reinforcement learning systems are often concerned with balancing exploration of untested actions against exploitation of actions that are known to be good. The benefit of exploration can be estimated using the classical notion of Value of Information - the expected improvement in future decision quality arising from the information acquired by exploration. Estimating this quantity requires an assessment of the agent's uncertainty about its current value estimates for states. In this paper we investigate ways of representing and reasoning about this uncertainty in algorithms where the system attempts to learn a model of its environment. We explicitly represent uncertainty about the parameters of the model and build probability distributions over Q-values based on these. These distributions are used to compute a myopic approximation to the value of information for each action and hence to select the action that best balances exploration and exploitation.

Planning under Continuous Time and Resource Uncertainty: A Challenge for AI

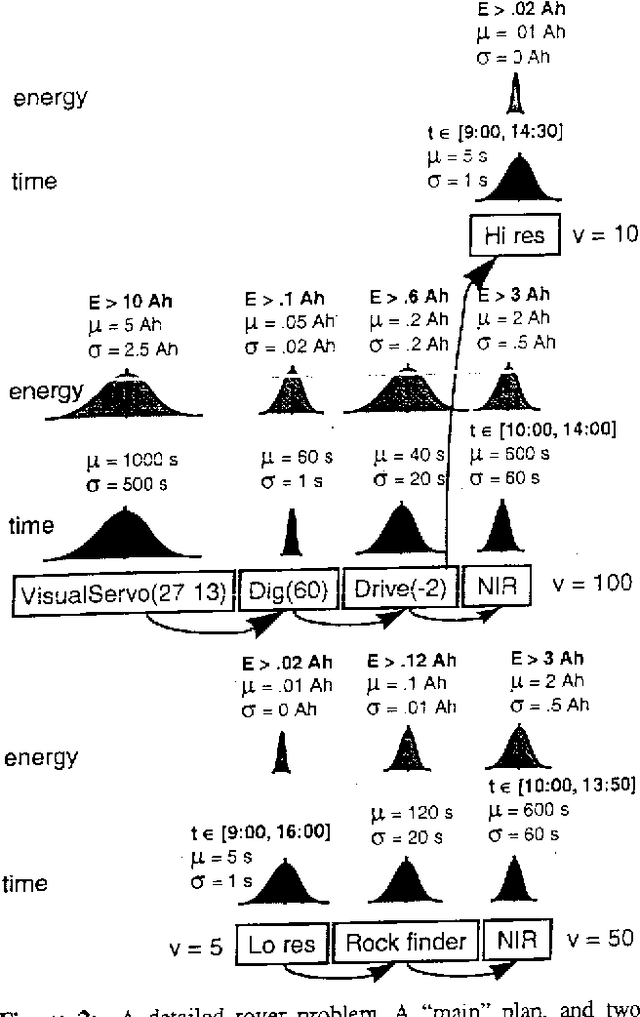
We outline a class of problems, typical of Mars rover operations, that are problematic for current methods of planning under uncertainty. The existing methods fail because they suffer from one or more of the following limitations: 1) they rely on very simple models of actions and time, 2) they assume that uncertainty is manifested in discrete action outcomes, 3) they are only practical for very small problems. For many real world problems, these assumptions fail to hold. In particular, when planning the activities for a Mars rover, none of the above assumptions is valid: 1) actions can be concurrent and have differing durations, 2) there is uncertainty concerning action durations and consumption of continuous resources like power, and 3) typical daily plans involve on the order of a hundred actions. This class of problems may be of particular interest to the UAI community because both classical and decision-theoretic planning techniques may be useful in solving it. We describe the rover problem, discuss previous work on planning under uncertainty, and present a detailed, but very small, example illustrating some of the difficulties of finding good plans.

Dynamic Programming for Structured Continuous Markov Decision Problems

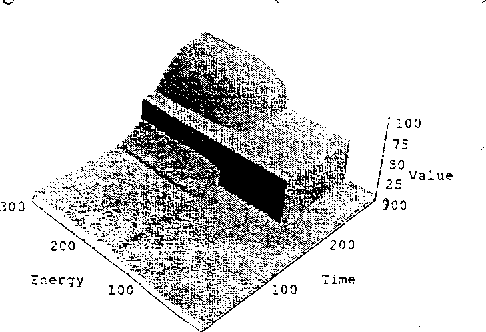
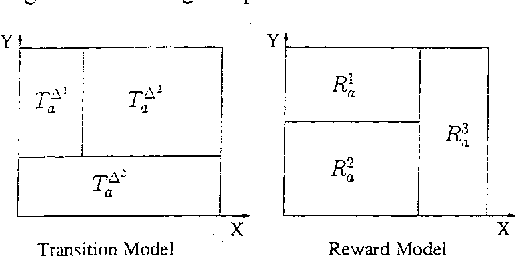
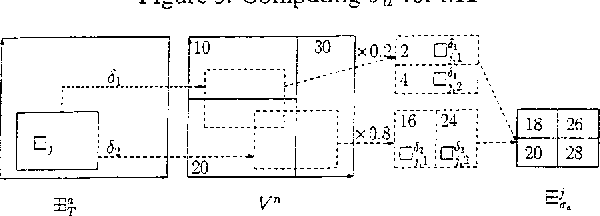
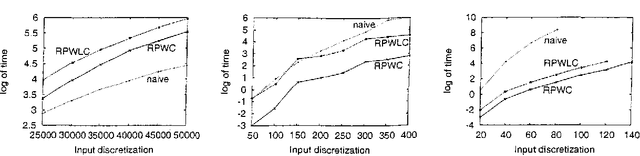
We describe an approach for exploiting structure in Markov Decision Processes with continuous state variables. At each step of the dynamic programming, the state space is dynamically partitioned into regions where the value function is the same throughout the region. We first describe the algorithm for piecewise constant representations. We then extend it to piecewise linear representations, using techniques from POMDPs to represent and reason about linear surfaces efficiently. We show that for complex, structured problems, our approach exploits the natural structure so that optimal solutions can be computed efficiently.