Integrating Planning and Execution in Stochastic Domains
Paper and Code
Feb 27, 2013
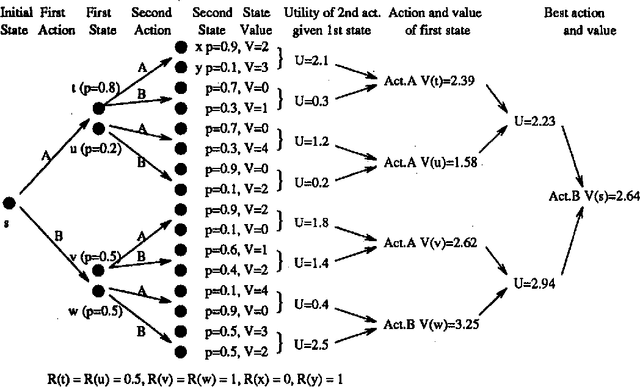
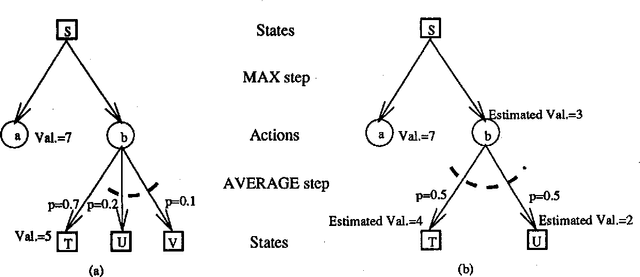
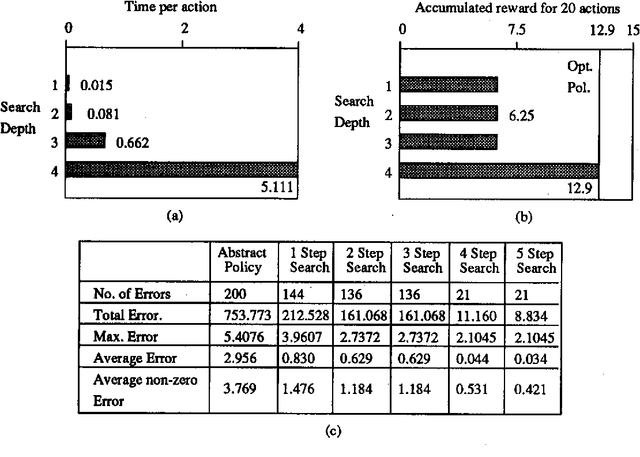
We investigate planning in time-critical domains represented as Markov Decision Processes, showing that search based techniques can be a very powerful method for finding close to optimal plans. To reduce the computational cost of planning in these domains, we execute actions as we construct the plan, and sacrifice optimality by searching to a fixed depth and using a heuristic function to estimate the value of states. Although this paper concentrates on the search algorithm, we also discuss ways of constructing heuristic functions suitable for this approach. Our results show that by interleaving search and execution, close to optimal policies can be found without the computational requirements of other approaches.
* Appears in Proceedings of the Tenth Conference on Uncertainty in
Artificial Intelligence (UAI1994)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge