Probabilistic Causal Reasoning

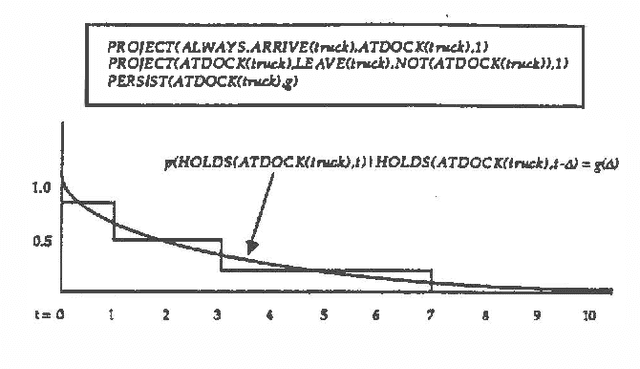
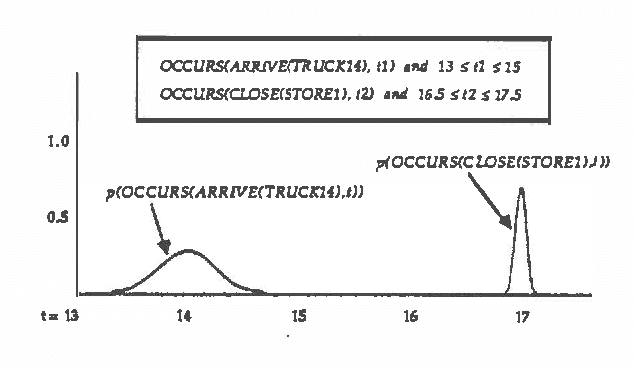
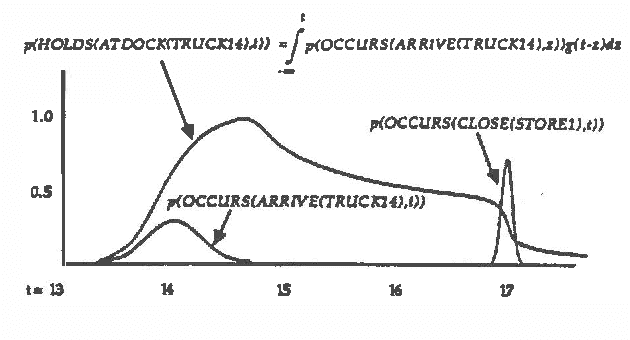
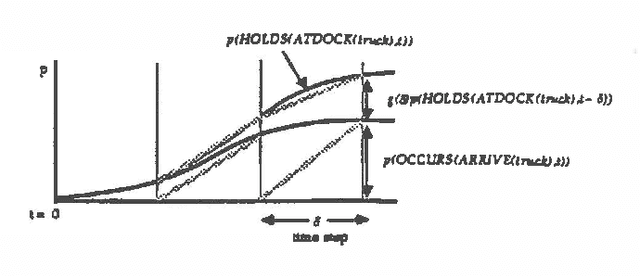
Predicting the future is an important component of decision making. In most situations, however, there is not enough information to make accurate predictions. In this paper, we develop a theory of causal reasoning for predictive inference under uncertainty. We emphasize a common type of prediction that involves reasoning about persistence: whether or not a proposition once made true remains true at some later time. We provide a decision procedure with a polynomial-time algorithm for determining the probability of the possible consequences of a set events and initial conditions. The integration of simple probability theory with temporal projection enables us to circumvent problems that nonmonotonic temporal reasoning schemes have in dealing with persistence. The ideas in this paper have been implemented in a prototype system that refines a database of causal rules in the course of applying those rules to construct and carry out plans in a manufacturing domain.

Map Learning with Indistinguishable Locations

Nearly all spatial reasoning problems involve uncertainty of one sort or another. Uncertainty arises due to the inaccuracies of sensors used in measuring distances and angles. We refer to this as directional uncertainty. Uncertainty also arises in combining spatial information when one location is mistakenly identified with another. We refer to this as recognition uncertainty. Most problems in constructing spatial representations (maps) for the purpose of navigation involve both directional and recognition uncertainty. In this paper, we show that a particular class of spatial reasoning problems involving the construction of representations of large-scale space can be solved efficiently even in the presence of directional and recognition uncertainty. We pay particular attention to the problems that arise due to recognition uncertainty.

Deliberation Scheduling for Time-Critical Sequential Decision Making

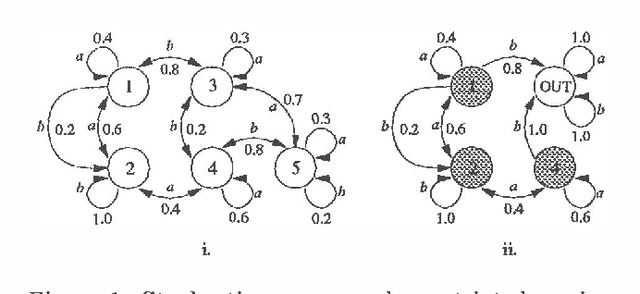
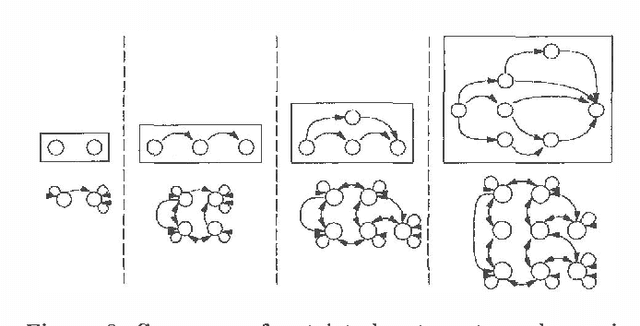
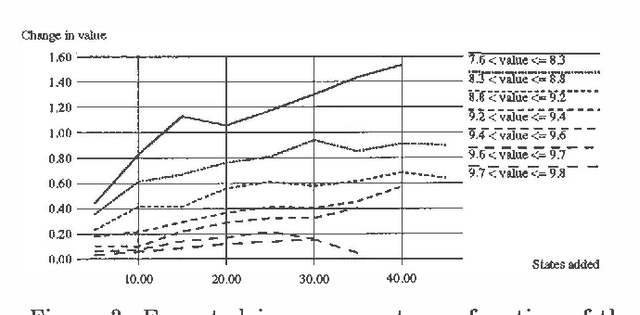
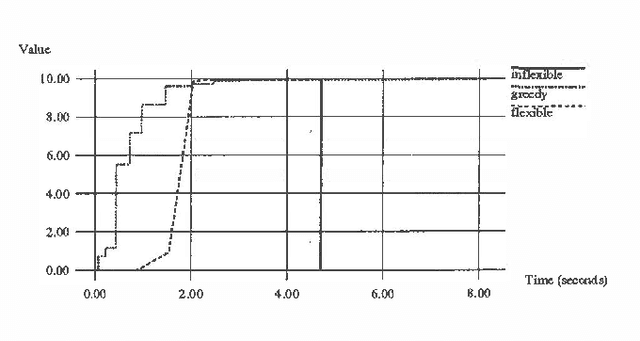
We describe a method for time-critical decision making involving sequential tasks and stochastic processes. The method employs several iterative refinement routines for solving different aspects of the decision making problem. This paper concentrates on the meta-level control problem of deliberation scheduling, allocating computational resources to these routines. We provide different models corresponding to optimization problems that capture the different circumstances and computational strategies for decision making under time constraints. We consider precursor models in which all decision making is performed prior to execution and recurrent models in which decision making is performed in parallel with execution, accounting for the states observed during execution and anticipating future states. We describe algorithms for precursor and recurrent models and provide the results of our empirical investigations to date.

On the Complexity of Solving Markov Decision Problems

Markov decision problems (MDPs) provide the foundations for a number of problems of interest to AI researchers studying automated planning and reinforcement learning. In this paper, we summarize results regarding the complexity of solving MDPs and the running time of MDP solution algorithms. We argue that, although MDPs can be solved efficiently in theory, more study is needed to reveal practical algorithms for solving large problems quickly. To encourage future research, we sketch some alternative methods of analysis that rely on the structure of MDPs.

Model Reduction Techniques for Computing Approximately Optimal Solutions for Markov Decision Processes

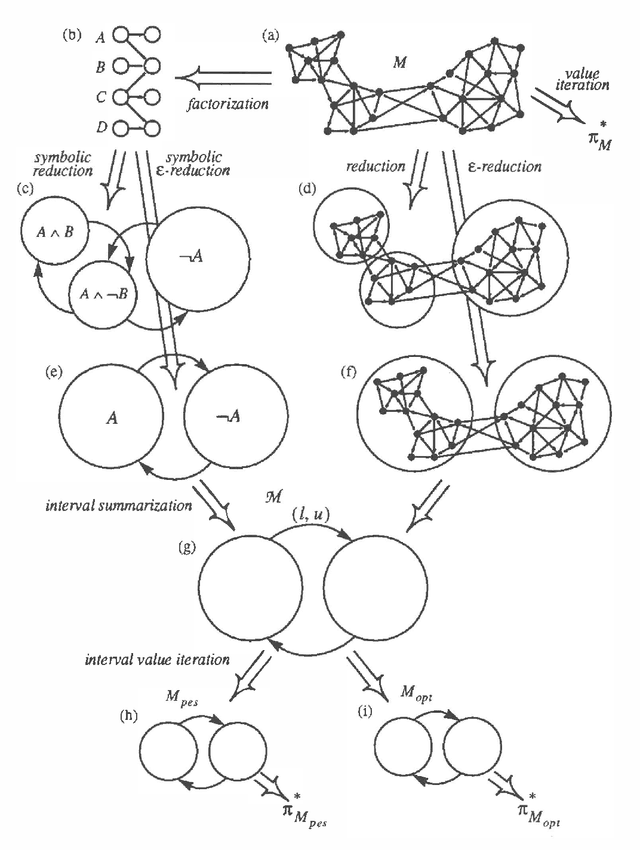
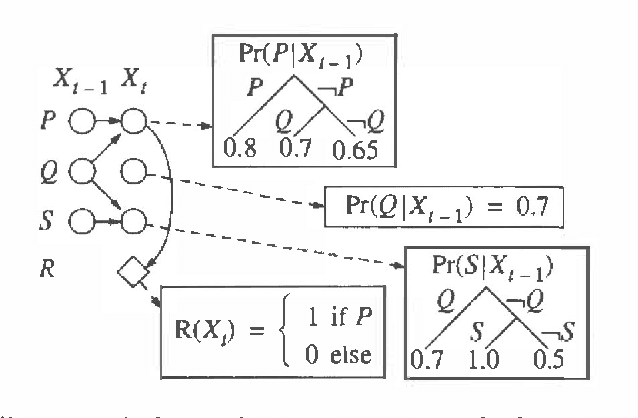
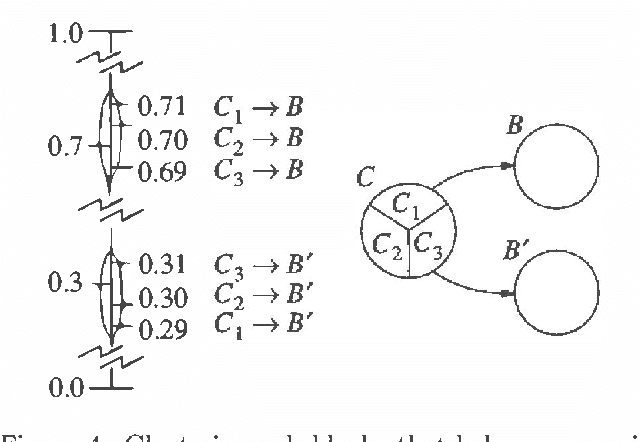
We present a method for solving implicit (factored) Markov decision processes (MDPs) with very large state spaces. We introduce a property of state space partitions which we call epsilon-homogeneity. Intuitively, an epsilon-homogeneous partition groups together states that behave approximately the same under all or some subset of policies. Borrowing from recent work on model minimization in computer-aided software verification, we present an algorithm that takes a factored representation of an MDP and an 0<=epsilon<=1 and computes a factored epsilon-homogeneous partition of the state space. This partition defines a family of related MDPs - those MDPs with state space equal to the blocks of the partition, and transition probabilities "approximately" like those of any (original MDP) state in the source block. To formally study such families of MDPs, we introduce the new notion of a "bounded parameter MDP" (BMDP), which is a family of (traditional) MDPs defined by specifying upper and lower bounds on the transition probabilities and rewards. We describe algorithms that operate on BMDPs to find policies that are approximately optimal with respect to the original MDP. In combination, our method for reducing a large implicit MDP to a possibly much smaller BMDP using an epsilon-homogeneous partition, and our methods for selecting actions in BMDPs constitute a new approach for analyzing large implicit MDPs. Among its advantages, this new approach provides insight into existing algorithms to solving implicit MDPs, provides useful connections to work in automata theory and model minimization, and suggests methods, which involve varying epsilon, to trade time and space (specifically in terms of the size of the corresponding state space) for solution quality.

Hierarchical Solution of Markov Decision Processes using Macro-actions

We investigate the use of temporally abstract actions, or macro-actions, in the solution of Markov decision processes. Unlike current models that combine both primitive actions and macro-actions and leave the state space unchanged, we propose a hierarchical model (using an abstract MDP) that works with macro-actions only, and that significantly reduces the size of the state space. This is achieved by treating macroactions as local policies that act in certain regions of state space, and by restricting states in the abstract MDP to those at the boundaries of regions. The abstract MDP approximates the original and can be solved more efficiently. We discuss several ways in which macro-actions can be generated to ensure good solution quality. Finally, we consider ways in which macro-actions can be reused to solve multiple, related MDPs; and we show that this can justify the computational overhead of macro-action generation.

Exploiting Locality in Searching the Web

Published experiments on spidering the Web suggest that, given training data in the form of a (relatively small) subgraph of the Web containing a subset of a selected class of target pages, it is possible to conduct a directed search and find additional target pages significantly faster (with fewer page retrievals) than by performing a blind or uninformed random or systematic search, e.g., breadth-first search. If true, this claim motivates a number of practical applications. Unfortunately, these experiments were carried out in specialized domains or under conditions that are difficult to replicate. We present and apply an experimental framework designed to reexamine and resolve the basic claims of the earlier work, so that the supporting experiments can be replicated and built upon. We provide high-performance tools for building experimental spiders, make use of the ground truth and static nature of the WT10g TREC Web corpus, and rely on simple well understand machine learning techniques to conduct our experiments. In this paper, we describe the basic framework, motivate the experimental design, and report on our findings supporting and qualifying the conclusions of the earlier research.