Probabilistic Causal Reasoning

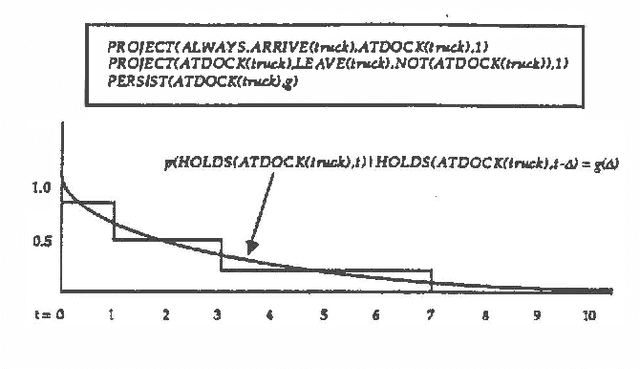
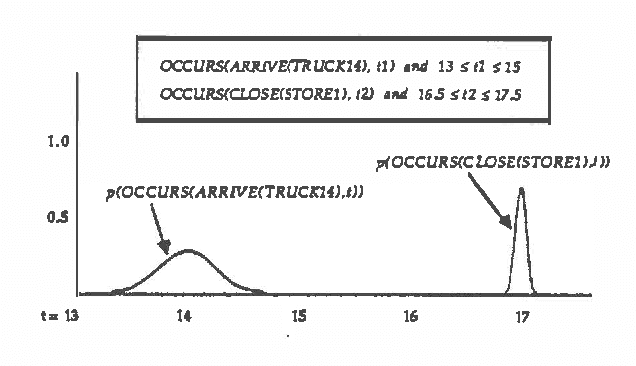
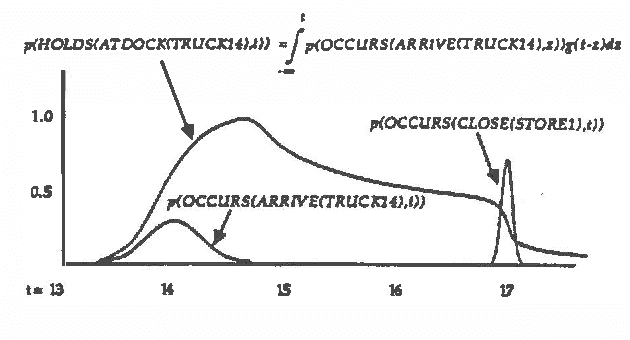
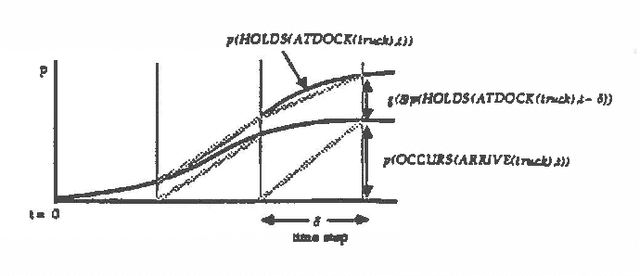
Predicting the future is an important component of decision making. In most situations, however, there is not enough information to make accurate predictions. In this paper, we develop a theory of causal reasoning for predictive inference under uncertainty. We emphasize a common type of prediction that involves reasoning about persistence: whether or not a proposition once made true remains true at some later time. We provide a decision procedure with a polynomial-time algorithm for determining the probability of the possible consequences of a set events and initial conditions. The integration of simple probability theory with temporal projection enables us to circumvent problems that nonmonotonic temporal reasoning schemes have in dealing with persistence. The ideas in this paper have been implemented in a prototype system that refines a database of causal rules in the course of applying those rules to construct and carry out plans in a manufacturing domain.

Reducing Uncertainty in Navigation and Exploration

A significant problem in designing mobile robot control systems involves coping with the uncertainty that arises in moving about in an unknown or partially unknown environment and relying on noisy or ambiguous sensor data to acquire knowledge about that environment. We describe a control system that chooses what activity to engage in next on the basis of expectations about how the information re- turned as a result of a given activity will improve 2 its knowledge about the spatial layout of its environment. Certain of the higher-level components of the control system are specified in terms of probabilistic decision models whose output is used to mediate the behavior of lower-level control components responsible for movement and sensing.

Stochastic Simulation Algorithms for Dynamic Probabilistic Networks

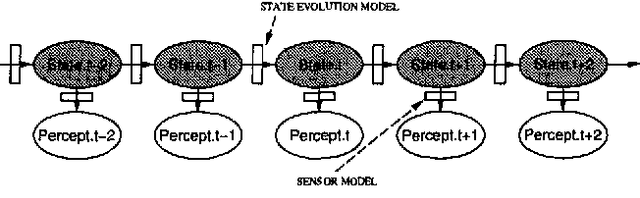
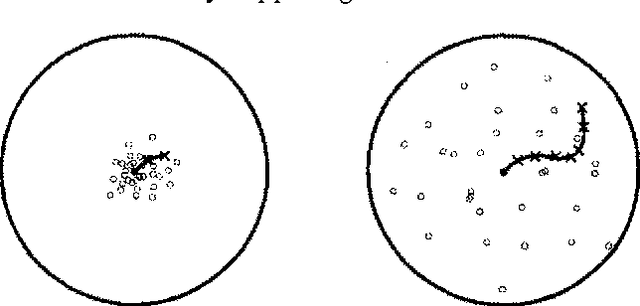
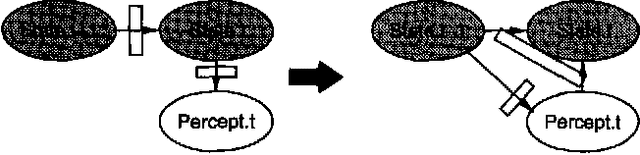
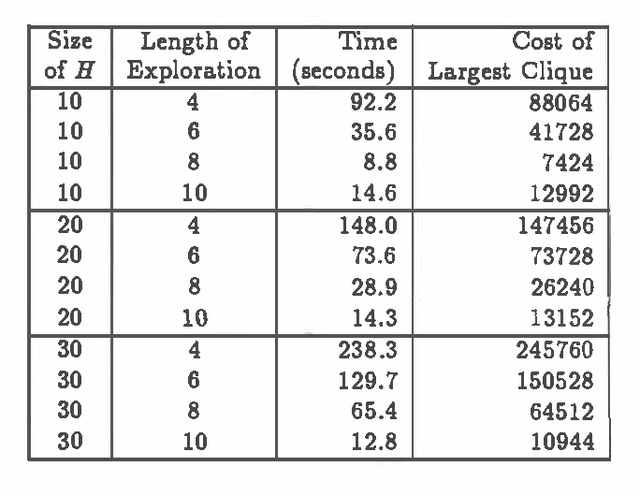
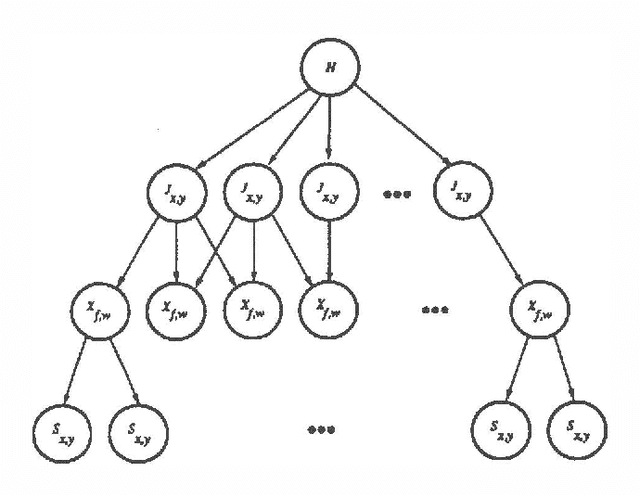
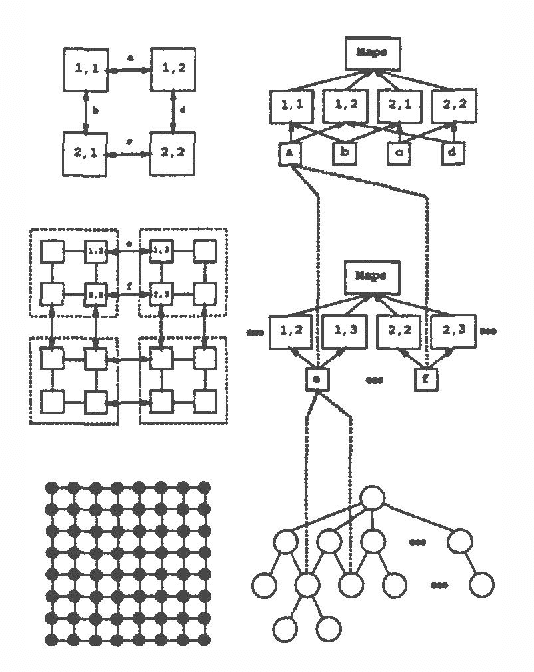
Stochastic simulation algorithms such as likelihood weighting often give fast, accurate approximations to posterior probabilities in probabilistic networks, and are the methods of choice for very large networks. Unfortunately, the special characteristics of dynamic probabilistic networks (DPNs), which are used to represent stochastic temporal processes, mean that standard simulation algorithms perform very poorly. In essence, the simulation trials diverge further and further from reality as the process is observed over time. In this paper, we present simulation algorithms that use the evidence observed at each time step to push the set of trials back towards reality. The first algorithm, "evidence reversal" (ER) restructures each time slice of the DPN so that the evidence nodes for the slice become ancestors of the state variables. The second algorithm, called "survival of the fittest" sampling (SOF), "repopulates" the set of trials at each time step using a stochastic reproduction rate weighted by the likelihood of the evidence according to each trial. We compare the performance of each algorithm with likelihood weighting on the original network, and also investigate the benefits of combining the ER and SOF methods. The ER/SOF combination appears to maintain bounded error independent of the number of time steps in the simulation.