Stochastic Simulation Algorithms for Dynamic Probabilistic Networks
Paper and Code
Feb 20, 2013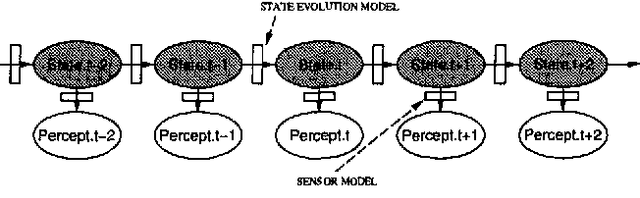

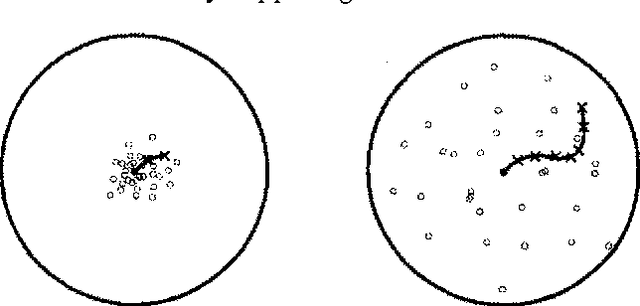
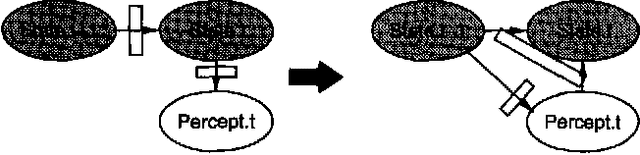
Stochastic simulation algorithms such as likelihood weighting often give fast, accurate approximations to posterior probabilities in probabilistic networks, and are the methods of choice for very large networks. Unfortunately, the special characteristics of dynamic probabilistic networks (DPNs), which are used to represent stochastic temporal processes, mean that standard simulation algorithms perform very poorly. In essence, the simulation trials diverge further and further from reality as the process is observed over time. In this paper, we present simulation algorithms that use the evidence observed at each time step to push the set of trials back towards reality. The first algorithm, "evidence reversal" (ER) restructures each time slice of the DPN so that the evidence nodes for the slice become ancestors of the state variables. The second algorithm, called "survival of the fittest" sampling (SOF), "repopulates" the set of trials at each time step using a stochastic reproduction rate weighted by the likelihood of the evidence according to each trial. We compare the performance of each algorithm with likelihood weighting on the original network, and also investigate the benefits of combining the ER and SOF methods. The ER/SOF combination appears to maintain bounded error independent of the number of time steps in the simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge