Automatic Induction of Bellman-Error Features for Probabilistic Planning

Domain-specific features are important in representing problem structure throughout machine learning and decision-theoretic planning. In planning, once state features are provided, domain-independent algorithms such as approximate value iteration can learn weighted combinations of those features that often perform well as heuristic estimates of state value (e.g., distance to the goal). Successful applications in real-world domains often require features crafted by human experts. Here, we propose automatic processes for learning useful domain-specific feature sets with little or no human intervention. Our methods select and add features that describe state-space regions of high inconsistency in the Bellman equation (statewise Bellman error) during approximate value iteration. Our method can be applied using any real-valued-feature hypothesis space and corresponding learning method for selecting features from training sets of state-value pairs. We evaluate the method with hypothesis spaces defined by both relational and propositional feature languages, using nine probabilistic planning domains. We show that approximate value iteration using a relational feature space performs at the state-of-the-art in domain-independent stochastic relational planning. Our method provides the first domain-independent approach that plays Tetris successfully (without human-engineered features).

Model Reduction Techniques for Computing Approximately Optimal Solutions for Markov Decision Processes

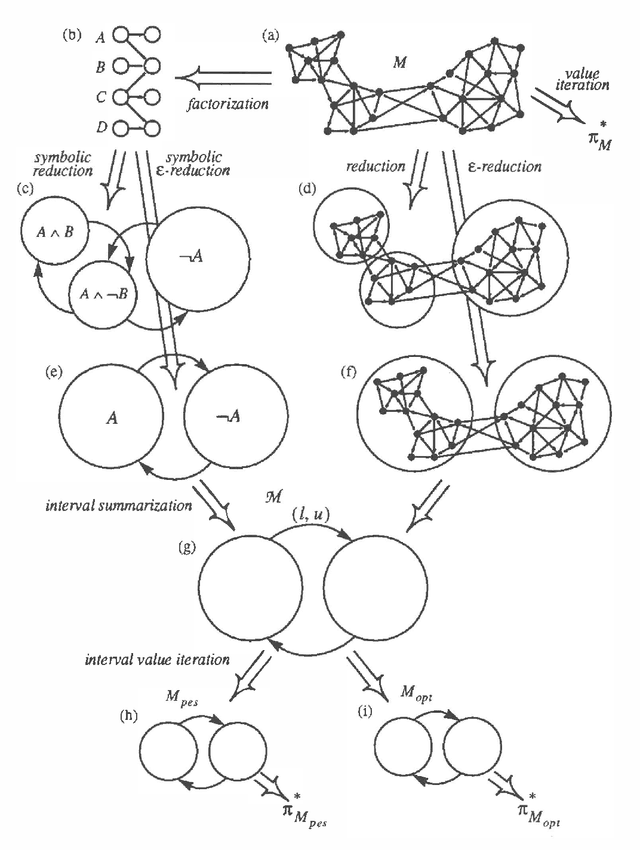
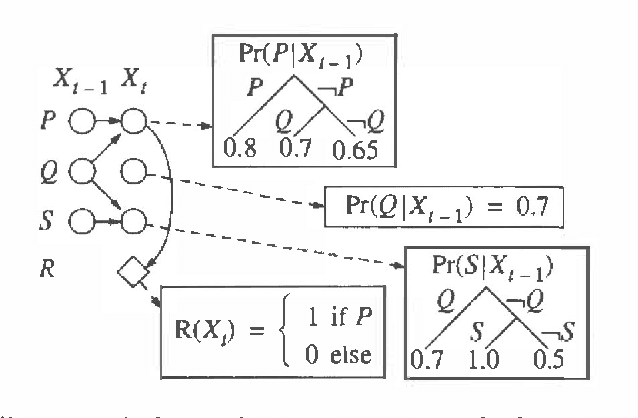
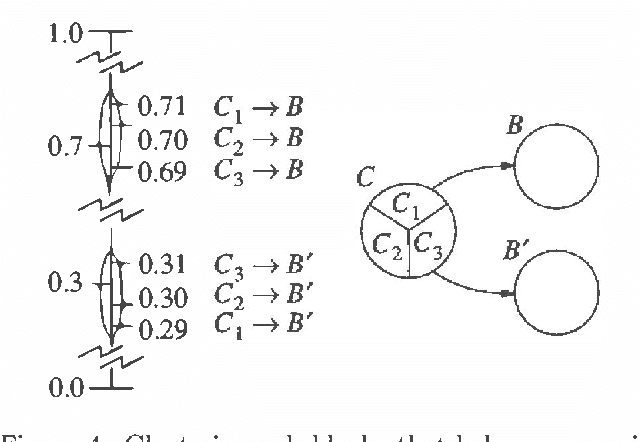
We present a method for solving implicit (factored) Markov decision processes (MDPs) with very large state spaces. We introduce a property of state space partitions which we call epsilon-homogeneity. Intuitively, an epsilon-homogeneous partition groups together states that behave approximately the same under all or some subset of policies. Borrowing from recent work on model minimization in computer-aided software verification, we present an algorithm that takes a factored representation of an MDP and an 0<=epsilon<=1 and computes a factored epsilon-homogeneous partition of the state space. This partition defines a family of related MDPs - those MDPs with state space equal to the blocks of the partition, and transition probabilities "approximately" like those of any (original MDP) state in the source block. To formally study such families of MDPs, we introduce the new notion of a "bounded parameter MDP" (BMDP), which is a family of (traditional) MDPs defined by specifying upper and lower bounds on the transition probabilities and rewards. We describe algorithms that operate on BMDPs to find policies that are approximately optimal with respect to the original MDP. In combination, our method for reducing a large implicit MDP to a possibly much smaller BMDP using an epsilon-homogeneous partition, and our methods for selecting actions in BMDPs constitute a new approach for analyzing large implicit MDPs. Among its advantages, this new approach provides insight into existing algorithms to solving implicit MDPs, provides useful connections to work in automata theory and model minimization, and suggests methods, which involve varying epsilon, to trade time and space (specifically in terms of the size of the corresponding state space) for solution quality.

Inductive Policy Selection for First-Order MDPs

We select policies for large Markov Decision Processes (MDPs) with compact first-order representations. We find policies that generalize well as the number of objects in the domain grows, potentially without bound. Existing dynamic-programming approaches based on flat, propositional, or first-order representations either are impractical here or do not naturally scale as the number of objects grows without bound. We implement and evaluate an alternative approach that induces first-order policies using training data constructed by solving small problem instances using PGraphplan (Blum & Langford, 1999). Our policies are represented as ensembles of decision lists, using a taxonomic concept language. This approach extends the work of Martin and Geffner (2000) to stochastic domains, ensemble learning, and a wider variety of problems. Empirically, we find "good" policies for several stochastic first-order MDPs that are beyond the scope of previous approaches. We also discuss the application of this work to the relational reinforcement-learning problem.

Estimating Densities with Non-Parametric Exponential Families

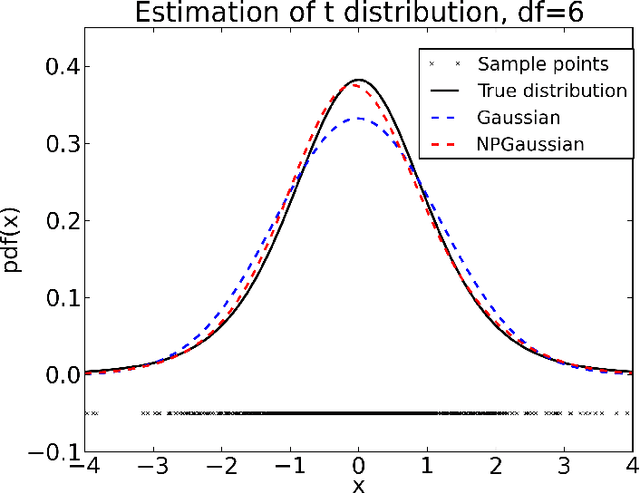
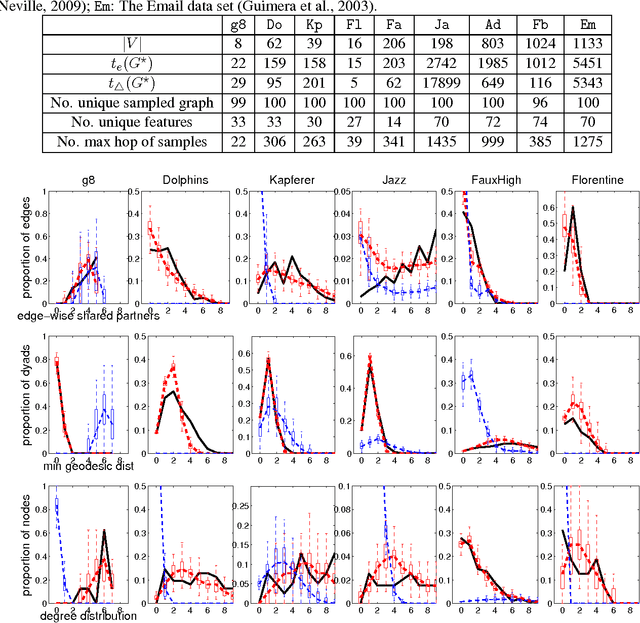
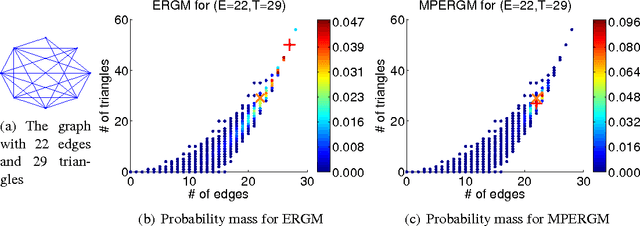
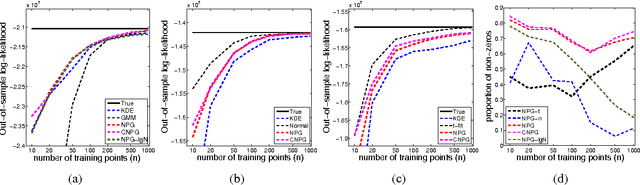
We propose a novel approach for density estimation with exponential families for the case when the true density may not fall within the chosen family. Our approach augments the sufficient statistics with features designed to accumulate probability mass in the neighborhood of the observed points, resulting in a non-parametric model similar to kernel density estimators. We show that under mild conditions, the resulting model uses only the sufficient statistics if the density is within the chosen exponential family, and asymptotically, it approximates densities outside of the chosen exponential family. Using the proposed approach, we modify the exponential random graph model, commonly used for modeling small-size graph distributions, to address the well-known issue of model degeneracy.

Polynomial-time Computation via Local Inference Relations

We consider the concept of a local set of inference rules. A local rule set can be automatically transformed into a rule set for which bottom-up evaluation terminates in polynomial time. The local-rule-set transformation gives polynomial-time evaluation strategies for a large variety of rule sets that cannot be given terminating evaluation strategies by any other known automatic technique. This paper discusses three new results. First, it is shown that every polynomial-time predicate can be defined by an (unstratified) local rule set. Second, a new machine-recognizable subclass of the local rule sets is identified. Finally we show that locality, as a property of rule sets, is undecidable in general.