Estimating Densities with Non-Parametric Exponential Families

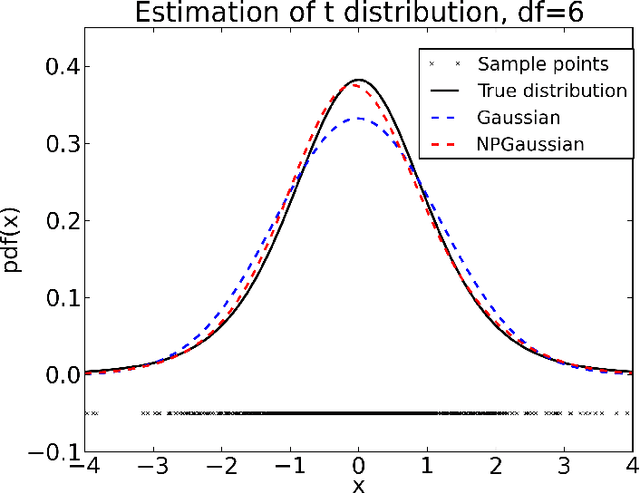
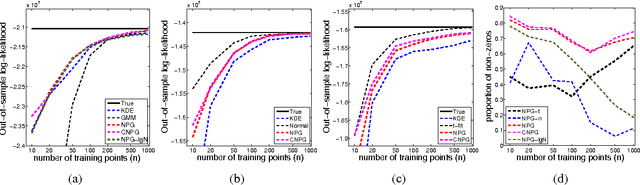
We propose a novel approach for density estimation with exponential families for the case when the true density may not fall within the chosen family. Our approach augments the sufficient statistics with features designed to accumulate probability mass in the neighborhood of the observed points, resulting in a non-parametric model similar to kernel density estimators. We show that under mild conditions, the resulting model uses only the sufficient statistics if the density is within the chosen exponential family, and asymptotically, it approximates densities outside of the chosen exponential family. Using the proposed approach, we modify the exponential random graph model, commonly used for modeling small-size graph distributions, to address the well-known issue of model degeneracy.

Conditional Chow-Liu Tree Structures for Modeling Discrete-Valued Vector Time Series

We consider the problem of modeling discrete-valued vector time series data using extensions of Chow-Liu tree models to capture both dependencies across time and dependencies across variables. Conditional Chow-Liu tree models are introduced, as an extension to standard Chow-Liu trees, for modeling conditional rather than joint densities. We describe learning algorithms for such models and show how they can be used to learn parsimonious representations for the output distributions in hidden Markov models. These models are applied to the important problem of simulating and forecasting daily precipitation occurrence for networks of rain stations. To demonstrate the effectiveness of the models, we compare their performance versus a number of alternatives using historical precipitation data from Southwestern Australia and the Western United States. We illustrate how the structure and parameters of the models can be used to provide an improved meteorological interpretation of such data.

Generating Similar Graphs From Spherical Features

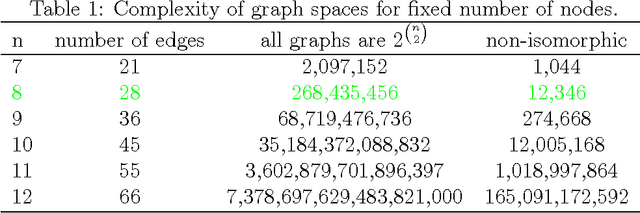
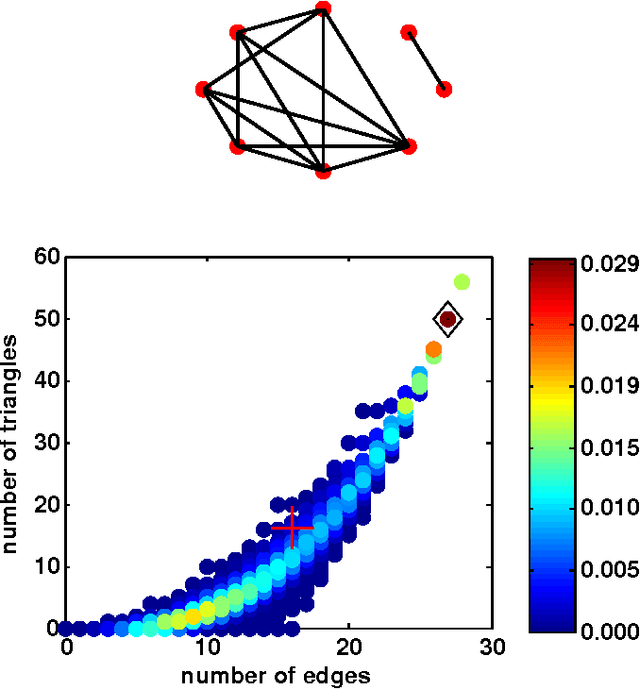
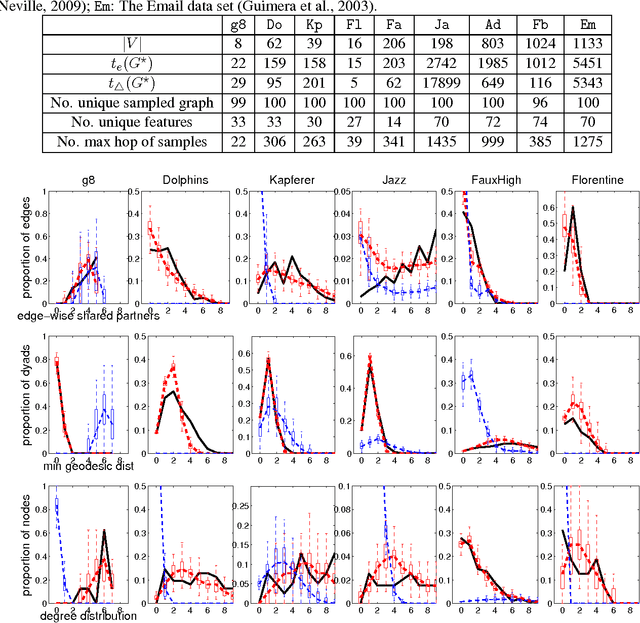
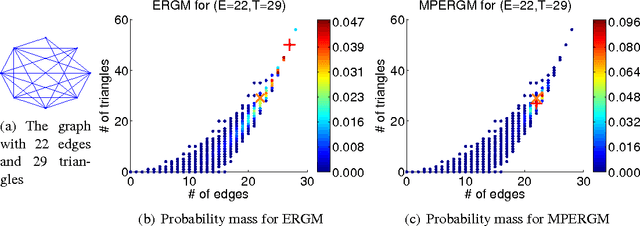
We propose a novel model for generating graphs similar to a given example graph. Unlike standard approaches that compute features of graphs in Euclidean space, our approach obtains features on a surface of a hypersphere. We then utilize a von Mises-Fisher distribution, an exponential family distribution on the surface of a hypersphere, to define a model over possible feature values. While our approach bears similarity to a popular exponential random graph model (ERGM), unlike ERGMs, it does not suffer from degeneracy, a situation when a significant probability mass is placed on unrealistic graphs. We propose a parameter estimation approach for our model, and a procedure for drawing samples from the distribution. We evaluate the performance of our approach both on the small domain of all 8-node graphs as well as larger real-world social networks.