Generating Similar Graphs From Spherical Features
Paper and Code
May 19, 2011
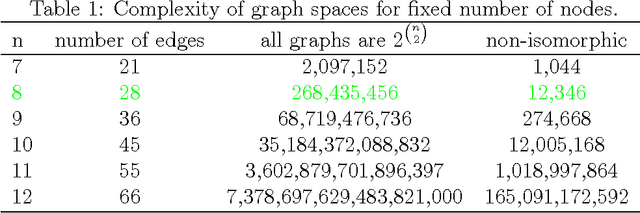

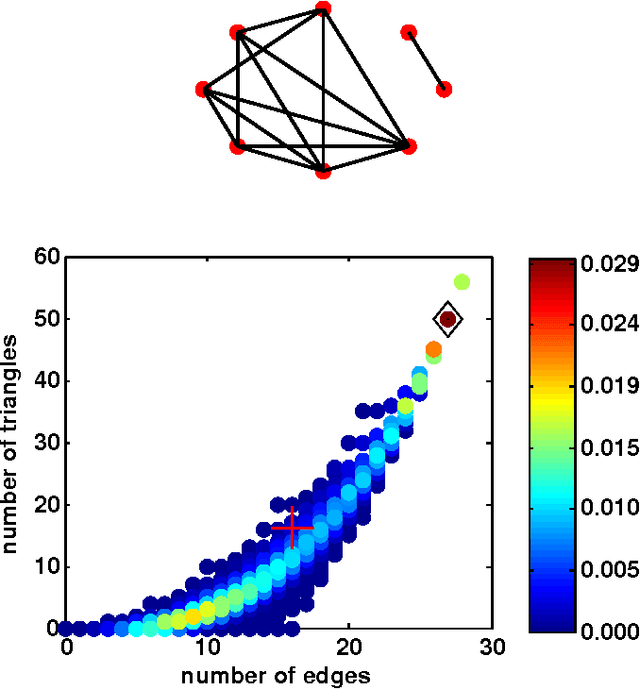
We propose a novel model for generating graphs similar to a given example graph. Unlike standard approaches that compute features of graphs in Euclidean space, our approach obtains features on a surface of a hypersphere. We then utilize a von Mises-Fisher distribution, an exponential family distribution on the surface of a hypersphere, to define a model over possible feature values. While our approach bears similarity to a popular exponential random graph model (ERGM), unlike ERGMs, it does not suffer from degeneracy, a situation when a significant probability mass is placed on unrealistic graphs. We propose a parameter estimation approach for our model, and a procedure for drawing samples from the distribution. We evaluate the performance of our approach both on the small domain of all 8-node graphs as well as larger real-world social networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge